本文主要是介绍【计算机视觉】Lecture 18:广义的立体视觉:对极几何,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
广义的立体视觉
主要思想:任何两张有重叠视图的图像,它们都可以被视为一对立体图像
我们只需要弄清楚这两个视图是如何关联的
视觉中一些最“漂亮”的数学问题是描述多个视图之间的几何关系。
回忆:对极约束(Epipolar Constraint)
重要的立体视觉概念:
给定左图像上的一个点,我们不必在整个右图像中搜索对应的点
“对极约束”将搜索空间缩小为一条一维的直线。
回顾:简单的立体视觉系统

回顾:对极约束

相应的特征被限制在共轭的极线上(在我们简单配置的例子中是位于同一行上的)
广义的立体视觉
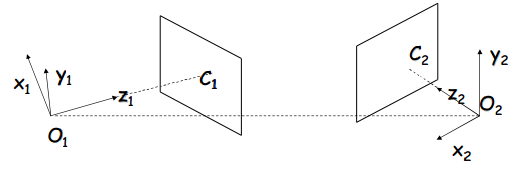
一般来说,相机可以通过任意变换(R,T)进行关联:对极矩阵
一般来说,相机内参可能是不同的,甚至是未知的:基础矩阵
对极几何
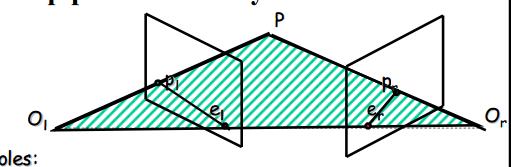
Ol, Or的连线与两个像平面的交点为el, er,称为极点(Epipoles)
Ol, Or, P三个点确定的平面称为极平面(Epipolar plane)
极平面与两个像平面的相交线plel,prer称为极线(Epipolar line)
对应的点在“共轭”的极线上:对极约束
可视化

光线到场景中的点

将线系在管脚上,并将焦点连接到场景点
对另一个观察者来说这会是什么样子?
从第二个观察者看到的光线

从第一个观察者看到的光线

对极几何

左边
极点:相机1所看到的相机2的位置。
右边
极点:相机2所看到的相机1的位置
对极几何

对应点位于共轭极线上
对极几何

共轭极线在图像上产生了广义的一维“扫描线”序列(类似于图像中行的传统扫描线序列)
极点不一定要在图像中

对极几何

Ol, Or的连线与两个像平面的交点为el, er,称为极点(Epipoles)
Ol, Or, P三个点确定的平面称为极平面(Epipolar plane)
极平面与两个像平面的相交线plel,prer称为极线(Epipolar line)
对应的点在“共轭”的极线上:对极约束
对极约束
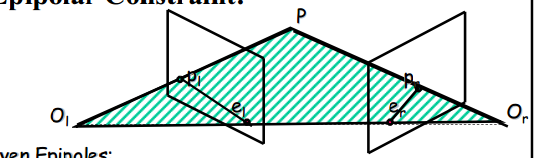
给定左特征点pl:
- 考虑它的极线:plel;
- 找到极平面Ol, pl, el;
- 极平面和右像平面的交叉线为右极线
- 在右极线上寻找pr
本质矩阵Essential Matrix

回忆:通过(R,T)将世界坐标系到相机坐标系的变换。在这里,我们从一个相机转变到另一个相机。
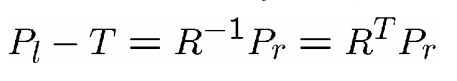
极线约束:Pl,T和Pl-T是共面的
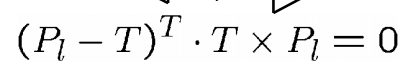
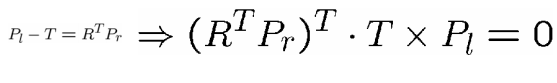
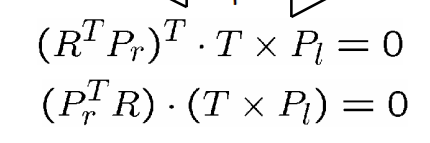
向量积作为矩阵乘法

本质矩阵

本质矩阵: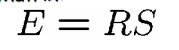
那么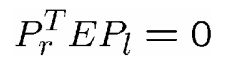
本质矩阵的性质

- rank为2
- 仅取决于外参(R和T)
这篇关于【计算机视觉】Lecture 18:广义的立体视觉:对极几何的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








