本文主要是介绍【math】大规模对称正定稀疏线性方程组的求解与代数多重网格,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大规模对称正定稀疏线性方程组的求解与代数多重网格
- 代数多重网格
- 问题定义
- 迭代法的优畧
- 几何多重网格
- 代数多重网格
代数多重网格
你好!代数多重网格一个很有意思的话题。
问题定义
很多问题都可以抽象为求解下列优化的问题:

对于图像问题,一方面由于绝大多数模型都只会建立某个像素与它局部之间的关系,因此线性方程组的系数矩阵 A A A通常满足某种特定的稀疏性;另一方面,由于图像分辨率较高,因此线性方程组维度实际上极大,导致快速计算难度较大。
因此,这个问题的****最终核心在于:如何快速求解一个稀疏大规模的对称正定的线性方程组。
迭代法的优畧
对于简单迭代法,如雅可比迭代,高斯-塞德尔迭代等,都存在高频快速收敛,低频难以收敛的问题。 简单来说,对于柏松问题:
在这里插入图片描述
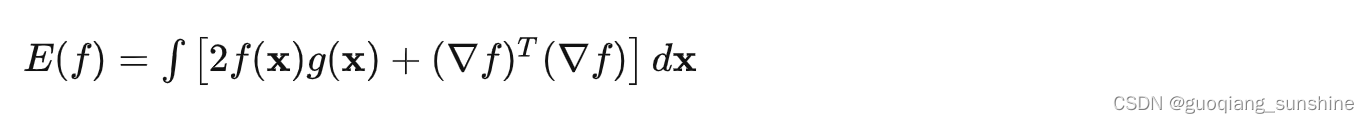

几何多重网格
为了解决低频收敛慢的问题,多重网格算法应运而生。 核心思想在于,在细网格上的低频可以变为粗网格上的高频。 注意到对于$ \lambda_{k}$ ,如果N变为N/2实际上可以认为频率变为了原来的两倍,那么收敛性自然会变好。 因此,我们可以先在细网格上迭代,消除了高频误差,然后放到粗网格迭代,消除细网格上的低频误差,然后再在粗网格上refine最终结果,大致流程如下图:
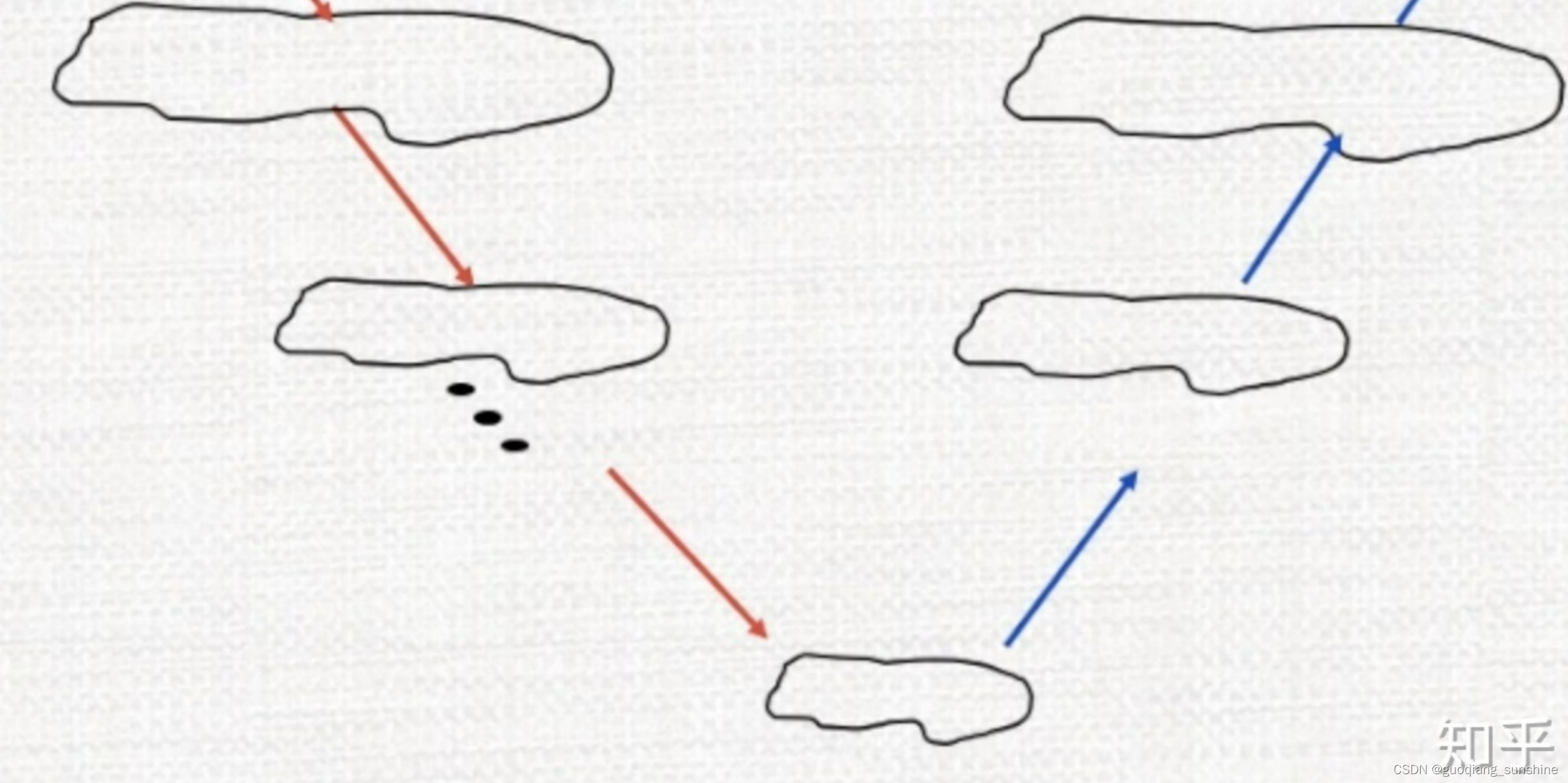
这个方法实际上是比较简单的,网格如下所示:
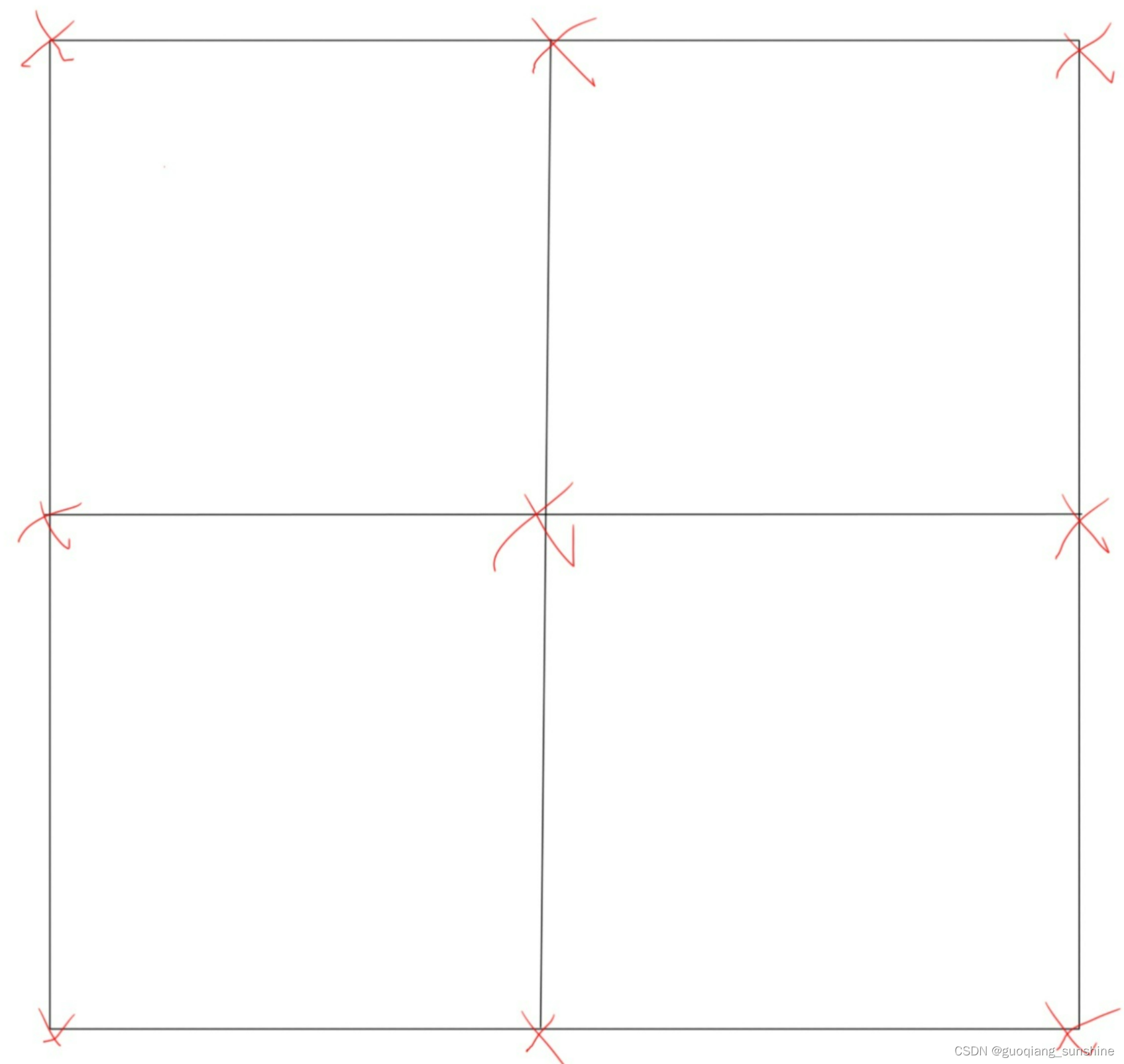
红色的点代表粗网格上的节点,如果我们将网格细化,那么,可以得到细网格的点:
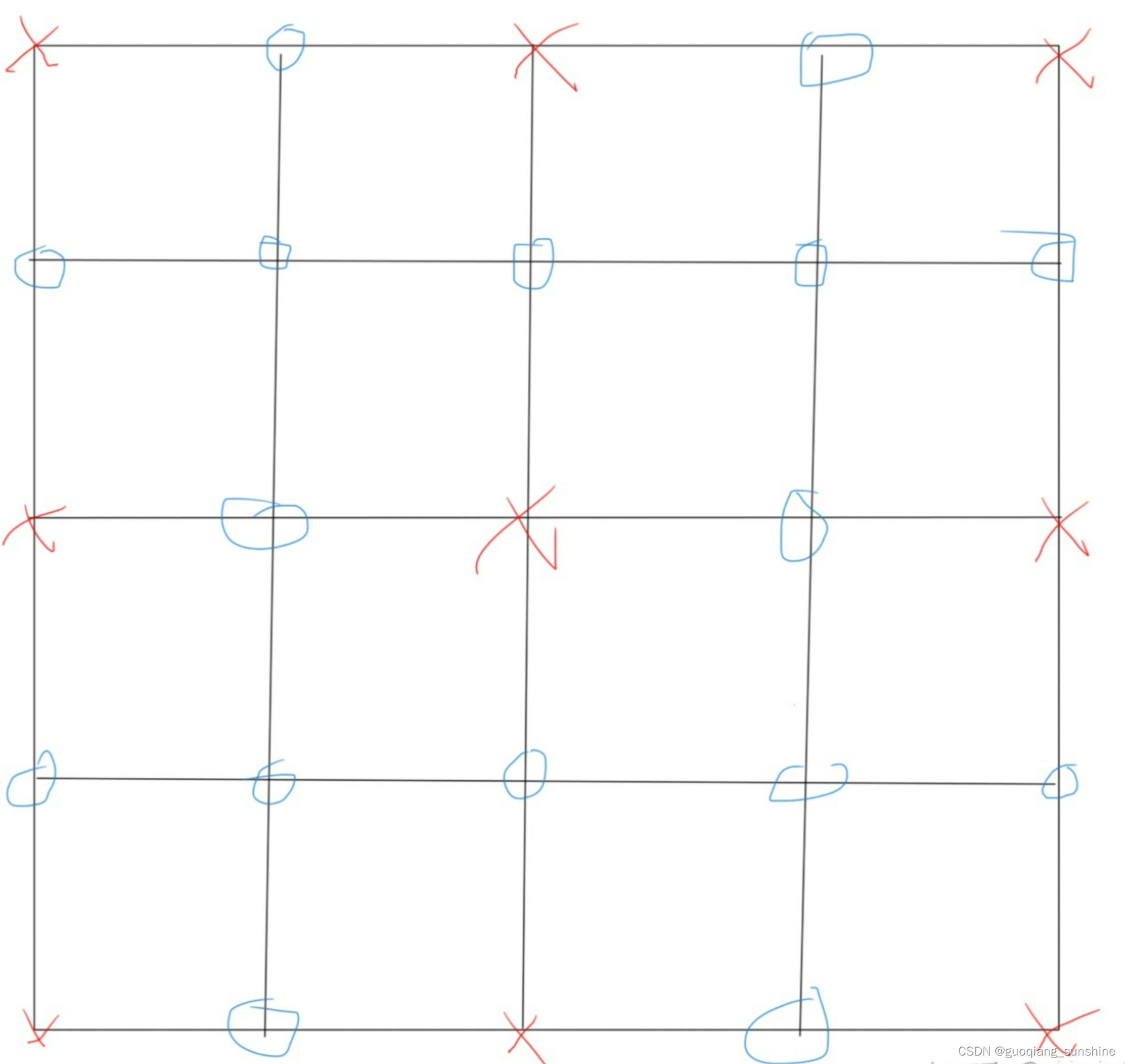
这些点的值通过粗网格插值而来,也就是说,几何多重网格实际上是依赖于实际的网格,人为设定了粗网格和细网格,从而设置的一种多重网格算法。
注意到这种方法细网格上的节点上一定有粗网格上的节点,因此原来如果粗细网格原来是同一个点,只需要将粗网格上的点赋值到细网格上,如果是新的点,那么需要对它进行插值,假设这个矩阵为 S , f k S,f_{k} S,fk 表示第k层网格上的节点,那么 f k = S ∗ f k − 1 f_{k} =S*f_{k-1} fk=S∗fk−1 ,因此我们只需要求解线性方程组:
A k − 1 f k − 1 = g k − 1 A_{k-1}f_{k-1}=g_{k-1} Ak−1fk−1=gk−1
之后插值即可。
但实际上这样做是不对的。回到最初的问题,我们要消除的是低频误差,也就是“光滑”误差, 在粗网格上迭代后的结果实际上和光滑没有太多关系,我们迭代后的结果,实际上是消除了高频的误差,也就是将误差变得光滑了。 因此,我们将误差传到粗网格上实际上是更为合理的,因此我们最终的迭代思路实际上是不断修正误差,即:
f k = f 0 + ∑ k = 1 M e k f_k=f_0 + \sum^{M}_{k=1}{e_k} fk=f0+k=1∑Mek
其中 e k e_k ek 代表每层网格给出的插值后的补偿误差。
那么,如何建立误差方程呢?
定义残差:
E k = A f k − b E_k =Af_k -b Ek=Afk−b
由此,我们有误差方程: A e k = E k Ae_k =E_k Aek=Ek
由于我们希望将低频误差放到粗网格上进行消除,因此我们实际上将 e k e_k ek “限制”到了粗网格上计算,然后再插值回粗网格上进行“误差补偿”。
最终,我们实际上计算了:
K k − 1 e k − 1 ′ = E k − 1 K_{k-1} e^{'}_{k-1} = E_{k-1} Kk−1ek−1′=Ek−1
然后插值得到 e k − 1 = S ∗ e k − 1 ′ e_{k-1}=S*e^{'}_{k-1} ek−1=S∗ek−1′
最后补偿到 f 上。
代数多重网格
是否有一种方法可以依赖于系数矩阵本身的特性,从而设计一种多重网格方法,与实际网格无关,从而得到更好的收敛性呢?实际上是有的,这个方法就是代数多重网格。 由于我们现在没有了实际网格,那么实际上为了使用多重网格技术,我们需要回答两个问题:
- 要选择哪些节点为粗网格上的节点
- 如何插值
对于问题1,实际上我们是需要准从两个原则:得到的粗网格节点能够通过插值表示细网格节点,或者说粗网格节点一定原来有和细网格节点相连。另一方面,我们希望粗节点能够尽量少,从而求解线性方程组的规模可以更小。 对于这个问题有个经典方法: 即Ruge提出来的方法
对于问题2,回答了两个子问题:
- 插值公式长什么样
2)粗网格上的线性方程组长什么样
通常如果插值矩阵为 S k S_k Sk ,那么粗网格上的线性方程组的系数矩阵构建为:KaTeX parse error: Expected group after '_' at position 2: S_̲^{T}_k A_kS_k
因此实际上核心还是在于如何插值。
假设 a i j a_{ij} aij表示连接i和j节点的边的权重,同时我们认为残差几乎为0,由此可以得到:
r i = a i i e i + ∑ a i j e j ≈ 0 r_i = a_{ii}e_i + \sum{a_{ij}e_j} \approx 0 ri=aiiei+∑aijej≈0
由此:
a i i e i ≈ − ∑ a i j e j a_{ii}e_i \approx- \sum{a_{ij}e_j} aiiei≈−∑aijej
由于这些边连接的节点可以分为3类:
细网格上的节点 e f e_f ef
粗网格上的节点 e c e_c ec
连接极弱的节点 e w e_w ew
若用C表示粗节点误差集合,F表示细节点误差集合,W表示弱连接集合,可以将求和部分分为三块:
a i i e i ≈ − ∑ j ∈ C a i j e j − ∑ j ∈ F a i j e j a_{ii}e_i \approx- \sum_{j \in C}{a_{ij}e_j} - \sum_{j \in F}{a_{ij}e_j} aiiei≈−j∈C∑aijej−j∈F∑aijej
由于弱连接集合的连接已经足够弱,因此我们强制认为这部分的 e j = e i e_j=e_i ej=ei ,由此可以得到新的近似公式:
( a i i + ∑ j ∈ W a i j ) e i ≈ − ∑ j ∈ C a i j e j − ∑ j ∈ F a i j e j (a_{ii} + \sum_{j \in W}{a_{ij}})e_i \approx- \sum_{j \in C}{a_{ij}e_j} - \sum_{j \in F}{a_{ij}e_j} (aii+j∈W∑aij)ei≈−j∈C∑aijej−j∈F∑aijej
对于粗网格上的 e j e_j ej实际上在粗网格上已经算出,而细网格上的 e j e_j ej 实际上是没有的。 对于这部分有连接的细网格上的 e j e_j ej ,我们找到和它相连的所有粗网格的节点 e j c e_{jc} ejc ,通过公式:
e j = ∑ a j , j c e j c ∑ a j , j c e_j = \frac{ \sum{a_{j,jc}e_{jc}}}{ \sum{a_{j,jc}}} ej=∑aj,jc∑aj,jcejc
对它进行近似计算。
这篇关于【math】大规模对称正定稀疏线性方程组的求解与代数多重网格的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




