学习笔记：斯坦福2017季CS231n深度视觉识别课程视频（by Fei-Fei Li, Justin Johnson, Serena Yeung）最优化笔记

最优化（上）

简介

对于图像数据x_i，如果基于参数集W做出的分类预测与真实情况比较一致，那么计算出来的损失值L就很低。现在介绍第三个，也是最后一个关键部分：最优化Optimization。最优化是寻找能使得损失函数值最小化的参数W的过程。

损失函数可视化

最优化

策略#1：随机搜索

核心思路：迭代优化。当然，我们肯定能做得更好些。核心思路是：虽然找到最优的权重W非常困难，甚至是不可能的（尤其当W中存的是整个神经网络的权重的时候），但如果问题转化为：对一个权重矩阵集W取优，使其损失值稍微减少。那么问题的难度就大大降低了。换句话说，我们的方法从一个随机的W开始，然后对其迭代取优，每次都让它的损失值变得更小一点。

我们的策略是从随机权重开始，然后迭代取优，从而获得更低的损失值。

蒙眼徒步者的比喻：一个助于理解的比喻是把你自己想象成一个蒙着眼睛的徒步者，正走在山地地形上，目标是要慢慢走到山底。在CIFAR-10的例子中，这山是30730维的（因为W是3073x10）。我们在山上踩的每一点都对应一个的损失值，该损失值可以看做该点的海拔高度。

策略#2：随机局部搜索

第一个策略可以看做是每走一步都尝试几个随机方向，如果某个方向是向山下的，就向该方向走一步。这次我们从一个随机W开始，然后生成一个随机的扰动dW ，只有当[公式]的损失值变低，我们才会更新。这个过程的具体代码如下：

W = np.random.randn(10, 3073) * 0.001 # 生成随机初始W
bestloss = float("inf")
for i in xrange(1000):step_size = 0.0001Wtry = W + np.random.randn(10, 3073) * step_size # 有随机扰动loss = L(Xtr_cols, Ytr, Wtry)if loss < bestloss:W = Wtrybestloss = lossprint 'iter %d loss is %f' % (i, bestloss)

使用同样的数据（1000），这个方法可以得到21.4%的分类准确率。这个比策略一好，但是依然过于浪费计算资源。

策略#3：跟随梯度

前两个策略中，我们是尝试在权重空间中找到一个方向，沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向，因为可以直接计算出最好的方向，==这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度（gradient）。==在蒙眼徒步者的比喻中，这个方法就好比是感受我们脚下山体的倾斜程度，然后向着最陡峭的下降方向下山。

在一维函数中，斜率是函数在某一点的瞬时变化率。梯度是函数的斜率的一般化表达，它不是一个值，而是一个向量。在输入空间中，梯度是各个维度的斜率组成的向量（或者称为导数derivatives）。（这是我理解梯度最深的一次 。对一维函数的求导公式如下：

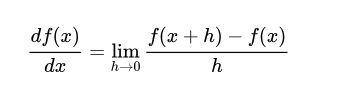
当函数有多个参数的时候，我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量。

最优化（下）

梯度计算

计算梯度有两种方法：一个是缓慢的近似方法（数值梯度法），但实现相对简单。另一个方法（分析梯度法）计算迅速，结果精确，但是实现时容易出错，且需要使用微分。现在对两种方法进行介绍：

使用有限差值进行数值计算

上节中的公式已经给出数值计算梯度的方法。下面代码是一个输入为函数f和向量x，计算f的梯度的通用函数，它返回函数f在点x处的梯度：

def eval_numerical_gradient(f, x):"""  一个f在x处的数值梯度法的简单实现- f是只有一个参数的函数- x是计算梯度的点""" fx = f(x) # 在原点计算函数值grad = np.zeros(x.shape)h = 0.00001# 对x中所有的索引进行迭代it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])while not it.finished:# 计算x+h处的函数值ix = it.multi_indexold_value = x[ix]x[ix] = old_value + h # 增加hfxh = f(x) # 计算f(x + h)x[ix] = old_value # 存到前一个值中 (非常重要)# 计算偏导数grad[ix] = (fxh - fx) / h # 坡度it.iternext() # 到下个维度return grad

根据上面的梯度公式，代码对所有维度进行迭代，在每个维度上产生一个很小的变化h，通过观察函数值变化，计算函数在该维度上的偏导数。最后，所有的梯度存储在变量grad中。

在梯度负方向上更新：在上面的代码中，为了计算W_new，要注意我们是向着梯度df的负方向去更新，这是因为我们希望损失函数值是降低而不是升高。

步长的影响
效率的问题

微分计算梯度

使用有限差值近似计算梯度比较简单，但缺点在于终究只是近似（因为我们对于h值是选取了一个很小的数值，但真正的梯度定义中h趋向0的极限），且耗费计算资源太多。

第二个梯度计算方法是利用微分来分析，能得到计算梯度的公式（不是近似），用公式计算梯度速度很快，唯一不好的就是实现的时候容易出错。为了解决这个问题，在实际操作时常常将分析梯度法的结果和数值梯度法的结果作比较，以此来检查其实现的正确性，这个步骤叫做梯度检查。

梯度下降

现在可以计算损失函数的梯度了，程序重复地计算梯度然后对参数进行更新，这一过程称为梯度下降，他的普通版本是这样的：

# 普通的梯度下降
while True:weights_grad = evaluate_gradient(loss_fun, data, weights)weights += - step_size * weights_grad # 进行梯度更新
在这里插入代码片

这个简单的循环在所有的神经网络核心库中都有。虽然也有其他实现最优化的方法（比如LBFGS），但是到目前为止，梯度下降是对神经网络的损失函数最优化中最常用的方法。

课程中，我们会在它的循环细节增加一些新的东西（比如更新的具体公式），但是核心思想不变，那就是我们一直跟着梯度走，直到结果不再变化。

小节

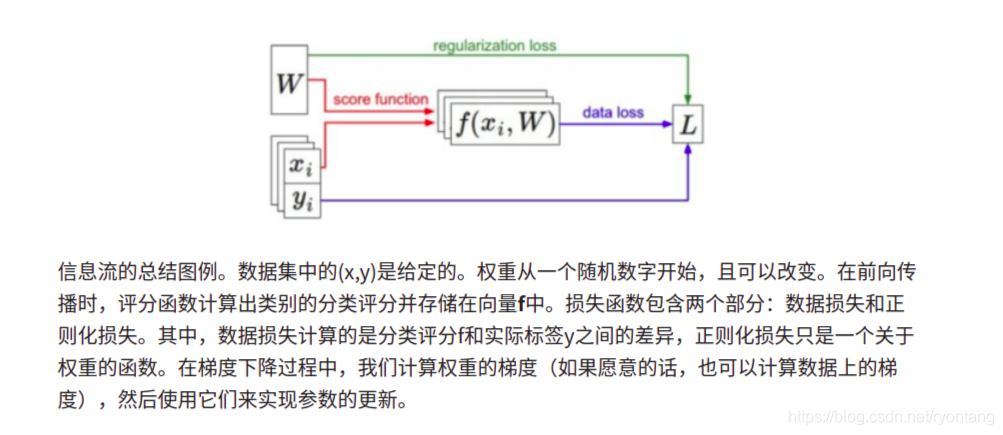
参考来源：
https://zhuanlan.zhihu.com/p/21360434?refer=intelligentunit