johnson专题

所有节点最短路径的Johnson实现

一、数据集形式其中：6105（节点个数） 7035（边数） 0（id） 1609（起始边） 1622（终边） 57.403187（权重）二、数据集数据集下载链接三、实现代码 // Dijkstra.cpp : Defines the entry point for the console application.//#include "stdafx.h"#include

图论 —— 最短路 —— Johnson 算法

【概述】对于单源最短路来说，有时间复杂度为 O(E+VlogV) 要求权值非负的 Dijkstra，时间复杂度为 O(VE) 适用于带负权值的 Bellman Ford 对于全源最短路来说，除了时间复杂度为 O(V*V*V) 利用动态规划思想的 Floyd 算法外，可以认为是单源最短路径的推广，即分别以每个顶点为源点求其至其他顶点的最短距离对于每个顶点利用 Ford 算法，时间复杂度为

Johnson算法实现原理和优化策略

Johnson算法是一种用于在加权图中找到所有顶点对之间最短路径的算法。它结合了Dijkstra算法和Bellman-Ford算法的优点，可以处理负权边，但不适用于负权环。本文将详细介绍Johnson算法的实现原理、优化策略，以及如何应用该算法。 1. Johnson算法概述 1.1 算法步骤 Johnson算法分为三个主要步骤：边的重标定（Reweighting）：给图中的每一条边赋

Rod Johnson平衡的质疑：Spring维护策略的再次调整

不管你承不承认，Spring实际上已经是实事上JAVA企业开发的标准，SpringSource最近策略维护策略变更已经在JAVA世界满城风雨。 Rod终于忍不住在他的BLOG就SpringSource最近策略维护策略变更一事再次进行了新的调整，以求开源与商业达到平衡。Rod希望就此机会一扫大家的顾虑与疑问，表明 SpringSource坚持永远拥护开源的决心。原文请看： http:/

稀疏图带负边的全源最短路Johnson算法

BellmanFord算法 Johnson算法解决的问题带负权的稀疏图的全源最短路算法流程重新设置的每条边的权重都大于或等于0，跑完Djikstra后得到的全源最短路，记得要还原，即：f(u,v) = d(u,v) - h[u] + h[v] 例题

Yeo-Johnson变换在R语言中的应用

R语言中应用Yeo-Johnson变换。我们将首先生成一组示例数据，这组数据将故意包含一些非正值，以展示Yeo-Johnson变换处理这类数据的能力。示例数据生成我们将生成一组含有正值、零值和负值的数据。使用forecast包应用Yeo-Johnson变换 # 安装和加载forecast包if (!requireNamespace("forecast", quietly = TRU

Luogu P5905 【模板】全源最短路（Johnson）题解全源最短路 Johnson算法

题目链接：Luogu P5905 【模板】全源最短路（Johnson）题目描述：给定一张有向图，求出任意两点之间的最短路。题解：使用Johnson算法即可。其思想就是将一个含有负权边的图变成无负权边的图之后，跑n次Dijkstra算法。对于一个没有负环的图，具体地：建立超级源点，使其到每个结点建立一条权重为0的有向边，通过Bellman-Ford以超级源点为起点计算一次单元

Johnson算法寻找图中的所有简单环路

Johnson算法论文：https://www.cs.tufts.edu/comp/150GA/homeworks/hw1/Johnson%2075.PDF Johnson算法讲解视频：https://www.youtube.com/watch?v=johyrWospv0 一篇解释原理较好的博客：https://blog.csdn.net/Azeroit/article/details/105

信号完整性视频教程Douglas Brooks Howard Johnson

信号完整性领域两个大牛的视频教程 1.道格拉斯布鲁克斯（Douglas Brooks），UltraCAD公司的总裁，著有图书《Signal Integrity Issues and Printed Circuit Board Design》、《PCB Currents: How They Flow, How They React 》视频教程 PCB Signal Integrity LiveL

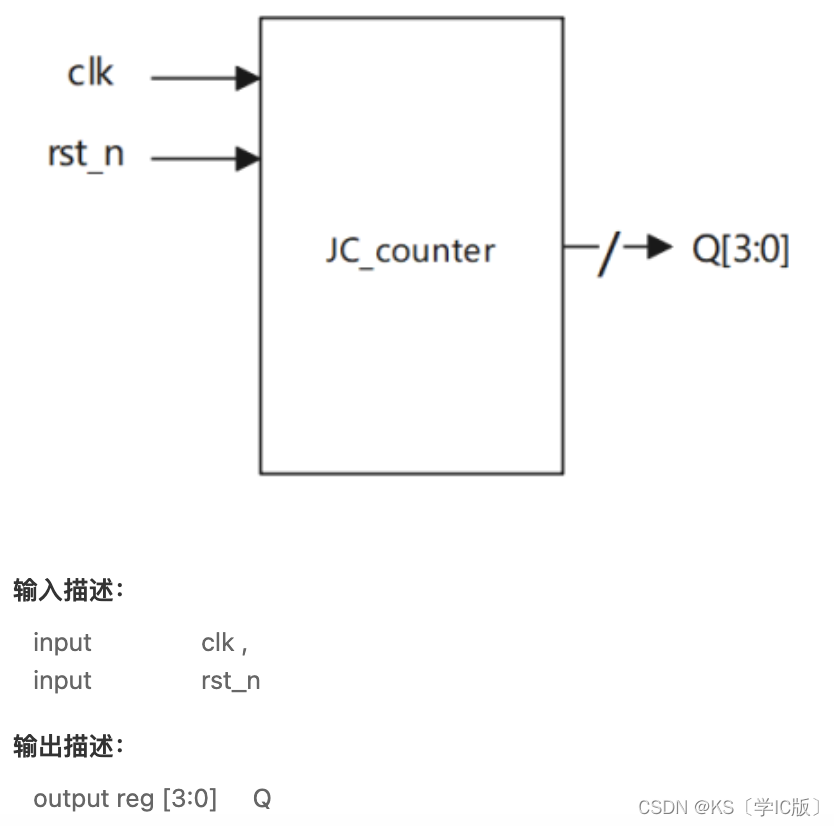
「Verilog学习笔记」 Johnson Counter

专栏前言本专栏的内容主要是记录本人学习Verilog过程中的一些知识点，刷题网站用的是牛客网 `timescale 1ns/1nsmodule JC_counter(input clk ,input rst_n,output reg [3:0] Q );always @ (posedge clk or neg

学习笔记：斯坦福2017季CS231n深度视觉识别课程视频（by Fei-Fei Li, Justin Johnson, Serena Yeung）图像分类笔记

CS231n课程笔记翻译：图像分类笔记（上）图像分类、数据驱动方法和流程目标：这一节我们将介绍图像分类问题。所谓图像分类问题，就是已有固定的分类标签集合，然后对于输入的图像，从分类标签集合中找出一个分类标签，最后把分类标签分配给该输入图像在后面的课程中，我们可以看到计算机视觉领域中很多看似不同的问题（比如物体检测和分割），都可以被归结为图像分类问题例子：以下图为例，图像分类模型读取该

学习笔记：斯坦福2017季CS231n深度视觉识别课程视频（by Fei-Fei Li, Justin Johnson, Serena Yeung）线性分类笔记

线性分类笔记（上）线性分类器简介上一篇笔记介绍了图像分类问题。图像分类的任务，就是从已有的固定分类标签集合中选择一个并分配给一张图像。我们还介绍了k-Nearest Neighbor （k-NN）分类器，该分类器的基本思想是通过将测试图像与训练集带标签的图像进行比较，来给测试图像打上分类标签。k-Nearest Neighbor分类器存在以下不足：分类器必须记住所有训练数据并将其存储起

学习笔记：斯坦福2017季CS231n深度视觉识别课程视频（by Fei-Fei Li, Justin Johnson, Serena Yeung）反向传播笔记

简介目标：本节将帮助读者对反向传播形成直观而专业的理解。反向传播是利用链式法则递归计算表达式的梯度的方法。理解反向传播过程及其精妙之处，对于理解、实现、设计和调试神经网络非常关键。简单表达式和理解梯度复合表达式，链式法则，反向传播直观理解反向传播反向传播是一个优美的局部过程。在整个计算线路图中，每个门单元都会得到一些输入并立即计算两个东西： 1. 这个门的输出值，和

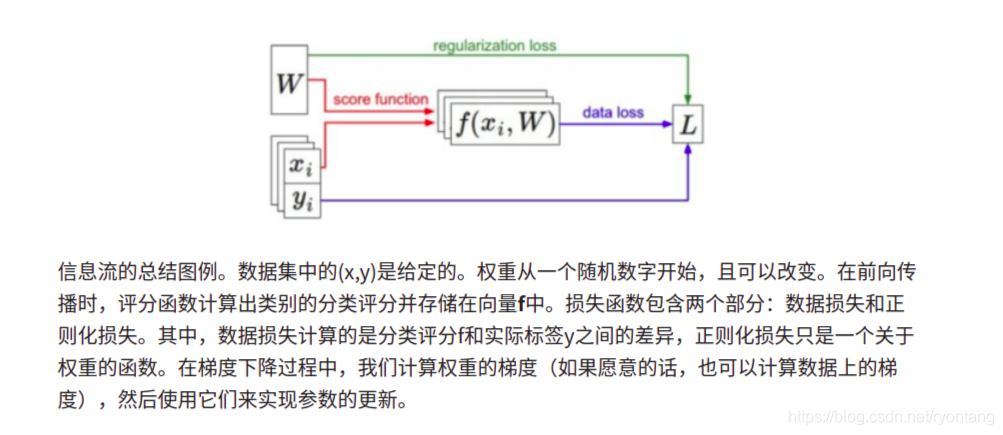
学习笔记：斯坦福2017季CS231n深度视觉识别课程视频（by Fei-Fei Li, Justin Johnson, Serena Yeung）最优化笔记

最优化（上）简介对于图像数据xi，如果基于参数集W做出的分类预测与真实情况比较一致，那么计算出来的损失值L就很低。现在介绍第三个，也是最后一个关键部分：最优化Optimization。最优化是寻找能使得损失函数值最小化的参数W的过程。损失函数可视化最优化策略#1：随机搜索核心思路：迭代优化。当然，我们肯定能做得更好些。核心思路是：虽然找到最优的权重W非常困难，甚至是不可能的