用于物体识别和跟踪的下游任务自监督学习-2-（计算机视觉中的距离度量+损失函数）

本文主要是介绍用于物体识别和跟踪的下游任务自监督学习-2-（计算机视觉中的距离度量+损失函数），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2.4 计算机视觉中的距离度量

在深度学习和计算机视觉中，距离度量通常用于比较图像、视频或其他数据的特征或嵌入。根据具体任务和数据属性，可以使用不同类型的距离度量。下面介绍了深度学习和计算机视觉中使用的一些常见类型的距离度量。

余弦相似性距离：余弦相似性测量向量空间模型（VSM）中两个向量之间的距离。余弦相似性Sc（τa，τp）和两个向量τa和τp之间对应的余弦距离Dc（τa、τp）可以定义如下2.6式子

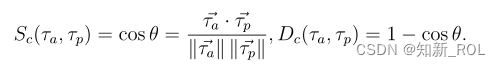
软余弦相似距离是自然语言处理中提出的传统余弦距离[61]的修改版本，它考虑了余弦距离中两个特征向量之间的相似性。

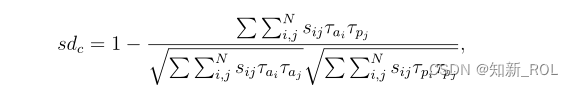
如果τai和τpj之间没有相似性，则对于i 6=j和sii=1，sij=0，这减少到传统的余弦相似距离Dc（等式2.6）

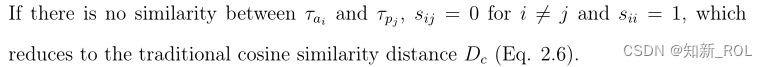
Mahalanobis距离：Mahalano比斯距离测量点和分布之间的距离。与欧几里得距离不同Mahalanobis 30距离考虑了变量之间的相关性。在这个度量中，每个变量根据其相关性对距离做出贡献。x∈Rp和p变量分布fx（.）的平均值µ=E（x）之间的马氏距离D（x，µ）可以定义为

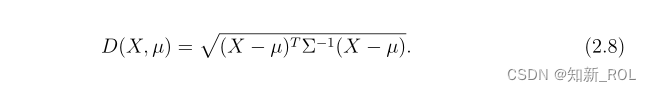
对于单位协方差矩阵，Mahalanobis距离变为欧几里得距离。

豪斯多夫距离（Hausdorff Distance）：豪斯多夫距离度量测量两组点之间的相似性，并定义为一组点中任意点与另一组点之间最接近点之间的最高距离。两组点τa和τp之间的有向豪斯多夫距离[62]可以定义为每个点x∈τa与其最近邻居y∈τp

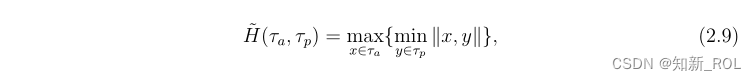
其中||*||是欧几里得距离函数。由于~H（τa，τp）6=~H（σp，τa），豪斯多夫距离也被定义为两个方向上有向豪斯多夫距离的最大值，即。

Frechet距离：Fréchet距离[63,64]测量两条曲线之间的相似性。它被定义为两条曲线上对应点之间的最大距离在两条曲线的所有可能对齐上的最小值。

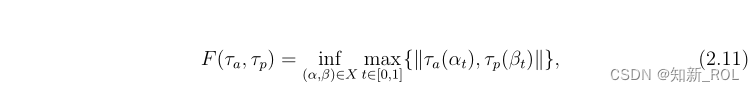
其中，两条2D多边形曲线τa和τp之间的Fréchet距离F（τa，τp）是τa（αt）和τp（βt）之间所有欧几里得距离的最大值的所有α，β的下确界（最大下界）。这里，t∈[0,1]表示当我们计算两个曲线点之间的距离时的时间实例。为了解决O（n2-log（n2））的计算复杂度，在[65]中提出了离散Frèchet距离，其计算复杂度为O（n2）。离散Frèchet距离经常被用作图像配准、对象识别和计算几何中的相似性度量。