计算几何(基础知识凸包半平面交最小圆覆盖三维计算几何基础 三维凸包 旋转卡壳三角剖分扫描线自适应辛普森积分

2023-10-13 09:20
文章标签 基础 计算 覆盖 最小 旋转 三维 基础知识 几何 积分 适应 剖分 平面 扫描线 三角 凸包 包半 辛普森 卡壳

本文主要是介绍计算几何(基础知识凸包半平面交最小圆覆盖三维计算几何基础 三维凸包 旋转卡壳三角剖分扫描线自适应辛普森积分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第四章 计算几何

基础知识

  1. 前置知识点
    (1) pi = acos(-1);
    (2) 余弦定理 c^2 = a^2 + b^2 - 2abcos(t)

  2. 浮点数的比较
    const double eps = 1e-8;
    int sign(double x) // 符号函数
    {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
    }
    int cmp(double x, double y) // 比较函数
    {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
    }

  3. 向量
    3.1 向量的加减法和数乘运算
    3.2 内积（点积） A·B = |A||B|cos©
    (1) 几何意义：向量A在向量B上的投影与B的长度的乘积。
    (2) 代码实现
    double dot(Point a, Point b)
    {
    return a.x * b.x + a.y * b.y;
    }
    3.3 外积（叉积） AxB = |A||B|sin©
    (1) 几何意义：向量A与B张成的平行四边形的有向面积。B在A的逆时针方向为正。
    (2) 代码实现
    double cross(Point a, Point b)
    {
    return a.x * b.y - b.x * a.y;
    }
    3.4 常用函数
    3.4.1 取模
    double get_length(Point a)
    {
    return sqrt(dot(a, a));
    }
    3.4.2 计算向量夹角
    double get_angle(Point a, Point b)
    {
    return acos(dot(a, b) / get_length(a) / get_length(b));
    }
    3.4.3 计算两个向量构成的平行四边形有向面积
    double area(Point a, Point b, Point c)
    {
    return cross(b - a, c - a);
    }
    3.4.5 向量A顺时针旋转C的角度：
    Point rotate(Point a, double angle)
    {
    return Point(a.x * cos(angle) + a.y * sin(angle), -a.x * sin(angle) + a.y * cos(angle));
    }

  4. 点与线
    4.1 直线定理
    (1) 一般式 ax + by + c = 0
    (2) 点向式 p0 + vt
    (3) 斜截式 y = kx + b
    4.2 常用操作
    (1) 判断点在直线上 A x B = 0
    (2) 两直线相交
    // cross(v, w) == 0则两直线平行或者重合
    Point get_line_intersection(Point p, Vector v, Point q, vector w)
    {
    vector u = p - q;
    double t = cross(w, u) / cross(v, w);
    return p + v * t;
    }
    (3) 点到直线的距离
    double distance_to_line(Point p, Point a, Point b)
    {
    vector v1 = b - a, v2 = p - a;
    return fabs(cross(v1, v2) / get_length(v1));
    }
    (4) 点到线段的距离
    double distance_to_segment(Point p, Point a, Point b)
    {
    if (a == b) return get_length(p - a);
    Vector v1 = b - a, v2 = p - a, v3 = p - b;
    if (sign(dot(v1, v2)) < 0) return get_length(v2);
    if (sign(dot(v1, v3)) > 0) return get_length(v3);
    return distance_to_line(p, a, b);
    }
    (5) 点在直线上的投影
    double get_line_projection(Point p, Point a, Point b)
    {
    Vector v = b - a;
    return a + v * (dot(v, p - a) / dot(v, v));
    }
    (6) 点是否在线段上
    bool on_segment(Point p, Point a, Point b)
    {
    return sign(cross(p - a, p - b)) == 0 && sign(dot(p - a, p - b)) <= 0;
    }
    (7) 判断两线段是否相交
    bool segment_intersection(Point a1, Point a2, Point b1, Point b2)
    {
    double c1 = cross(a2 - a1, b1 - a1), c2 = cross(a2 - a1, b2 - a1);
    double c3 = cross(b2 - b1, a2 - b1), c4 = cross(b2 - b1, a1 - b1);
    return sign(c1) * sign(c2) <= 0 && sign(c3) * sign(c4) <= 0;
    }

  5. 多边形
    5.1 三角形
    5.1.1 面积
    (1) 叉积
    (2) 海伦公式
    p = (a + b + c) / 2;
    S = sqrt(p(p - a) * (p - b) * (p - c));
    5.1.2 三角形四心
    (1) 外心，外接圆圆心
    三边中垂线交点。到三角形三个顶点的距离相等
    (2) 内心，内切圆圆心
    角平分线交点，到三边距离相等
    (3) 垂心
    三条垂线交点
    (4) 重心
    三条中线交点（到三角形三顶点距离的平方和最小的点，三角形内到三边距离之积最大的点）
    5.2 普通多边形
    通常按逆时针存储所有点
    5.2.1 定义
    (1) 多边形
    由在同一平面且不再同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形
    (2) 简单多边形
    简单多边形是除相邻边外其它边不相交的多边形
    (3) 凸多边形
    过多边形的任意一边做一条直线，如果其他各个顶点都在这条直线的同侧，则把这个多边形叫做凸多边形
    任意凸多边形外角和均为360°
    任意凸多边形内角和为(n−2)180°
    5.2.2 常用函数
    (1) 求多边形面积（不一定是凸多边形）
    我们可以从第一个顶点除法把凸多边形分成n − 2个三角形，然后把面积加起来。
    double polygon_area(Point p[], int n)
    {
    double s = 0;
    for (int i = 1; i + 1 < n; i ++ )
    s += cross(p[i] - p[0], p[i + 1] - p[i]);
    return s / 2;
    }
    (2) 判断点是否在多边形内（不一定是凸多边形）
    a. 射线法，从该点任意做一条和所有边都不平行的射线。交点个数为偶数，则在多边形外，为奇数，则在多边形内。
    b. 转角法
    (3) 判断点是否在凸多边形内
    只需判断点是否在所有边的左边（逆时针存储多边形）。
    5.3 皮克定理
    皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式该公式可以表示为:
    S = a + b/2 - 1
    其中a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积。

  6. 圆
    (1) 圆与直线交点
    (2) 两圆交点
    (3) 点到圆的切线
    (4) 两圆公切线
    (5) 两圆相交面积

2983. 玩具

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef pair<int, int> PII;
#define x first
#define y second
//#define d lld
int n;
PII a[5050],b[5050];//a在下面，b在上面
int ans[5050];
int cross(int x1,int y1,int x2,int y2){return x1*y2-x2*y1;
}
int area(PII a,PII b,PII c){return cross(b.x-a.x,b.y-a.y , c.x-a.x,c.y-a.y);
}
int find(int x,int y){int l=0,r=n;while(l<r){int mid=l+r>>1;if(area(a[mid],b[mid],{x,y})>0)r=mid;else l=mid+1;}return r;
}
signed main(){bool is_first=1;while(scanf("%lld",&n),n){int m,x1,y1,x2,y2;scanf("%lld%lld%lld%lld%lld",&m,&x1,&y1,&x2,&y2);//左上角，右下角for(int i=0;i<n;i++){int u,l;cin>>u>>l;b[i]={u,y1};//右上角a[i]={l,y2};//左下角}a[n]={x2,y2};b[n]={x2,y1};memset(ans,0,sizeof ans);while(m--){int x,y;cin>>x>>y;ans[find(x,y)]++;}if(is_first)is_first=0;else puts("");for(int i=0;i<=n;i++)printf("%lld: %lld\n",i,ans[i]);}
}

2984. 线段

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
typedef pair<double, double> PDD;
#define x first
#define y second
int T,n,m;
const int N = 220;
const double eps = 1e-8;
PDD q[N],a[N],b[N];
bool cmp(double x,double y){if(fabs(x-y)<eps)return 0;if(x<y)return -1;else return 1;
}
int sign(double t){if(fabs(t)<eps)return 0;if(t>0)return 1;else return -1;
}
double cross(double x1,double y1,double x2,double y2){return x1*y2-x2*y1;
}
double area(PDD a,PDD b,PDD c){return cross(b.x-a.x,b.y-a.y,c.x-a.x,c.y-a.y);
}
bool check(){for(int i=0;i<n*2;i++){for(int j=i+1;j<n*2;j++){if( !cmp(q[i].x,q[j].x) && !cmp(q[i].y,q[j].y) )continue;bool ok=1;for(int k=0;k<n;k++){int zuo=sign(area(q[j],q[i],a[k]));int you=sign(area(q[j],q[i],b[k]));if(zuo*you>0){ok=false;break;}}if(ok)return 1;}}return 0;
}signed main(){cin>>T;while(T--){scanf("%d",&n);for(int i=0,k=0;i<n;i++){double x1,y1,x2,y2;scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);q[k++]={x1,y1},q[k++]={x2,y2};a[i]  ={x1,y1},b[i]  ={x2,y2};}if(check())puts("Yes!");else puts("No!");}
}

凸包

Andrew算法
时间复杂度O(nlogn)【时间主要是在对坐标的快排上】

Andrew算法：Andrew算法是对Graham扫描法的改进。-

原理：

利用夹角，让整个图形保持左转。先将最左边的前两个点加入栈中，每次加入新点时判断是否左拐（叉积大于0），如果是就将新点直接加入；如果不是，就弹出栈顶，直到左拐，将新点加入栈中。【注意，栈中要保证至少有一个元素，也就是top>=2的时候才可以弹出栈顶】第一遍找的都是y小的点，也就是下凸包，上面没有，然后我们反着再来一遍。

流程：

1.将所有点进行快排，以x为第一关键字，y为第二关键字升序排序

2.先从左至右维护凸包的下半部分，然后再从右至左谓语上半部分。

3.将第一个点放入栈中，【这个点一定时凸包的最左边的点了，是不会清理掉的】，然后在将第二个点放入栈中。当栈中元素大于等于2的时候，就要判断栈顶元素是否还要保留。

如果新点在栈顶元素和次栈顶元素所组成的直线的右侧，那么，直接将新点加入栈中。

如果新点在栈顶元素和次栈顶元素所组成的直线的左侧，那么，将栈顶元素不断弹出，直到新点的位置出现在栈顶元素与次栈顶元素所在直线的右侧结束。

那么，我们这个过程，是从左往右走的，而且每次找的点都是在当前直线的右侧，也就是直线的下方向，那么我们得到的凸包就是我们的下半部分。

求上半部分的时候，从右往左排就自然而然是对的了。

1401. 围住奶牛

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 10010;int n;
PDD q[N];
int stk[N];
bool used[N];double get_dist(PDD a, PDD b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}PDD operator-(PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}double cross(PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double area(PDD a, PDD b, PDD c)
{return cross(b - a, c - a);
}double andrew()
{sort(q, q + n);int top = 0;for (int i = 0; i < n; i ++ ){while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0){// 凸包边界上的点即使被从栈中删掉，也不能删掉used上的标记if (area(q[stk[top - 1]], q[stk[top]], q[i]) < 0)used[stk[top -- ]] = false;else top -- ;}stk[ ++ top] = i;used[i] = true;}used[0] = false;for (int i = n - 1; i >= 0; i -- ){if (used[i]) continue;while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0)top -- ;stk[ ++ top] = i;}double res = 0;for (int i = 2; i <= top; i ++ )res += get_dist(q[stk[i - 1]], q[stk[i]]);return res;
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);double res = andrew();printf("%.2lf\n", res);return 0;
}

acwing和洛谷题目有点区别，acwing题目说了数据保证所有奶牛不会全部处在同一条直线上，洛谷题目没有，所以在洛谷上会wa，只要在判断边界的时候是一条直线也加入凸包，所以其实把判断上凸包和下凸包都不加等号就能过了，

2935. 信用卡凸包

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 40010;
const double pi = acos(-1);int n, cnt;
PDD q[N];
int stk[N], top;
bool used[N];PDD rotate(PDD a, double b)
{return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}double cross(PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double area(PDD a, PDD b, PDD c)
{return cross(b - a, c - a);
}double get_dist(PDD a, PDD b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}double andrew()
{sort(q, q + cnt);for (int i = 0; i < cnt; i ++ ){while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0){// 凸包边界上的点即使被从栈中删掉，也不能删掉used上的标记if (area(q[stk[top - 1]], q[stk[top]], q[i]) < 0)used[stk[top -- ]] = false;else top -- ;}stk[ ++ top] = i;used[i] = true;}used[0] = 0;for (int i = cnt - 1; i >= 0; i -- ){if (used[i]) continue;while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0)top -- ;stk[ ++ top] = i;}double res = 0;for (int i = 2; i <= top; i ++ )res += get_dist(q[stk[i - 1]], q[stk[i]]);return res;
}int main()
{scanf("%d", &n);double a, b, r;scanf("%lf%lf%lf", &a, &b, &r);a = a / 2 - r, b = b / 2 - r;int dx[] = {1, 1, -1, -1}, dy[] = {1, -1, -1, 1};while (n -- ){double x, y, z;scanf("%lf%lf%lf", &x, &y, &z);for (int i = 0; i < 4; i ++ ){auto t = rotate({dx[i] * b, dy[i] * a}, -z);q[cnt ++ ] = {x + t.x, y + t.y};}}double res = andrew();printf("%.2lf\n", res + 2 * pi * r);return 0;
}
```![在这里插入图片描述](https://img-blog.csdnimg.cn/94531295205b47189411fc1f81148c52.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA44GU44CA44KI44G244KT,size_20,color_FFFFFF,t_70,g_se,x_16)***************
## 半平面交
存储的是线，处理的也是线
如果给的是点，就先变成线
对于每两条直线，取左不取右
用一个双端队列while处理队尾然后处理队头
处理完毕后
先用队头更新队尾，再用队尾更新队头
然后把队头放进队尾
用ans数组存每两条线的交点----get_line_intersection（）函数
对得到的凸包求有向面积和
### 2803. 凸多边形
![在这里插入图片描述](https://img-blog.csdnimg.cn/3b8a63a418b640c59343be8b0a6782bb.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA44GU44CA44KI44G244KT,size_20,color_FFFFFF,t_70,g_se,x_16)
```cpp
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double,double> PDD;
const int N = 510;
const double eps = 1e-8;int cnt;
struct Line
{PDD st, ed;
}line[N];
PDD pg[N], ans[N];
int q[N];int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}double get_angle(const Line& a)
{return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);
}PDD operator-(PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}double cross(PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double area(PDD a, PDD b, PDD c)
{return cross(b - a, c - a);
}bool cmp(const Line& a, const Line& b)
{double A = get_angle(a), B = get_angle(b);if (!dcmp(A, B)) return area(a.st, a.ed, b.ed) < 0;return A < B;
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{auto u = p - q;double t = cross(w, u) / cross(v, w);return {p.x + v.x * t, p.y + v.y * t};
}PDD get_line_intersection(Line a, Line b)
{return get_line_intersection(a.st, a.ed - a.st, b.st, b.ed - b.st);
}// bc的交点是否在a的右侧
bool on_right(Line& a, Line& b, Line& c)
{auto o = get_line_intersection(b, c);return sign(area(a.st, a.ed, o)) <= 0;
}double half_plane_intersection()
{sort(line, line + cnt, cmp);int hh = 0, tt = -1;for (int i = 0; i < cnt; i ++ ){if (i && !dcmp(get_angle(line[i]), get_angle(line[i - 1]))) continue;while (hh + 1 <= tt && on_right(line[i], line[q[tt - 1]], line[q[tt]])) tt -- ;while (hh + 1 <= tt && on_right(line[i], line[q[hh]], line[q[hh + 1]])) hh ++ ;q[ ++ tt] = i;}while (hh + 1 <= tt && on_right(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt -- ;while (hh + 1 <= tt && on_right(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh ++ ;q[ ++ tt] = q[hh];int k = 0;for (int i = hh; i < tt; i ++ )ans[k ++ ] = get_line_intersection(line[q[i]], line[q[i + 1]]);double res = 0;for (int i = 1; i + 1 < k; i ++ )res += area(ans[0], ans[i], ans[i + 1]);return res / 2;
}int main()
{int n, m;scanf("%d", &n);while (n -- ){scanf("%d", &m);for (int i = 0; i < m; i ++ ) scanf("%lf%lf", &pg[i].x, &pg[i].y);//存点for (int i = 0; i < m; i ++ )line[cnt ++ ] = {pg[i], pg[(i + 1) % m]};//存线}double res = half_plane_intersection();printf("%.3lf\n", res);return 0;
}

2957. 赛车

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
#include <vector>#define x first
#define y secondusing namespace std;typedef long double LD;
typedef pair<int, int> PII;
typedef pair<LD, LD> PDD;
const int N = 10010;
const LD eps = 1e-18;int n, cnt;
struct Line
{PDD st, ed;vector<int> ids;
}line[N];
int ki[N], vi[N];
int q[N], ans[N];PDD operator-(PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}int sign(LD x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(LD x, LD y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}LD cross(PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}LD area(PDD a, PDD b, PDD c)
{return cross(b - a, c - a);
}LD get_angle(const Line& a)
{return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);
}bool cmp(const Line& a, const Line& b)
{LD A = get_angle(a), B = get_angle(b);if (!dcmp(A, B)) return area(a.st, a.ed, b.ed) < 0;return A < B;
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{auto u = p - q;LD t = cross(w, u) / cross(v, w);return {p.x + v.x * t, p.y + v.y * t};
}PDD get_line_intersection(Line& a, Line& b)
{return get_line_intersection(a.st, a.ed - a.st, b.st, b.ed - b.st);
}// 判断bc的交点是否在a的右侧
bool on_right(Line& a, Line& b, Line& c)
{auto o = get_line_intersection(b, c);return area(a.st, a.ed, o) < 0;
}void half_plane_intersection()
{sort(line, line + cnt, cmp);int hh = 0, tt = -1;for (int i = 0; i < cnt; i ++ ){if (i && !dcmp(get_angle(line[i - 1]), get_angle(line[i]))) continue;while (hh + 1 <= tt && on_right(line[i], line[q[tt - 1]], line[q[tt]])) tt -- ;while (hh + 1 <= tt && on_right(line[i], line[q[hh]], line[q[hh + 1]])) hh ++ ;q[ ++ tt] = i;}while (hh + 1 <= tt && on_right(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt -- ;while (hh + 1 <= tt && on_right(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh ++ ;int k = 0;for (int i = hh; i <= tt; i ++ )for (auto id: line[q[i]].ids)ans[k ++ ] = id;sort(ans, ans + k);printf("%d\n", k);for (int i = 0; i < k; i ++ ) printf("%d ", ans[i]);puts("");
}int main()
{map<PII, vector<int>> ids;scanf("%d", &n);for (int i = 1; i <= n; i ++ ) scanf("%d", &ki[i]);for (int i = 1; i <= n; i ++ ) scanf("%d", &vi[i]);for (int i = 1; i <= n; i ++ )ids[{ki[i], vi[i]}].push_back(i);line[cnt ++ ] = {{0, 10000}, {0, 0}};line[cnt ++ ] = {{0, 0}, {10000, 0}};for (auto& [k, v]: ids)line[cnt ++ ] = {{0, k.x}, {1, k.x + k.y}, v};half_plane_intersection();return 0;
}

最小圆覆盖

3028. 最小圆覆盖

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 100010;
const double eps = 1e-12;
const double PI = acos(-1);int n;
PDD q[N];
struct Circle
{PDD p;double r;
};int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}PDD operator+ (PDD a, PDD b)
{return {a.x + b.x, a.y + b.y};
}PDD operator* (PDD a, double t)
{return {a.x * t, a.y * t};
}PDD operator/ (PDD a, double t)
{return {a.x / t, a.y / t};
}double operator* (PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}PDD rotate(PDD a, double b)
{return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}double get_dist(PDD a, PDD b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{auto u = p - q;double t = w * u / (v * w);return p + v * t;
}pair<PDD, PDD> get_line(PDD a, PDD b)
{//求垂直ab的向量，就是ab的垂直平分线然后返回中点和顺时针旋转90°的向量return {(a + b) / 2, rotate(b - a, PI / 2)};
}Circle get_circle(PDD a, PDD b, PDD c)
{auto u = get_line(a, b), v = get_line(a, c);auto p = get_line_intersection(u.x, u.y, v.x, v.y);return {p, get_dist(p, a)};
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);random_shuffle(q, q + n);Circle c({q[0], 0});for (int i = 1; i < n; i ++ )if (dcmp(c.r, get_dist(c.p, q[i])) < 0){c = {q[i], 0};for (int j = 0; j < i; j ++ )if (dcmp(c.r, get_dist(c.p, q[j])) < 0){c = {(q[i] + q[j]) / 2, get_dist(q[i], q[j]) / 2};for (int k = 0; k < j; k ++ )if (dcmp(c.r, get_dist(c.p, q[k])) < 0)c = get_circle(q[i], q[j], q[k]);}}printf("%.10lf\n", c.r);printf("%.10lf %.10lf\n", c.p.x, c.p.y);return 0;
}

2785. 信号增幅仪

这其实求的是一个最小椭圆覆盖
但本质上还是最小圆覆盖
只需要一些仿射变换就好了
在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 50010;
const double eps = 1e-12;
const double PI = acos(-1);int n;
PDD q[N];
struct Circle
{PDD p;double r;
};int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}PDD operator+ (PDD a, PDD b)
{return {a.x + b.x, a.y + b.y};
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}PDD operator* (PDD a, double t)
{return {a.x * t, a.y * t};
}PDD operator/ (PDD a, double t)
{return {a.x / t, a.y / t};
}double operator* (PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}PDD rotate(PDD a, double b)
{return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}double get_dist(PDD a, PDD b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{auto u = p - q;double t = w * u / (v * w);return p + v * t;
}pair<PDD, PDD> get_line(PDD a, PDD b)
{return {(a + b) / 2, rotate(b - a, PI / 2)};
}Circle get_circle(PDD a, PDD b, PDD c)
{auto u = get_line(a, b), v = get_line(a, c);auto p = get_line_intersection(u.x, u.y, v.x, v.y);return {p, get_dist(p, a)};
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);double a, p;scanf("%lf%lf", &a, &p);for (int i = 0; i < n; i ++ ){	//x轴逆时针倾斜a°等价于把点全部顺时针旋转弧度a/180*PIq[i] = rotate(q[i], a / 180 * PI);q[i].x /= p;//坐标仿射变换}random_shuffle(q, q + n);Circle c({q[0], 0});for (int i = 1; i < n; i ++ )if (dcmp(c.r, get_dist(c.p, q[i])) < 0){c = {q[i], 0};for (int j = 0; j < i; j ++ )if (dcmp(c.r, get_dist(c.p, q[j])) < 0){c = {(q[i] + q[j]) / 2, get_dist(q[i], q[j]) / 2};for (int k = 0; k < j; k ++ )if (dcmp(c.r, get_dist(c.p, q[k])) < 0)c = get_circle(q[i], q[j], q[k]);}}printf("%.3lf\n", c.r);return 0;
}

三维凸包

  1. 三维向量表示(x, y, z)
  2. 向量加减法、数乘运算，与二维相同
  3. 模长 |A| = sqrt(x * x + y * y + z * z)
  4. 点积
    (1) 几何意义：A·B = |A| * |B| * cos©
    (2) 代数求解：(x1, y1, z1) · (x2, y2, z2) = (x1x2, y1y2, z1z2);
  5. 叉积
    (1) 几何意义：AxB = |A| * |B| * sin©，方向：右手定则
    (2) 代数求解：AxB = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - x2y1)
  6. 如何求平面法向量
    任取平面上两个不共线的向量A、B：AxB
  7. 判断点D是否在平面里
    任取平面上两个不共线的向量A、B：先求法向量C = AxB，然后求平面上任意一点到D的向量E与C的点积，判断点积是否为0。
  8. 求点D到平面的距离
    任取平面上两个不共线的向量A、B：先求法向量C = AxB。然后求平面上任意一点到D的向量E在C上的投影长度即可。即：E·C / |C|
  9. 多面体欧拉定理
    顶点数 - 棱长数 + 表面数 = 2
  10. 三维凸包

2119. 最佳包裹

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int N = 210;
const double eps = 1e-12;int n, m;
bool g[N][N];double rand_eps()
{return ((double)rand() / RAND_MAX - 0.5) * eps;
}struct Point
{double x, y, z;void shake(){x += rand_eps(), y += rand_eps(), z += rand_eps();}Point operator- (Point t){return {x - t.x, y - t.y, z - t.z};}double operator& (Point t){return x * t.x + y * t.y + z * t.z;}Point operator* (Point t){return {y * t.z - t.y * z, z * t.x - x * t.z, x * t.y - y * t.x};}double len(){return sqrt(x * x + y * y + z * z);}
}q[N];
struct Plane
{int v[3];Point norm()  // 法向量{return (q[v[1]] - q[v[0]]) * (q[v[2]] - q[v[0]]);}double area()  // 求面积{return norm().len() / 2;}bool above(Point a){return ((a - q[v[0]]) & norm()) >= 0;}
}plane[N], np[N];void get_convex_3d()
{plane[m ++ ] = {0, 1, 2};plane[m ++ ] = {2, 1, 0};for (int i = 3; i < n; i ++ ){int cnt = 0;for (int j = 0; j < m; j ++ ){bool t = plane[j].above(q[i]);if (!t) np[cnt ++ ] = plane[j];for (int k = 0; k < 3; k ++ )g[plane[j].v[k]][plane[j].v[(k + 1) % 3]] = t;}for (int j = 0; j < m; j ++ )for (int k = 0; k < 3; k ++ ){int a = plane[j].v[k], b = plane[j].v[(k + 1) % 3];if (g[a][b] && !g[b][a])np[cnt ++ ] = {a, b, i};}m = cnt;for (int j = 0; j < m; j ++ ) plane[j] = np[j];}
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ){scanf("%lf%lf%lf", &q[i].x, &q[i].y, &q[i].z);q[i].shake();}get_convex_3d();double res = 0;for (int i = 0; i < m; i ++ )res += plane[i].area();printf("%lf\n", res);return 0;
}

在这里插入图片描述

旋转卡壳

求出凸包之后
双指针算法使得旋转卡壳是O（n）的线性复杂度

int rotating_calipers()
{if (top <= 2) return get_dist(q[0], q[n - 1]);int res = 0;for (int i = 0, j = 2; i < top; i ++ ){auto d = q[stk[i]], e = q[stk[i + 1]];//i在移动的时候，j不断走到最远while (area(d, e, q[stk[j]]) < area(d, e, q[stk[j + 1]])) j = (j + 1) % top;res = max(res, max(get_dist(d, q[stk[j]]), get_dist(e, q[stk[j]])));}return res;
}

2938. 周游世界

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;
const int N = 50010;int n;
PII q[N];
int stk[N], top;
bool used[N];PII operator- (PII a, PII b)
{return {a.x - b.x, a.y - b.y};
}int operator* (PII a, PII b)
{return a.x * b.y - a.y * b.x;
}int area(PII a, PII b, PII c)
{return (b - a) * (c - a);
}int get_dist(PII a, PII b)
{int dx = a.x - b.x;int dy = a.y - b.y;return dx * dx + dy * dy;
}void get_convex()
{sort(q, q + n);for (int i = 0; i < n; i ++ ){while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0){if (area(q[stk[top - 2]], q[stk[top - 1]], q[i]) < 0)used[stk[ -- top]] = false;else top -- ;}stk[top ++ ] = i;used[i] = true;}used[0] = false;for (int i = n - 1; i >= 0; i -- ){if (used[i]) continue;while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0)top -- ;stk[top ++ ] = i;}top -- ;
}int rotating_calipers()
{if (top <= 2) return get_dist(q[0], q[n - 1]);int res = 0;for (int i = 0, j = 2; i < top; i ++ ){auto d = q[stk[i]], e = q[stk[i + 1]];while (area(d, e, q[stk[j]]) < area(d, e, q[stk[j + 1]])) j = (j + 1) % top;res = max(res, max(get_dist(d, q[stk[j]]), get_dist(e, q[stk[j]])));}return res;
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d%d", &q[i].x, &q[i].y);get_convex();printf("%d\n", rotating_calipers());return 0;
}作者：yxc
链接：https://www.acwing.com/activity/content/code/content/646529/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

注意，当所有点共线时，求得的凸包只包含起点，但并不影响求最远点对，因为代码第70行特判了所有点共线的情况。另外如果打算求所有点共线的凸包，可以将代码第60行的小于等于号变成小于号。

2142. 最小矩形覆盖

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 50010;
const double eps = 1e-12, INF = 1e20;
const double PI = acos(-1);int n;
PDD q[N];
PDD ans[N];
double min_area = INF;
int stk[N], top;
bool used[N];int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}PDD operator+ (PDD a, PDD b)
{return {a.x + b.x, a.y + b.y};
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}PDD operator* (PDD a, double t)
{return {a.x * t, a.y * t};
}PDD operator/ (PDD a, double t)
{return {a.x / t, a.y / t};
}double operator* (PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double operator& (PDD a, PDD b)
{return a.x * b.x + a.y * b.y;
}double area(PDD a, PDD b, PDD c)
{return (b - a) * (c - a);
}double get_len(PDD a)
{return sqrt(a & a);
}double project(PDD a, PDD b, PDD c)
{return ((b - a) & (c - a)) / get_len(b - a);
}PDD norm(PDD a)
{return a / get_len(a);
}PDD rotate(PDD a, double b)
{return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}void get_convex()
{sort(q, q + n);for (int i = 0; i < n; i ++ ){while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0)used[stk[ -- top]] = false;stk[top ++ ] = i;used[i] = true;}used[0] = false;for (int i = n - 1; i >= 0; i -- ){if (used[i]) continue;while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0)top -- ;stk[top ++ ] = i;}reverse(stk, stk + top);top -- ;
}void rotating_calipers()
{for (int i = 0, a = 2, b = 1, c = 2; i < top; i ++ ){auto d = q[stk[i]], e = q[stk[i + 1]];while (dcmp(area(d, e, q[stk[a]]), area(d, e, q[stk[a + 1]])) < 0) a = (a + 1) % top;while (dcmp(project(d, e, q[stk[b]]), project(d, e, q[stk[b + 1]])) < 0) b = (b + 1) % top;if (!i) c = a;while (dcmp(project(d, e, q[stk[c]]), project(d, e, q[stk[c + 1]])) > 0) c = (c + 1) % top;auto x = q[stk[a]], y = q[stk[b]], z = q[stk[c]];auto h = area(d, e, x) / get_len(e - d);auto w = ((y - z) & (e - d)) / get_len(e - d);if (h * w < min_area){min_area = h * w;ans[0] = d + norm(e - d) * project(d, e, y);ans[3] = d + norm(e - d) * project(d, e, z);auto u = norm(rotate(e - d, -PI / 2));ans[1] = ans[0] + u * h;ans[2] = ans[3] + u * h;}}
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);get_convex();rotating_calipers();int k = 0;for (int i = 1; i < 4; i ++ )if (dcmp(ans[i].y, ans[k].y) < 0 || !dcmp(ans[i].y, ans[k].y) && dcmp(ans[i].x, ans[k].x))k = i;printf("%.5lf\n", min_area);for (int i = 0; i < 4; i ++, k ++ ){auto x = ans[k % 4].x, y = ans[k % 4].y;if (!sign(x)) x = 0;if (!sign(y)) y = 0;printf("%.5lf %.5lf\n", x, y);}return 0;
}

三角剖分

三角剖分思想模板题
本题求圆与某一多边形的交的面积

分析：
将多边形的各个端点按逆时针方向做向量
再将圆心与多边形的每个顶点连边，求出相邻两点与圆心构成三角形的面积，因为有方向，因此红色代表负面积，绿色代表正面积。
正：AOB、BOC
负：AOD、COD
再分别描出红色部分与圆的交，绿色部分与圆的交。
发现所求部分就是绿色部分与圆的交的面积+红色部分与圆的交的部分（因为是负数）
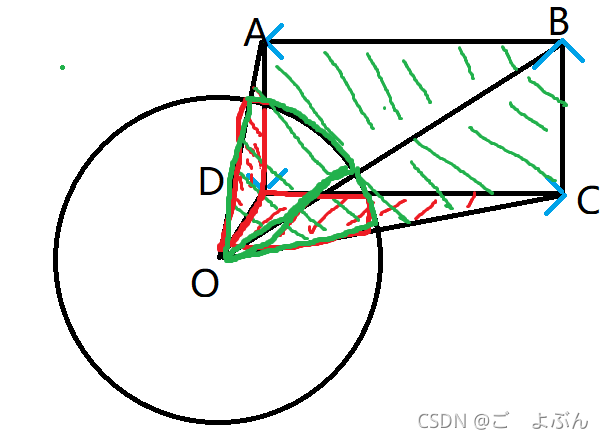
QQ截图20210810223436.png

做法：
最终目标：需求出多边形所有相邻两点与原点构成的三角形与圆的交的部分的面积的和即可。
现在的需要解决的就是如何求出三角形与圆的交的面积，分情况讨论：

返回三角形面积
返回扇形部分
求出交点Pb，返回三角形rPba和扇形面积
求出线段ab与圆的交点Pa，返回三角形rPab和扇形面积
求出线段ab与圆的交点Pa和Pb，返回左右两个扇形和三角形ParPb的面积
1.png
如何区别每种情况：
三点共线，即构成三角形面积为0，直接返回0

  1. a和b到圆心的距离均小于R，则为第一种情况
  2. 圆心到线段的距离大于等于半径，则为第二种情况
  3. a到圆心的距离小于等于半径，则为第三种情况
  4. b到圆心的距离小于等于半径，则为第四种情况
  5. 其余则为第四种情况

如何求出点到线段距离以及如何求出直线与圆的交点？
过圆心先做线段ab所在直线的垂线re，求出re的长度，若点e在不线段ab上，说明垂线长度并不是点到线段真实距离，点a和b到圆心的距离较小值才是。
已经求出e，再通过旋转re可以求出ea的方向向量，也就能求出点交点坐标。
QQ截图20210810231257.png

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 55;
const double eps = 1e-8;
const double PI = acos(-1);double R;
int n;
PDD q[N], r;int sign(double x)
{if (fabs(x) < eps) return 0;return x < 0 ? -1 : 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;return x < y ? -1 : 1;
}PDD operator+ (PDD a, PDD b) { return {a.x + b.x, a.y + b.y}; }
PDD operator- (PDD a, PDD b) { return {a.x - b.x, a.y - b.y}; }
PDD operator* (PDD a, double b) { return {a.x * b, a.y * b}; }
PDD operator/ (PDD a, double b) { return {a.x / b, a.y / b}; }
double operator* (PDD a, PDD b) { return {a.x * b.y - a.y * b.x}; }
double operator& (PDD a, PDD b) { return {a.x * b.x + a.y * b.y}; }
double area(PDD a, PDD b, PDD c) { return (b - a) * (c - a); }
double get_len(PDD a) { return sqrt(a & a); }
double get_dist(PDD a, PDD b) { return get_len(b - a); }
double project(PDD a, PDD b, PDD c) { return ((c - a) & (b - a)) / get_len(b - a); }
PDD rotate(PDD a, double b) { return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)}; }
PDD norm(PDD a) { return a / get_len(a); }
bool on_segment(PDD p, PDD a, PDD b) { return !sign((p - a) * (p - b)) && sign((p - a) & (p - b)) <= 0; }PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) // 求两直线交点
{auto u = p - q;double t = (w * u) / (v * w);return p + v * t;
}double get_circle_line_intersection(PDD a, PDD b, PDD& pa, PDD& pb) // 求圆与线段ab的交点，并返回点到线段距离
{auto e = get_line_intersection(a, b - a, r, rotate(b - a, PI / 2));auto mind = get_dist(r, e);if (!on_segment(e, a, b)) mind = min(get_dist(r, a), get_dist(r, b));if (dcmp(R, mind) <= 0) return mind;auto len = sqrt(R * R - get_dist(r, e) * get_dist(r, e));pa = e + norm(a - b) * len;pb = e + norm(b - a) * len;return mind;
}double get_sector(PDD a, PDD b) //求扇形面积
{auto angle = acos((a & b) / get_len(a) / get_len(b));if (sign(a * b) < 0) angle *= -1;return R * R * angle / 2;
}double get_circle_triangle_area(PDD a, PDD b) // 求圆与三角形相交部分面积
{auto da = get_dist(r, a), db = get_dist(r, b);if (dcmp(R, da) >= 0 && dcmp(R, db) >= 0) return a * b / 2;if (!sign(a * b)) return 0;PDD pa, pb;  //  直线与圆的交点auto mind = get_circle_line_intersection(a, b, pa, pb);if (dcmp(R, mind) <= 0) return get_sector(a, b);if (dcmp(R, da) >= 0) return a * pb / 2 + get_sector(pb, b);if (dcmp(R, db) >= 0) return pa * b / 2 + get_sector(a, pa);return get_sector(pb, b) + pa * pb / 2 + get_sector(a, pa);
}double work()
{double res = 0;for (int i = 0; i < n; i++) // 求出多边形所有相邻两点与原点构成的三角形与圆的交的部分的面积的和res += get_circle_triangle_area(q[i], q[(i + 1) % n]);return fabs(res); // 因为顶点给定顺序是不确定的，因此需要输出绝对值
}int main()
{while (cin >> R >> n){for (int i = 0; i < n; i++)  cin >> q[i].x >> q[i].y;printf("%.2lf\n", work());}
}

3034. 望远镜

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 55;
const double eps = 1e-8;
const double PI = acos(-1);double R;
int n;
PDD q[N], r;int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}PDD operator+ (PDD a, PDD b)
{return {a.x + b.x, a.y + b.y};
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}PDD operator* (PDD a, double t)
{return {a.x * t, a.y * t};
}PDD operator/ (PDD a, double t)
{return {a.x / t, a.y / t};
}double operator* (PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double operator& (PDD a, PDD b)
{return a.x * b.x + a.y * b.y;
}double area(PDD a, PDD b, PDD c)
{return (b - a) * (c - a);
}double get_len(PDD a)
{return sqrt(a & a);
}double get_dist(PDD a, PDD b)
{return get_len(b - a);
}double project(PDD a, PDD b, PDD c)
{return ((c - a) & (b - a)) / get_len(b - a);
}PDD rotate(PDD a, double b)
{return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}PDD norm(PDD a)
{return a / get_len(a);
}bool on_segment(PDD p, PDD a, PDD b)
{return !sign((p - a) * (p - b)) && sign((p - a) & (p - b)) <= 0;
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{auto u = p - q;auto t = w * u / (v * w);return p + v * t;
}double get_circle_line_intersection(PDD a, PDD b, PDD& pa, PDD& pb)
{auto e = get_line_intersection(a, b - a, r, rotate(b - a, PI / 2));auto mind = get_dist(r, e);if (!on_segment(e, a, b)) mind = min(get_dist(r, a), get_dist(r, b));if (dcmp(R, mind) <= 0) return mind;auto len = sqrt(R * R - get_dist(r, e) * get_dist(r, e));pa = e + norm(a - b) * len;pb = e + norm(b - a) * len;return mind;
}double get_sector(PDD a, PDD b)
{auto angle = acos((a & b) / get_len(a) / get_len(b));if (sign(a * b) < 0) angle = -angle;return R * R * angle / 2;
}double get_circle_triangle_area(PDD a, PDD b)
{auto da = get_dist(r, a), db = get_dist(r, b);if (dcmp(R, da) >= 0 && dcmp(R, db) >= 0) return a * b / 2;if (!sign(a * b)) return 0;PDD pa, pb;auto mind = get_circle_line_intersection(a, b, pa, pb);if (dcmp(R, mind) <= 0) return get_sector(a, b);if (dcmp(R, da) >= 0) return a * pb / 2 + get_sector(pb, b);if (dcmp(R, db) >= 0) return get_sector(a, pa) + pa * b / 2;return get_sector(a, pa) + pa * pb / 2 + get_sector(pb, b);
}double work()
{double res = 0;for (int i = 0; i < n; i ++ )res += get_circle_triangle_area(q[i], q[(i + 1) % n]);return fabs(res);
}int main()
{while (scanf("%lf%d", &R, &n) != -1){for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);printf("%.2lf\n", work());}return 0;
}

扫描线

3068. 扫描线

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>#define x first
#define y secondusing namespace std;typedef long long LL;
typedef pair<int, int> PII;
const int N = 1010;int n;
PII l[N], r[N];
PII q[N];LL range_area(int a, int b)
{int cnt = 0;for (int i = 0; i < n; i ++ )if (l[i].x <= a && r[i].x >= b)q[cnt ++ ] = {l[i].y, r[i].y};if (!cnt) return 0;sort(q, q + cnt);LL res = 0;int st = q[0].x, ed = q[0].y;for (int i = 1; i < cnt; i ++ )if (q[i].x <= ed) ed = max(ed, q[i].y);else{res += ed - st;st = q[i].x, ed = q[i].y;}res += ed - st;return res * (b - a);
}int main()
{scanf("%d", &n);vector<int> xs;for (int i = 0; i < n; i ++ ){scanf("%d%d%d%d", &l[i].x, &l[i].y, &r[i].x, &r[i].y);xs.push_back(l[i].x), xs.push_back(r[i].x);}sort(xs.begin(), xs.end());LL res = 0;for (int i = 0; i + 1 < xs.size(); i ++ )if (xs[i] != xs[i + 1])res += range_area(xs[i], xs[i + 1]);printf("%lld\n", res);return 0;
}

247. 亚特兰蒂斯

在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 100010;int n;
struct Segment
{double x, y1, y2;int k;bool operator< (const Segment &t)const{return x < t.x;}
}seg[N * 2];
struct Node
{int l, r;int cnt;double len;
}tr[N * 8];vector<double> ys;int find(double y)
{return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}void pushup(int u)
{if (tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];else if (tr[u].l != tr[u].r){tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;}else tr[u].len = 0;
}void build(int u, int l, int r)
{tr[u] = {l, r, 0, 0};if (l != r){int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);}
}void modify(int u, int l, int r, int k)
{if (tr[u].l >= l && tr[u].r <= r){tr[u].cnt += k;pushup(u);}else{int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, k);if (r > mid) modify(u << 1 | 1, l, r, k);pushup(u);}
}int main()
{int T = 1;while (scanf("%d", &n), n){ys.clear();for (int i = 0, j = 0; i < n; i ++ ){double x1, y1, x2, y2;scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);seg[j ++ ] = {x1, y1, y2, 1};seg[j ++ ] = {x2, y1, y2, -1};ys.push_back(y1), ys.push_back(y2);}sort(ys.begin(), ys.end());ys.erase(unique(ys.begin(), ys.end()), ys.end());build(1, 0, ys.size() - 2);sort(seg, seg + n * 2);double res = 0;for (int i = 0; i < n * 2; i ++ ){if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);}printf("Test case #%d\n", T ++ );printf("Total explored area: %.2lf\n\n", res);}return 0;
}

2801. 三角形面积并

在这里插入图片描述
时间复杂度是n^3 logn

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 110;
const double eps = 1e-8, INF = 1e6;int n;
PDD tr[N][3];
PDD q[N];int sign(double x)
{if (fabs(x) < eps) return 0;if (x < 0) return -1;return 1;
}int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}PDD operator+ (PDD a, PDD b)
{return {a.x + b.x, a.y + b.y};
}PDD operator- (PDD a, PDD b)
{return {a.x - b.x, a.y - b.y};
}PDD operator* (PDD a, double t)
{return {a.x * t, a.y * t};
}double operator* (PDD a, PDD b)
{return a.x * b.y - a.y * b.x;
}double operator& (PDD a, PDD b)
{return a.x * b.x + a.y * b.y;
}bool on_segment(PDD p, PDD a, PDD b)
{return sign((p - a) & (p - b)) <= 0;
}PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{if (!sign(v * w)) return {INF, INF};auto u = p - q;auto t = w * u / (v * w);auto o = p + v * t;if (!on_segment(o, p, p + v) || !on_segment(o, q, q + w))return {INF, INF};return o;
}double line_area(double a, int side)
{int cnt = 0;for (int i = 0; i < n; i ++ ){auto t = tr[i];if (dcmp(t[0].x, a) > 0 || dcmp(t[2].x, a) < 0) continue;if (!dcmp(t[0].x, a) && !dcmp(t[1].x, a)){if (side) q[cnt ++ ] = {t[0].y, t[1].y};}else if (!dcmp(t[2].x, a) && !dcmp(t[1].x, a)){if (!side) q[cnt ++ ] = {t[2].y, t[1].y};}else{double d[3];int u = 0;for (int j = 0; j < 3; j ++ ){auto o = get_line_intersection(t[j], t[(j + 1) % 3] - t[j], {a, -INF}, {0, INF * 2});if (dcmp(o.x, INF))d[u ++ ] = o.y;}if (u){sort(d, d + u);q[cnt ++ ] = {d[0], d[u - 1]};}}}if (!cnt) return 0;for (int i = 0; i < cnt; i ++ )if (q[i].x > q[i].y)swap(q[i].x, q[i].y);sort(q, q + cnt);double res = 0, st = q[0].x, ed = q[0].y;for (int i = 1; i < cnt; i ++ )if (q[i].x <= ed) ed = max(ed, q[i].y);else{res += ed - st;st = q[i].x, ed = q[i].y;}res += ed - st;return res;
}double range_area(double a, double b)
{return (line_area(a, 1) + line_area(b, 0)) * (b - a) / 2;
}int main()
{scanf("%d", &n);vector<double> xs;for (int i = 0; i < n; i ++ ){for (int j = 0; j < 3; j ++ ){scanf("%lf%lf", &tr[i][j].x, &tr[i][j].y);xs.push_back(tr[i][j].x);}sort(tr[i], tr[i] + 3);}for (int i = 0; i < n; i ++ )for (int j = i + 1; j < n; j ++ )for (int x = 0; x < 3; x ++ )for (int y = 0; y < 3; y ++ ){auto o = get_line_intersection(tr[i][x], tr[i][(x + 1) % 3] - tr[i][x],tr[j][y], tr[j][(y + 1) % 3] - tr[j][y]);if (dcmp(o.x, INF))xs.push_back(o.x);}sort(xs.begin(), xs.end());double res = 0;for (int i = 0; i + 1 < xs.size(); i ++ )if (dcmp(xs[i], xs[i + 1]))res += range_area(xs[i], xs[i + 1]);printf("%.2lf\n", res);return 0;
}

自适应辛普森积分

把曲线变成二次函数
三个点确定二次函数(f(l) + 4 * f(mid) + f®) / 6 （这个是要背的

const double eps = 1e-12;double f(double x)
{return ?
}double simpson(double l, double r)
{auto mid = (l + r) / 2;return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}double asr(double l, double r, double s)
{auto mid = (l + r) / 2;auto left = simpson(l, mid), right = simpson(mid, r);if (fabs(left + right - s) < eps) return left + right;return asr(l, mid, left) + asr(mid, r, right);
}

3074. 自适应辛普森积分

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const double eps = 1e-12;double f(double x)
{return sin(x) / x;
}double simpson(double l, double r)
{auto mid = (l + r) / 2;return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}double asr(double l, double r, double s)
{auto mid = (l + r) / 2;auto left = simpson(l, mid), right = simpson(mid, r);if (fabs(left + right - s) < eps) return left + right;return asr(l, mid, left) + asr(mid, r, right);
}int main()
{double l, r;scanf("%lf%lf", &l, &r);printf("%lf\n", asr(l, r, simpson(l, r)));return 0;
}

3069. 圆的面积并

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;
const int N = 1010;
const double eps = 1e-8;int n;
struct Circle
{PDD r;double R;
}c[N];
PDD q[N];int dcmp(double x, double y)
{if (fabs(x - y) < eps) return 0;if (x < y) return -1;return 1;
}double f(double x)
{int cnt = 0;for (int i = 0; i < n; i ++ ){auto X = fabs(x - c[i].r.x), R = c[i].R;if (dcmp(X, R) < 0){auto Y = sqrt(R * R - X * X);q[cnt ++ ] = {c[i].r.y - Y, c[i].r.y + Y};}}if (!cnt) return 0;sort(q, q + cnt);double res = 0, st = q[0].x, ed = q[0].y;for (int i = 1; i < cnt; i ++ )if (q[i].x <= ed) ed = max(ed, q[i].y);else{res += ed - st;st = q[i].x, ed = q[i].y;}return res + ed - st;
}double simpson(double l, double r)
{auto mid = (l + r) / 2;return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}double asr(double l, double r, double s)
{auto mid = (l + r) / 2;auto left = simpson(l, mid), right = simpson(mid, r);if (fabs(s - left - right) < eps) return left + right;return asr(l, mid, left) + asr(mid, r, right);
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ )scanf("%lf%lf%lf", &c[i].r.x, &c[i].r.y, &c[i].R);double l = -2000, r = 2000;printf("%.3lf\n", asr(l, r, simpson(l, r)));return 0;
}

这篇关于计算几何(基础知识凸包半平面交最小圆覆盖三维计算几何基础 三维凸包 旋转卡壳三角剖分扫描线自适应辛普森积分的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/202239。

相关文章

linux-基础知识3

linux-基础知识3

打包和压缩 zip 安装zip软件包 yum -y install zip unzip 压缩打包命令: zip -q -r -d -u 压缩包文件名 目录和文件名列表 -q:不显示命令执行过程-r:递归处理，打包各级子目录和文件-u:把文件增加/替换到压缩包中-d:从压缩包中删除指定的文件 解压:unzip 压缩包名 打包文件 把压缩包从服务器下载到本地 把压缩包上传到服务器(zip
阅读更多...
hdu1240、hdu1253（三维搜索题）

hdu1240、hdu1253（三维搜索题）

1、从后往前输入，（x，y，z）; 2、从下往上输入，（y , z, x）; 3、从左往右输入，（z，x，y）； hdu1240代码如下： #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#inc
阅读更多...
hdu4826（三维DP）

hdu4826（三维DP）

这是一个百度之星的资格赛第四题 题目链接：http://acm.hdu.edu.cn/contests/contest_showproblem.php?pid=1004&cid=500 题意：从左上角的点到右上角的点，每个点只能走一遍，走的方向有三个：向上，向下，向右，求最大值。 咋一看像搜索题，先暴搜，TLE,然后剪枝，还是TLE.然后我就改方法，用DP来做，这题和普通dp相比，多个个向上
阅读更多...
计组基础知识

计组基础知识

操作系统的特征 并发共享虚拟异步 操作系统的功能 1、资源分配，资源回收硬件资源 CPU、内存、硬盘、I/O设备。2、为应⽤程序提供服务操作系统将硬件资源的操作封装起来，提供相对统⼀的接⼝（系统调⽤）供开发者调⽤。3、管理应⽤程序即控制进程的⽣命周期：进程开始时的环境配置和资源分配、进程结束后的资源回收、进程调度等。4、操作系统内核的功能（1）进程调度能⼒： 管理进程、线
阅读更多...
零基础学习Redis(10) -- zset类型命令使用

零基础学习Redis(10) -- zset类型命令使用

zset是有序集合，内部除了存储元素外，还会存储一个score，存储在zset中的元素会按照score的大小升序排列，不同元素的score可以重复，score相同的元素会按照元素的字典序排列。 1. zset常用命令 1.1 zadd  zadd key [NX | XX] [GT | LT]   [CH] [INCR] score member [score member ...]
阅读更多...
poj 1258 Agri-Net（最小生成树模板代码）

poj 1258 Agri-Net（最小生成树模板代码）

感觉用这题来当模板更适合。 题意就是给你邻接矩阵求最小生成树啦。~ prim代码：效率很高。172k...0ms。 #include<stdio.h>#include<algorithm>using namespace std;const int MaxN = 101;const int INF = 0x3f3f3f3f;int g[MaxN][MaxN];int n
阅读更多...
poj 1287 Networking（prim or kruscal最小生成树）

poj 1287 Networking（prim or kruscal最小生成树）

题意给你点与点间距离，求最小生成树。 注意点是，两点之间可能有不同的路，输入的时候选择最小的，和之前有道最短路WA的题目类似。 prim代码： #include<stdio.h>const int MaxN = 51;const int INF = 0x3f3f3f3f;int g[MaxN][MaxN];int P;int prim(){bool vis[MaxN];
阅读更多...
poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

题目很麻烦，因为不熟悉最小生成树的算法调试了好久。 感觉网上的题目解释都没说得很清楚，不适合新手。自己写一个。 题意：给你点的坐标，然后两点间可以有两种方式来通信：第一种是卫星通信，第二种是无线电通信。 卫星通信：任何两个有卫星频道的点间都可以直接建立连接，与点间的距离无关； 无线电通信：两个点之间的距离不能超过D，无线电收发器的功率越大，D越大，越昂贵。 计算无线电收发器D
阅读更多...
uva 10387 Billiard（简单几何）

uva 10387 Billiard（简单几何）

题意是一个球从矩形的中点出发，告诉你小球与矩形两条边的碰撞次数与小球回到原点的时间，求小球出发时的角度和小球的速度。 简单的几何问题，小球每与竖边碰撞一次，向右扩展一个相同的矩形；每与横边碰撞一次，向上扩展一个相同的矩形。 可以发现，扩展矩形的路径和在当前矩形中的每一段路径相同，当小球回到出发点时，一条直线的路径刚好经过最后一个扩展矩形的中心点。 最后扩展的路径和横边竖边恰好组成一个直
阅读更多...
poj 1734 （floyd求最小环并打印路径）

poj 1734 （floyd求最小环并打印路径）

题意： 求图中的一个最小环，并打印路径。 解析： ans 保存最小环长度。 一直wa，最后终于找到原因，inf开太大爆掉了。。。 虽然0x3f3f3f3f用memset好用，但是还是有局限性。 代码： #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#incl
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2