卡壳专题
uva 12307 - Smallest Enclosing Rectangle(旋转卡壳)
题目链接:uva 12307 - Smallest Enclosing Rectangle 两组踵对点围成长方形,枚举出所有可行长方形维护最小值。 #include <cstdio>#include <cstring>#include <cmath>#include <vector>#include <complex>#include <algorithm>using
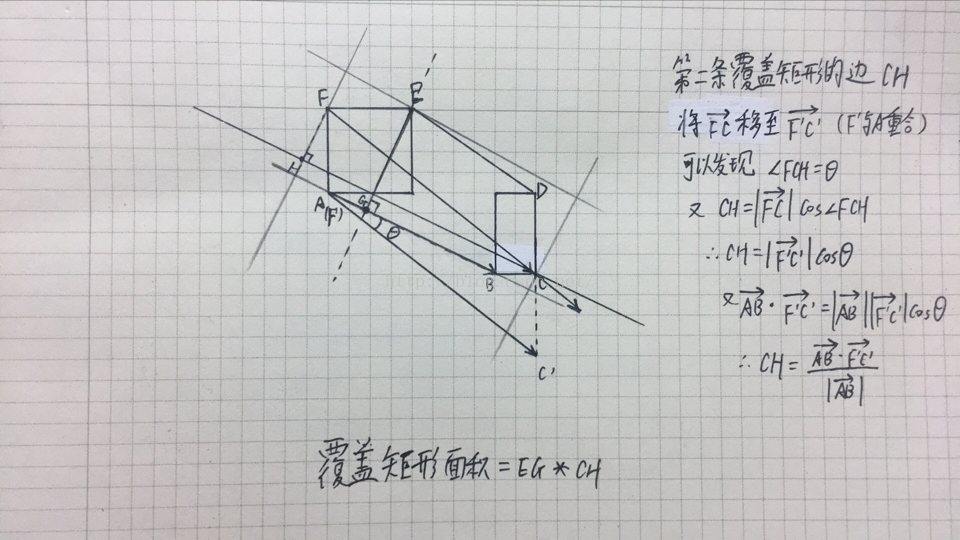
HDU 5251 矩形面积 (最小矩形覆盖 凸包+旋转卡壳 详解 推荐)
矩形面积 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 408 Accepted Submission(s): 232 Problem Description 小度熊有一个桌面,小度熊剪了很多矩形放在桌面上,
POJ 2187 Beauty Contest (凸包最远点距旋转卡壳)
http://poj.org/problem?id=2187 思路:算出凸包后枚举凸包上的点。复杂度为O(NlogN+M) 为什么可以枚举? 设坐标的绝对值不超过M,则凸包至多有O(√M)个顶点 证明:以(0,0)为起点画出如下“极限凸包” (0,0)-(1,0)-(2,1)-(3,3)-(4,6)-...当x每次只增加1时,y增加速率是平方级的,所以凸包至多有O(√M)个顶点。
凸包及旋转卡壳求凸包直径
那么,先提一下最基本最暴力的求凸包直径的方法吧---枚举。。。好吧。。很多问题都可以用 枚举 这个“万能”的方法来解决,过程很简单方便是肯定的,不过在效率上就要差很远了。 要求一个点集的直径,即使先计算出这个点集的凸包,然后再枚举凸包上的点对,这样来求点集直径的话依然会在凸包上点的数量达到O(n)级别是极大的降低它的效率,也浪费了凸包的优美性质。不过在数据量较小或者很适合时,何必要大费周折的用那些
破阵子(三分+凸包旋转卡壳)
Description 平面上有n个点,每个点有各自的速度向量,现在给出0时刻,在同一时刻,平面点的最远距离叫做special dis他们每个点的位置和每个点的速度向量,现在求在哪个时刻的时候,他们的special dis 最小,并输出这个距离。 Input 输入一个正整数T(T<=10),表示有T组数据,每组数据包括一个n(n<=10000),表示有n个点,每行包括每个点的坐标 (x,y
POJ 2187 Beauty Contest (旋转卡壳 最远点对)
http://poj.org/problem?id=2187 题意:给出二维平面上n个点的坐标,求距离最远的点对距离的平方。 显然距离最远的两个点在这些散点的凸包上,然后用旋转卡壳的算法找出最远点对,具体原理参见这位大佬的博客http://www.cnblogs.com/xdruid/archive/2012/07/01/2572303.html 大概是利用凸包上的点依次与对应边产生的距离成
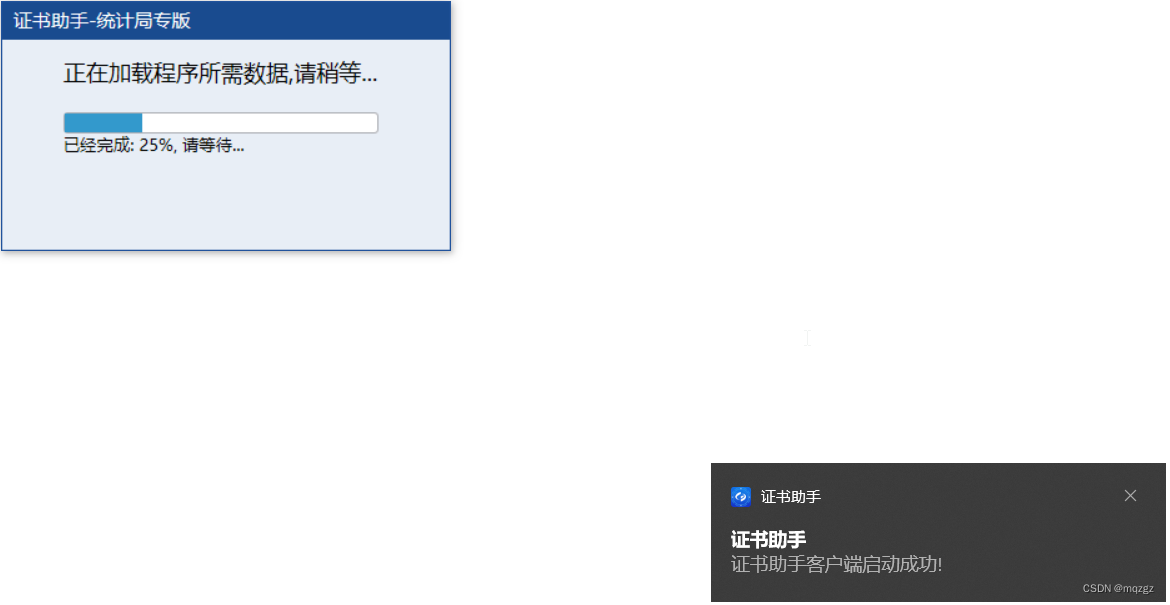
证书助手-统计局专版启动25%卡壳不动
登录国家统计局在线证书验证系统,检查系统环境及证书的时候,一直提示找不到证书助手启动,手动结束证书助手进程重新启动,一直加载到25%无法继续加载。 换浏览器和换网络都不行,清理系统缓存,浏览器缓存不行。最后考虑到了杀毒软件的问题。 把杀毒软件disbale之后,证书助手一下子就加载完成正常启动。证书系统环境检查也一下子通过了。
计算几何(基础知识凸包半平面交最小圆覆盖三维计算几何基础 三维凸包 旋转卡壳三角剖分扫描线自适应辛普森积分
第四章 计算几何 基础知识 前置知识点 (1) pi = acos(-1); (2) 余弦定理 c^2 = a^2 + b^2 - 2abcos(t) 浮点数的比较 const double eps = 1e-8; int sign(double x) // 符号函数 { if (fabs(x) < eps) return 0; if (x < 0) return -1; return 1