本文主要是介绍HDU 5251 矩形面积 (最小矩形覆盖 凸包+旋转卡壳 详解 推荐),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
矩形面积
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 408 Accepted Submission(s): 232
Total Submission(s): 408 Accepted Submission(s): 232
Problem Description
小度熊有一个桌面,小度熊剪了很多矩形放在桌面上,小度熊想知道能把这些矩形包围起来的面积最小的矩形的面积是多少。
第一行一个正整数 T,代表测试数据组数( 1≤T≤20 ),接下来 T 组测试数据。
每组测试数据占若干行,第一行一个正整数 N(1≤N<≤1000) ,代表矩形的数量。接下来 N 行,每行 8 个整数 x1,y1,x2,y2,x3,y3,x4,y4 ,代表矩形的四个点坐标,坐标绝对值不会超过10000。
每组测试数据占若干行,第一行一个正整数 N(1≤N<≤1000) ,代表矩形的数量。接下来 N 行,每行 8 个整数 x1,y1,x2,y2,x3,y3,x4,y4 ,代表矩形的四个点坐标,坐标绝对值不会超过10000。
对于每组测试数据,输出两行:
第一行输出"Case #i:",i 代表第 i 组测试数据。
第二行包含1 个数字,代表面积最小的矩形的面积,结果保留到整数位。
第一行输出"Case #i:",i 代表第 i 组测试数据。
第二行包含1 个数字,代表面积最小的矩形的面积,结果保留到整数位。
2 2 5 10 5 8 3 10 3 8 8 8 8 6 7 8 7 6 1 0 0 2 2 2 0 0 2
Case #1: 17 Case #2: 4
2015年百度之星程序设计大赛 - 初赛(1)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5251
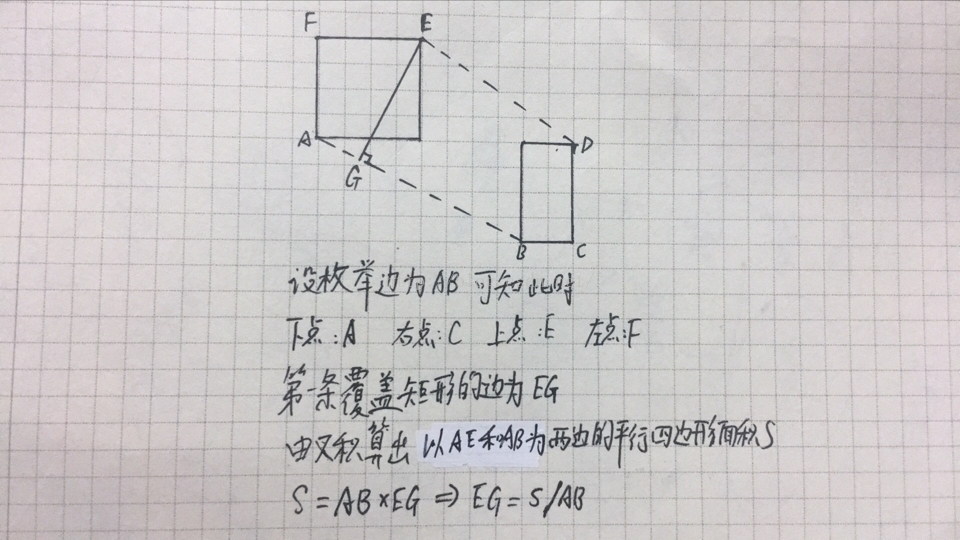
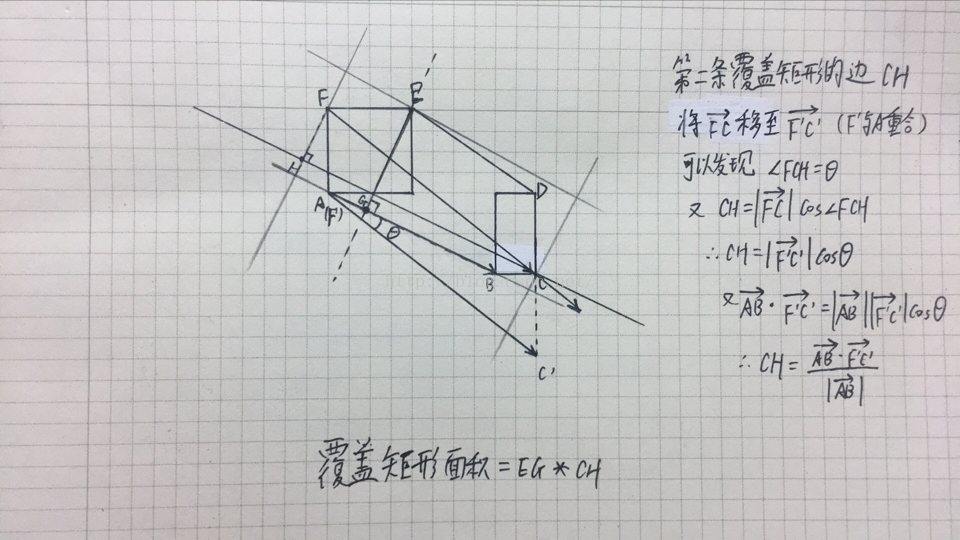
题目分析:很明显就是求所有点围成的凸包的最小矩形覆盖,有一个结论(YY出来的),最小覆盖矩形必有一条边和凸包的一条边重合,graham扫描求出凸包,然后从左下的base点开始逆时针枚举边,用旋转卡壳求其余三边,距离下点向左向右向上分别的最远点,求的时候也按照逆时针的顺序,所以是下->右->上->左,求右点用点积最远的显然|a||b|cosθ的值最大,求上点用叉积,对踵点三角形面积最大,求左点和右点同理,一条边和三个点得到后就可以计算面积了,上点和枚举边的距离是当前覆盖矩形的一条边,这个很容易求,因为叉积算出的是平行四边形的面积,所以直接用叉积的结果除枚举边的边长L 即可,然后另一条覆盖矩形的边利用点积来求,设左点指向右点的向量为vt,将左点移动到枚举边的左端点处得到一个夹角A,由于覆盖矩形的第一条边和枚举边是垂直的,因此第二条边就是|vt|cosθ,因为向量的点积等于两个向量的模长积乘夹角的余弦值,即|vt|*L*cosθ = 点积 => |vt|cosθ = 点积 / L
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5251
题目分析:很明显就是求所有点围成的凸包的最小矩形覆盖,有一个结论(YY出来的),最小覆盖矩形必有一条边和凸包的一条边重合,graham扫描求出凸包,然后从左下的base点开始逆时针枚举边,用旋转卡壳求其余三边,距离下点向左向右向上分别的最远点,求的时候也按照逆时针的顺序,所以是下->右->上->左,求右点用点积最远的显然|a||b|cosθ的值最大,求上点用叉积,对踵点三角形面积最大,求左点和右点同理,一条边和三个点得到后就可以计算面积了,上点和枚举边的距离是当前覆盖矩形的一条边,这个很容易求,因为叉积算出的是平行四边形的面积,所以直接用叉积的结果除枚举边的边长L 即可,然后另一条覆盖矩形的边利用点积来求,设左点指向右点的向量为vt,将左点移动到枚举边的左端点处得到一个夹角A,由于覆盖矩形的第一条边和枚举边是垂直的,因此第二条边就是|vt|cosθ,因为向量的点积等于两个向量的模长积乘夹角的余弦值,即|vt|*L*cosθ = 点积 => |vt|cosθ = 点积 / L


#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
double const INF = 1e40;
int const MAX = 1e3 + 5;
int n, top;
double ans;struct POINT {int x, y;
}p[MAX << 2], stk[MAX << 2], base;double getDist(POINT p1, POINT p2) {return sqrt(1.0 * (p1.x - p2.x) * (p1.x - p2.x) + 1.0 * (p1.y - p2.y) * (p1.y - p2.y));
}int getCross(POINT p0, POINT p1, POINT p2) {return (p1.x - p0.x) * (p2.y - p0.y) - (p2.x - p0.x) * (p1.y - p0.y);
}int getDot(POINT p0, POINT p1, POINT p2) {return (p1.x - p0.x) * (p2.x - p0.x) + (p1.y - p0.y) * (p2.y - p0.y);
}bool cmp(POINT p1, POINT p2) {if (getCross(base, p1, p2) == 0) {return getDist(base, p1) < getDist(base, p2);}if (getCross(base, p1, p2) > 0) {return true;}return false;
}void getBase() {scanf("%d", &n);n = n << 2;scanf("%d %d", &p[0].x, &p[0].y);base.x = p[0].x;base.y = p[0].y;int pos = 0;for (int i = 1; i < n; i ++) {scanf("%d %d", &p[i].x, &p[i].y);if(p[i].y < base.y || (p[i].y == base.y && p[i].x < base.x)) {base.x = p[i].x;base.y = p[i].y;pos = i;}}swap(p[pos], p[0]);
}void getConvex() {sort(p, p + n, cmp);stk[0] = p[0];if (n == 1) {return;}stk[1] = p[1];top = 1;for (int i = 2; i < n; i ++) {while (top > 0 && getCross(stk[top - 1], stk[top], p[i]) <= 0) {top --;}stk[++ top] = p[i];}
}double solve() {ans = INF;int down, left = 0, right = 1, up = 0;stk[++ top] = stk[0];for (down = 0; down < top; down ++) {// find rightwhile (getDot(stk[down], stk[down + 1], stk[right]) <= getDot(stk[down], stk[down + 1], stk[right + 1])) {right = (right + 1) % top;}// find upif(down == 0) {up = right;}while (getCross(stk[down], stk[down + 1], stk[up]) <= getCross(stk[down], stk[down + 1], stk[up + 1])) {up = (up + 1) % top;}//find leftif (down == 0) {left = up;}while (getDot(stk[down], stk[down + 1], stk[left]) >= getDot(stk[down], stk[down + 1], stk[left + 1])) {left = (left + 1) % top;}double dist = getDist(stk[down], stk[down + 1]);double X = getCross(stk[down], stk[down + 1], stk[up]) / dist;POINT tmp;tmp.x = stk[right].x + stk[down].x - stk[left].x;tmp.y = stk[right].y + stk[down].y - stk[left].y;double Y = getDot(stk[down], stk[down + 1], tmp) / dist;ans = min(ans, X * Y);}return ans;
}int main() {int T;scanf("%d", &T);for (int ca = 1; ca <= T; ca ++) {printf("Case #%d:\n", ca);getBase();getConvex();printf("%.f\n", solve());}
}
这篇关于HDU 5251 矩形面积 (最小矩形覆盖 凸包+旋转卡壳 详解 推荐)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






