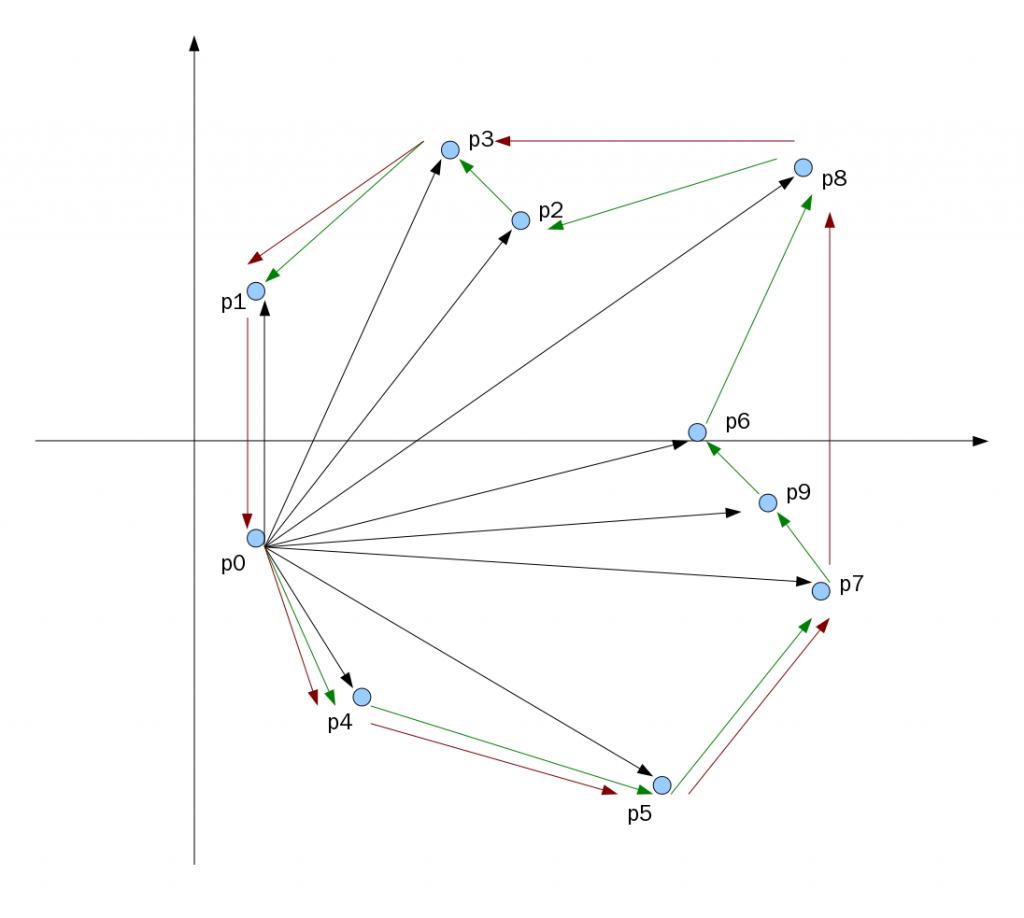
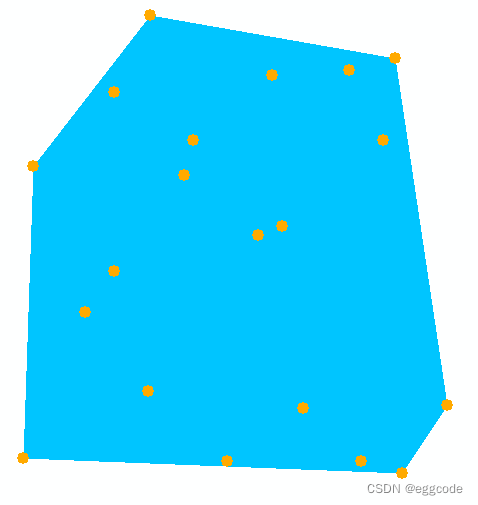
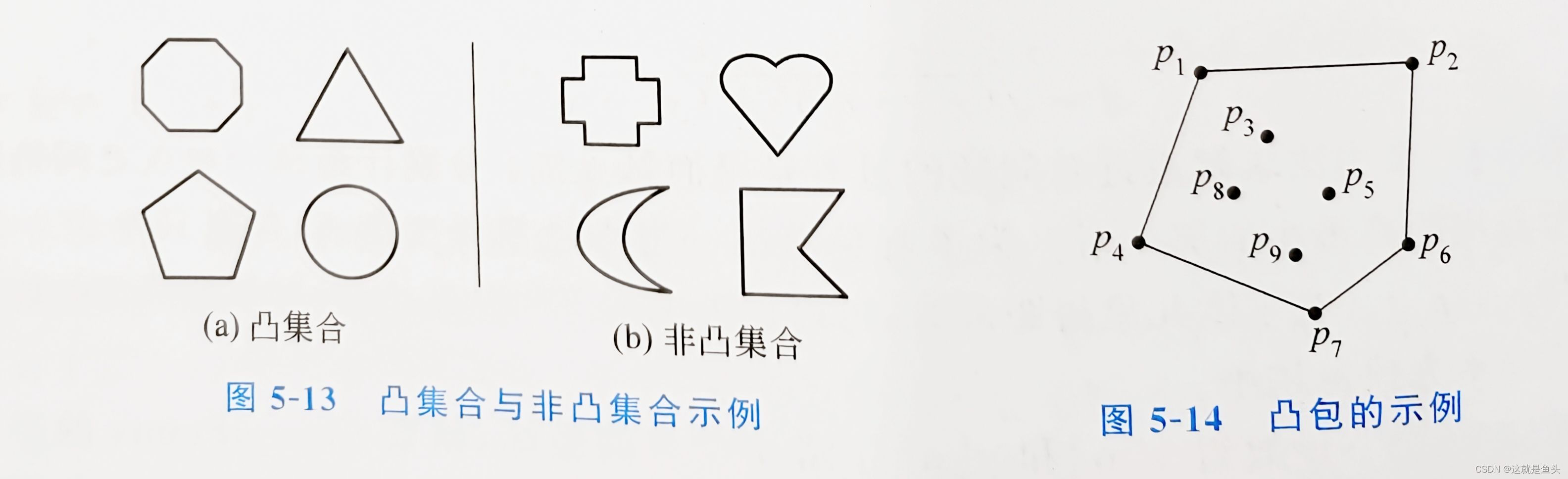
凸包专题

poj 1113 凸包+简单几何计算

题意：给N个平面上的点，现在要在离点外L米处建城墙，使得城墙把所有点都包含进去且城墙的长度最短。解析：韬哥出的某次训练赛上A出的第一道计算几何，算是大水题吧。用convexhull算法把凸包求出来，然后加加减减就A了。计算见下图：好久没玩画图了啊好开心。代码： #include <iostream>#include <cstdio>#inclu

poj 2187 凸包or旋转qia壳法

题意：给n（50000）个点，求这些点与点之间距离最大的距离。解析：先求凸包然后暴力。或者旋转卡壳大法。代码： #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#include <s

Codeforces Beta Round #47 C凸包（最终写法）

题意慢慢看。 typedef long long LL ;int cmp(double x){if(fabs(x) < 1e-8) return 0 ;return x > 0 ? 1 : -1 ;}struct point{double x , y ;point(){}point(double _x , double _y):x(_x) , y(_y){}point op

HDU 1392 HDU 1348 凸包

求凸包的周长，注意n=1 ， 2时特殊情况 int cmp(double x){if(fabs(x) < 1e-8) return 0 ;if(x > 0) return 1 ;return -1 ;}struct point{double x , y ;point(){}point(double _x , double _y):x(_x) , y(_y){}frien

【UVA】10652-Board Wrapping（凸包问题）

又增加了2个模板。 #include <iostream>#include <cstdlib>#include <cstdio>#include <string>#include <cstring>#include <cmath>#include <vector>#include <queue>#include <stack>#include <algorithm>usi

百度之星初赛1006(计算几何:能包含凸包的最小矩形面积)

矩形面积 Accepts: 717 Submissions: 1619 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Problem Description 小度熊有一个桌面，小度熊剪了很多矩形放在桌面上，小度熊想知道能把这些

OpenCV结构分析与形状描述符（8）点集凸包计算函数convexHull()的使用

操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C++11 算法描述查找一个点集的凸包。函数 cv::convexHull 使用斯克拉斯基算法（Sklansky’s algorithm）来查找一个二维点集的凸包，在当前实现中该算法的时间复杂度为 O(N logN)。函数 cv::convexHull 是

OpenCV结构分析与形状描述符（9）检测轮廓相对于其凸包的凹陷缺陷函数convexityDefects()的使用

操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C++11 算法描述查找一个轮廓的凸性缺陷。下图显示了一个手部轮廓的凸性缺陷： convexityDefects 是 OpenCV 库中的一个函数，用于检测轮廓相对于其凸包的凹陷缺陷。这个函数可以帮助识别轮廓中的凹进去的部分，通常被用来分析手部或其他物体的形状

分治算法与凸包问题

1. 什么是凸包问题？凸包问题是计算几何中的经典问题。给定二维平面上的点集，凸包是一个最小的凸多边形，它包含了点集中所有的点。你可以把凸包想象成一根松紧带将所有点紧紧包裹住的样子，凸包的边缘仅沿着最外面的点延伸。 2. 分治法简介分治算法是解决复杂问题的强大策略，它的思想是将问题分解为多个子问题，分别解决这些子问题后再合并得到最终解。凸包问题可以通过分治算法高效地解决，时间复杂度可以达到

$多边形快速凸包算法(Melkman‘s Algorithm)$

多边形快速凸包算法(Melkman‘s Algorithm)

前言平面点集的凸包算法一文介绍了如何计算平面点集或者任意多边形的凸包。对于随机的平面点集，Graham scan和Andraw's 单调链算法已经是最快的算法了。但是对于没有自相交的封闭的简单多边形，存在线性复杂度的算法。下面介绍这一优雅高效的算法。一般的2D凸包算法，首先将点进行排序（时间复杂度）,然后利用栈操作在O(n)的时间复杂度内计算凸包。初始的排序决定了最终的时间复杂度。但是本文

NYOJ 78 圈水池（凸包入门）

链接：click here 题目：有一个牧场，牧场上有很多个供水装置，现在牧场的主人想要用篱笆把这些供水装置圈起来，以防止不是自己的牲畜来喝水，各个水池都标有各自的坐标，现在要你写一个程序利用最短的篱笆将这些供水装置圈起来！（篱笆足够多，并且长度可变）输出各个篱笆经过各个供水装置的坐标点，并且按照x轴坐标值从小到大输出，如果x轴坐标值相同，再安照y轴坐标值从小到大输出样例输入

POJ 2187 Beauty Contest (凸包)

题目地址：POJ 2187 凸包第一发。。用的大白书上的andew算法。先求出凸包，然后最大距离一定是凸包之中的某两点之间的距离，然后枚举找出最大值。代码如下： #include <iostream>#include <cstdio>#include <string>#include <cstring>#include <stdlib.h>#include <math.h

EmguCV学习笔记 VB.Net 6.5 凸包和凸缺陷

AtCoder ABC 365G 凸包 + 二分

题意 AtCoder ABC 365G Freestyle 题解考虑任两种操作 ( A i , B i ) (A_{i},B_{i}) (Ai,Bi)和 ( A j , B j ) (A_{j},B_{j}) (Aj,Bj)，则他们的任意组合可以表示为 ( t A i + ( 1 − t ) A j , t B i + ( 1 − t ) B j ) \big(tA_{i}+(1-

poj2187凸包

今天复习了一下凸包，感觉对于它的理解又加深了，凸包注意的有几点：1基准点在最下面的最左边（习惯性的，注意不只是最下面）2，另外零要重新定义，不再只是一个数，而是一个范围，那么此时对于判零的一系列操作就要注意了，什么时候为右端点，什么时候为左端点，什么时候要进行判零操作等等，3叉乘，要注意与qsort的结合，不要搞混了。下面是这题的代码： #include <iostream>#includ

判断凸包

下面以hdu2108为例，说明一下判断凸包的算法。直接贴此题代码： 232K+15MS #include <stdio.h>#include <stdlib.h>#define Max 1010typedef struct Point{int x;int y;}point;point node[Max];int n;int det(int x1,int y1,int x2,

【NetTopologySuite类库】生成凸包

介绍计算几何体的凸包。凸包是最小的凸几何体，包含输入几何体中的所有点。使用Graham Scan算法。 API地址： https://nettopologysuite.github.io/NetTopologySuite/api/NetTopologySuite.Algorithm.ConvexHull.html 示意图示例代码需在NuGet中安装NetTopologySuit

HDOJ 1348 基本二维凸包问题

这次写的凸包用的是Graham scan算法就数据结构上只是简单地运用了一个栈 #include<stdio.h>#include<cmath>#include<algorithm>//#define LOCALusing namespace std;const int max1=1000;typedef struct point{int x;int y;}point;

uva 11072 - Points（凸包）

题目链接：uva 11072 - Points 求出凸包，判断点是否在凸包内即可。 #include <cstdio>#include <cstring>#include <cmath>#include <vector>#include <complex>#include <algorithm>using namespace std;typedef pair<int

uva 1303 - Wall（凸包）

题目链接：uva 1303 - Wall 求出凸包加个圆周。 #include <cstdio>#include <cstring>#include <cmath>#include <vector>#include <complex>#include <algorithm>using namespace std;typedef pair<int,int> pii;

hdu 5448 Marisa’s Cake（几何+凸包）

题目链接：hdu 5448 Marisa’s Cake 解题思路这题和zoj 3871 Convex Hull有点像，不过点数比较大，不能接受 o(n2) o(n^2)的算法。但是题目给定的是一个凸包，所以可以通过化简，在 o(n) o(n)的复杂度内计算出答案。首先，对于一个三角形ABC SABC=fA×fB+fB×fC+fC×fA(fi表示点i和原点组成的向量） S_{

暴力法解决最近对问题和凸包问题-实现可视化

目录最近对问题凸包问题最近对问题顾名思义就是采用蛮力法求出所有点之间的距离，然后进行比较找出第一个最近对，一个一个进行比较。大概思路就是如图（每个圈代表一个数对）第一个和其他四个比较第二个和其他三个比较 ....... 最后比较最小的代码图形化界面主要是easyx的graphics #include<iostream>#include <

POJ 1113 凸包模版题

题目：题目链接题目的意思就是让你求出凸包，然后在一凸包向外延伸L米。问此时的环的长度是多少？ #include <iostream>#include <cstdio>#include <string>#include <string.h>#include <map>#include <vector>#include <cstdlib>#include <cmath>#

POJ2007 凸包

题目：题目链接这道题目就是模版题，套用凸包的计算模版就行了 #include <iostream>#include <cstdlib>#include <cstring>#include <cstdio>#include <cmath>#include <algorithm>using namespace std;#define maxn 55#define pi acos

用c++实现最近对问题、凸包问题

5.5.1 最近对问题【问题】最近对问题(nearest points problem)要求在包含n个点的集合中找出距离最近的两个点。严格地讲，距离最近的点对可能多于一对，简单起见，只找出其中的一对即可。应用实例在空中交通控制问题中，若将飞机作为空间中移动的一个点来处理，则具有最大碰撞危险的两架飞机，就是这个空间中最接近的一对点。这类问题是计算几何中研究的基本问题之一。【想法】简单起见

CDQ分治维护凸包优化dp 【NOI2007】货币兑换cash bzoj1492

题目描述：小 Y 最近在一家金券交易所工作。该金券交易所只发行交易两种金券：A 纪念券（以下简称 A 券）和 B 纪念券（以下简称 B 券）。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动，两种金券都有自己当时的价值，即每一单位金券当天可以兑换的人民币数目。我们记录第 K 天中 A 券和 B 券的价值分别为 AK 和 BK （元/单位金