用c++实现最近对问题、凸包问题

本文主要是介绍用c++实现最近对问题、凸包问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

5.5.1 最近对问题

【问题】最近对问题(nearest points problem)要求在包含n个点的集合中找出距离最近的两个点。严格地讲，距离最近的点对可能多于一对，简单起见，只找出其中的一对即可。

应用实例
在空中交通控制问题中，若将飞机作为空间中移动的一个点来处理，则具有最大碰撞危险的两架飞机，就是这个空间中最接近的一对点。这类问题是计算几何中研究的基本问题之一。

【想法】 简单起见，只考虑二维的情况，假设所讨论的点以标准笛卡儿坐标形式给出，两个点pi=(xi,yi)和pj=(xj，yj)之间的距离是欧几里得(Euclidean distance)距离：

【算法】 蛮力法求解最近对问题的过程是显而易见的：分别计算每一对点之间的距离，然后找出距离最小的那一对。为了避免对同一对点计算两次距离，可以只考虑iくj 的点对(pi，pj)。在求欧几里得距离时，可以免去求平方根操作，因为如果被开方的数越小，则它的平方根也越小。
【算法实现】 设数组x[n]和y[n]存储n个点的坐标，函数 ClosestPoints 的形参index1 和 index2 以传引用形式接收最近点对的下标，假设最大距离不超过1000,程序如下。

#include <iostream>
using namespace std;

int ClosestPoints(int x[ ], int y[ ], int n, int &index1, int &index2)
{
int i, j, d, minDist = 1000;
for (i = 0; i < n - 1; i++)
for (j = i + 1; j < n; j++) //只考虑i＜j的点对
{
d = (x[i]-x[j])* (x[i]-x[j]) + (y[i]-y[j])* (y[i]-y[j]);
if (d < minDist)
{
minDist = d;
index1 = i; index2 = j;
}
}
return minDist;
}

int main( )
{
    int x[] = {1, 3, 5, 1};
    int y[] = {1, 2, 4, 2};
    int index1, index2;
    int minDist = ClosestPoints(x, y, 5, index1, index2);
    cout << "最接近的点对的距离为: " << minDist << endl;
    cout << "点对的索引为: " << index1 << " " << index2 << endl;
    return 0;
}

【算法分析】 算法 ClosestPoints的基本语句是计算两个点的欧几里得距离，主要操作是求平方，执行次数为
 

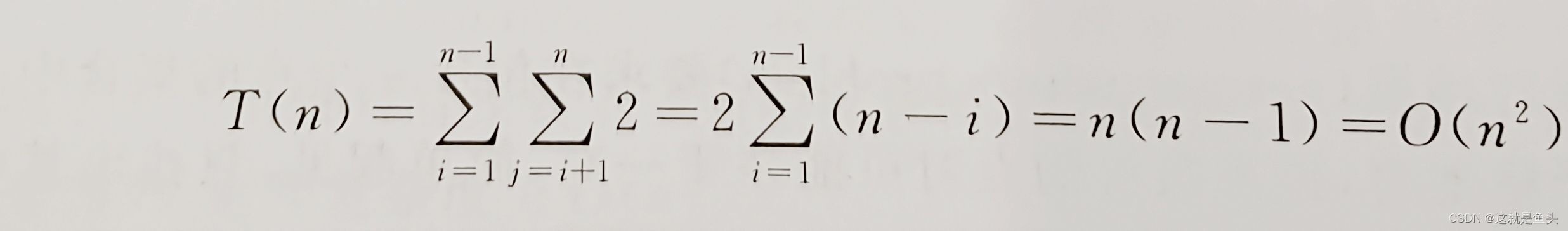
5.5.2  凸包 问题

定义5.1         对于平面上若干个点构成的有限集合，如果以集合中任意两点P和Q力端点的线段上的点都属于该集合，则称该集合是凸集合(convex set)。
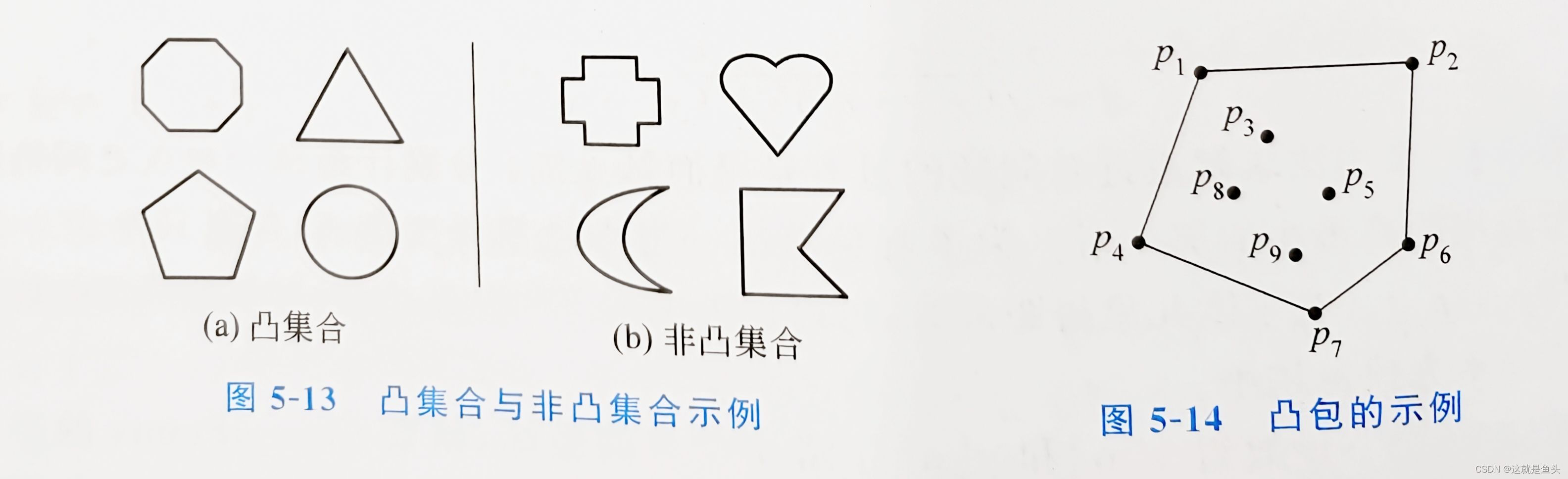
                     显然，任意凸多边形都是凸集合，图5-13给出了一些凸集合和非凸集合的例子。
定义5.2         一个点集S 的凸包(convex hull)是包含 S的最小凸集合，其中，最小是指S的凸包一定是所有包含S的凸集合的子集。
                     对于平面上几个点的集合S, 它的凸包就是包含所有这些点（或者在内部，或者在边
界上的最小凸多边形，最小凸多边形上的点称为凸包的极点(extreme dot)。图5-14给出了一个凸包的例子，其中，凸包的极点是p1、p2、p6、p7、p4。

应用 实 例
基于眼睛粗定位是将人脸区域送入分类器进行判别的人脸检测方法，该方法能够正确检测0°~360°旋转人脸图像，适用于非监视环境下的人脸检测。眼睛粗定位方法是一种基于彩色图像的定位方法，首先将皮肤部分提取出来，然后使用凸包填充算法，将大多数皮肤部分填充为凸包的形状，这样，就可以肯定在填充后的这些区域中，必定含有眼睛部分。

【问题】 凸包问题(convex hull problem)要求为平面上具有n个点的集合S构造最小凸多边形。
【想法】 设经过集合S中两个点(xi，yi)和(xj,yj)的线段是lij.如果该集合中的其他点都位于线段lij的同一侧（假定不存在三点同线的情况），则线段lij是该集合凸包边界的一部分。在平面上，经过两个点(xi，yi)和(xj，yj)的直线由下面的方程定义：
Ax+By+C=0 （其中，A=yi-y,j B=xj-xi, c=xiyj-xjyi)                (5-3)
        这条直线把平面分成两个半平面：其中一个半平面中的点都满足Az+By+C>0,另一个半平面中的点都满足Ac+By+C<o.
【算法】 可以基于上述原理设计一个简单但缺乏效率的算法：对于点集S中每一对顶点构成的线段，依次检验其余点是否位于这条线段的同一边。由于线段构成了凸包的边界，则满足条件的所有线段就构成了该凸包的边界。为了避免重复检验同一点对构成的线段，只考虑i<j的点对(pi,pj)。
【算法实现】 设数组x[n]和y[n]存储几个点的坐标，数组 px[n]和 py[n]存储所有极点的坐标，变量 signl 和 sign2 表示两个半平面，函数 BulgePack的返回值是极点的个数。程序如下。
 

#include <iostream>
using namespace std;

int BulgePack(int x[ ], int y[ ], int n, int px[ ], int py[ ])
{
int i, j, k, sign1, sign2;
int A, B, C, index = 0;
for (i = 0; i < n-1; i++)
for (j = i+1; j < n; j++)
{
sign1 = 0; sign2 = 0; //初始化sign1和sign2
A = y[i] - y[j]; B = x[j] - x[i]; C = x[i] * y[j] -x[j] * y[i];
for (k = 0; k < n; k++)
{
if (k != i && k != j)
{
if (A * x[k] + B * y[k] + C > 0) sign1 = 1;
else sign2 = 1;
if (sign1 == sign2) break; //两个半平面均有点
}
}
if (k == n) //点i和j是极点
{
px[index] = x[i]; py[index++] = y[i];
px[index] = x[j]; py[index++] = y[j];
}
}
return index;
}

int main( )
{
    int i, n = 5, x[5] = {1, 1, 2, 2, 3}, y[5] = {1, 2, 3, 4, 5};
    int px[5], py[5], num;

    num = BulgePack(x, y, n, px, py);
    cout << "极点有" << num << endl;

    for (i = 0; i < num; i = i + 2) {
        cout << "(" << px[i] << ", " << py[i] << ")" << endl;
    }

    return 0;
}
 

【算法分析】  所有不同的点组成了n(n-1)/2条线段，对每条线段都要计算所有点在表达式Ax+By+C中的符号，所以，算法的时间复杂度是O(n^3)。

这篇关于用c++实现最近对问题、凸包问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---