本文主要是介绍【Notes_2】现代图形学入门——Shading、光照模型、重心坐标、图形渲染管线、纹理映射,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
跟着闫令琪老师的课程学习,总结自己学习到的知识点
课程网址GAMES101
B站课程地址GAMES101
课程资料百度网盘【提取码:0000】
光栅化
着色(Shading)
在图形学中,着色的定义可以为:对物体(模型)应用某种材质。
主要是通过光照以及着色点参数进行表现。
在我们感知观察中,光线可以分为:高光、漫反射、环境光。

下面介绍一种简单的模型,对各种光照模型进行研究。
Bling-Phong Reflection Model
Phong反射模型
下图是光线照射到着色点上的示意图,为了便于分析,我们假设光线是从着色点方向发出。

Diffuse Reflection(漫反射)
漫反射: 当Phong模型表面是粗糙材质时,光照射到着色点时,会发生均匀反射,并且反射的光线的光强都相同。

那么每个入射的光线实际上照射到着色点的光强该怎么算。看下面的模型,首先光线与法线 n n n的夹角 θ \theta θ有关, cos ( θ ) = l ⃗ ⋅ n ⃗ \cos(\theta)=\vec{l}\cdot \vec{n} cos(θ)=l⋅n, ( l ⃗ 、 n ⃗ ) (\vec{l} 、\vec{n}) (l、n)为单位向量。

其次,图中中心为一个点光源,光线均匀的向周围发射,可以想象光源发射出来的能量其实是一定的,那么在任意两个圈上接受到的能量一定相等。而离圆心越远,圆的面积越大,单位面积所接受能量也就越弱。半径 r r r上的一点接收的能量为 I r 2 \frac{I}{r^2} r2I.

所以Diffuse Reflection可以用下面的式子表示

可以看出光强 L d L_d Ld与着色点表面参数 k d k_d kd、入射角 m a x ( 0 , n ⃗ ⋅ l ⃗ ) max(0,\vec{n} \cdot \vec{l}) max(0,n⋅l)、入射时的光强 I r 2 \frac{I}{r^2} r2I有关。
[Notes]: 入射角 m a x ( 0 , n ⃗ ⋅ l ⃗ ) max(0,\vec{n} \cdot \vec{l}) max(0,n⋅l) 最小为0。
下图反应了着色点的表面参数对Diffuse Reflection的影响。

Specular HighLight(高光)
高光发生的反射实际上是镜面反射,所以反射光线的范围很小。所以想要表示Specular Trem,需要表示反射光线与视点观测线之间的远近。
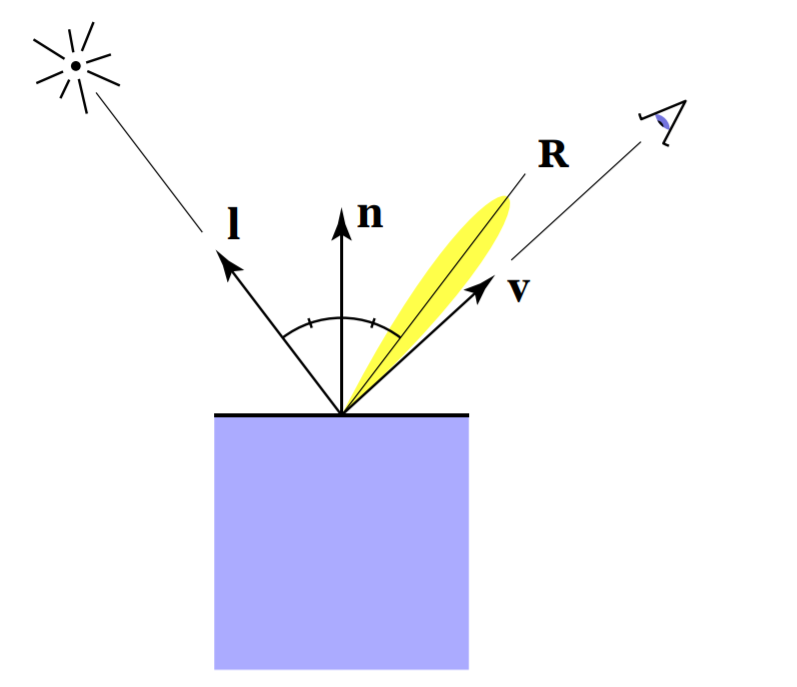
表示反射光线与视点观测线之间远近我们可以转化为求法线 n ⃗ \vec{n} n与半程向量 h ⃗ \vec{h} h之间的距离的远近。Specture Term也可以表示如下,仔细与Diffuse Term比较发现,Specture Term的相邻角是 m a x ( 0 , cos α ) p max(0,\cos \alpha)^p max(0,cosα)p,多了个指数。原因【图2】,镜面反射的范围通常小,所以增加指数,这样,可以很好模拟镜面反射范围小。



Ambient Term
环境光比较特殊、只有着色点表面因素的影响。

Blinn-Phong Reflection Model Term
基于以上三个式子,Bling-Phong模型的光照模型就可以表述出来了。

着色频率
前面我们知道了局部光照模型等式,但想要计算整个模型的光照模型,还需要知道每个模型上着色点的分布,引出了着色频率的概念。着色频率分为以下三种:Flat Shading、Gouraud Shading、Phong Shading,分别对应着三角形面着色、三角形顶点着色、每个点着色,以下是三种着色频率的效果。

Flat Shading(Shading each triangle)
在每个三角形的面上着色,对应着Flat Shading。每个三角形面的面法线只有一个,所以可以利用光照模型等式直接进行计算。这种着色效果是一个三角形面里的颜色一样,所以着色效果不平滑。

Gouraud Shading(Shading each vertex)
对每个三角形的顶点进行着色、对每个三角形面中间的颜色进性插值。Gouraud Shading着色有两个主要问题:
1 顶点着色时的法线怎么计算
2 怎样对三角形进行插值
顶点法线
1 最好的方法是对顶点的外接圆,然后找到对应点外接圆的法线即可。

2 平均每个顶点相接的面法线。
N v = ∑ i N i ∣ ∣ ∑ i N i ∣ ∣ N_v=\frac{\sum_i N_i}{||\sum_i N_i||} Nv=∣∣∑iNi∣∣∑iNi

插值
在讲插值之前首先要明白重心坐标。对三角形面内任意一点一定会有 α 、 β 、 γ \alpha、\beta、\gamma α、β、γ满足以下等式:
( x , y ) = α A + β B + γ C α + β + γ = 1 (x,y)=\alpha A+\beta B+\gamma C \\ \alpha+\beta+\gamma=1 (x,y)=αA+βB+γCα+β+γ=1

在三角形内部, α 、 β 、 γ \alpha 、\beta、\gamma α、β、γ为非负数,这可以作为判断点是否在三角形的依据。求解 α 、 β 、 γ \alpha 、\beta、\gamma α、β、γ就简单多了,
1 把三角形坐标带入上述公式,求解。
2 通过以下公式进行求解


3 通过以下公式进行求解

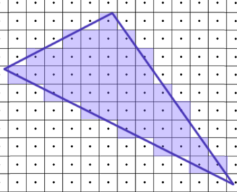
对已经得到 α 、 β 、 γ \alpha 、\beta、\gamma α、β、γ的重心坐标,满足以下性质:每个重心坐标的某个属性,都可以通过以下公式求解出来。下图是对重心坐标的颜色进行插值。

图形渲染管线主要是将场景中的3D物体通过管线转变为屏幕上的2D图像。主要包括两个功能:一是将物体的3D坐标转变为屏幕空间的2D坐标,二是为屏幕每个像素点进行着色。渲染管线的一般流程:顶点数据的输入、顶点着色器、曲面细分过程、几何着色器、图元组装、图元组装、裁剪剔除、光栅化、片段着色器以及混合测试。
渲染管线的一个特点就是每个阶段都会把前一个阶段的输出作为该阶段的输入。例如,片段着色器会将光栅化后的片段(以及片段的数据块)作为输入进行光照计算。除了图元组装和光栅化几个阶段是由硬件自动完成之外,管线的其他阶段管线都是可编程/可配置的。其中顶点着色器、曲面细分相关着色器、几何着色器和片段着色器是可编程的阶段,而混合测试是可高度配置的阶段。管线的可编程/可配置是渲染管理的另一个特点。因为早期的渲染管线采用的是立即渲染模式(Immediate mode,也就是固定渲染管线),不允许开发人员改变GPU渲染的方式,而核心渲染默认(Core-profile mode)允许开发人员定制化GPU的渲染方式。
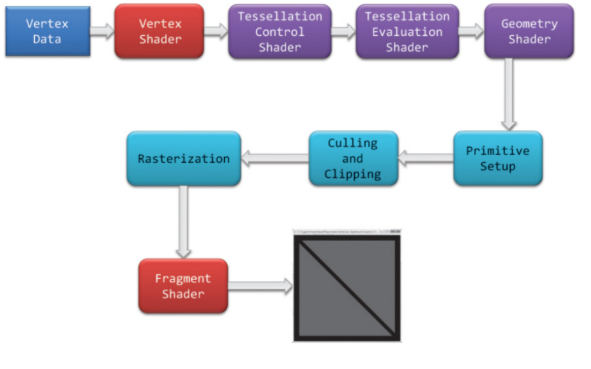
顶点数据: 顶点数据用来为后面的顶点着色器等阶段提供处理的数据。是渲染管线的数据主要来源。送入到渲染管线的数据包括顶点坐标、纹理坐标、顶点法线和顶点颜色等顶点属性。 为了让OpenGL明白顶点数据构成的是什么图元,我们需要在绘制指令中传递相对应的图元信息。常见的图元包括:点(GL_POINTS)、线(GL_LINES)、线条(GL_LINE_STRIP)、三角面(GL_TRIANGLES)。
顶点着色器: 顶点着色器主要功能是进行坐标变换。将输入的局部坐标变换到世界坐标、观察坐标和裁剪坐标。虽然我们也会在顶点着色器进行光照计算(称作高洛德着色),然后经过光栅化插值得到各个片段的颜色,但由于这种方法得到的光照比较不自然,所以一般在片段着色器进行光照计算。
曲面细分: 曲面细分是利用镶嵌化处理技术对三角面进行细分,以此来增加物体表面的三角面的数量,是渲染管线一个可选的阶段。它由外壳着色器(Hull Shader)、镶嵌器(Tessellator)和域着色器(Domain Shader)构成,其中外壳着色器和域着色器是可编程的,而镶嵌器是有硬件管理的。我们可以借助曲面细分的技术实现细节层次(Level-of-Detail)的机制,使得离摄像机越近的物体具有更加丰富的细节,而远离摄像机的物体具有较少的细节。
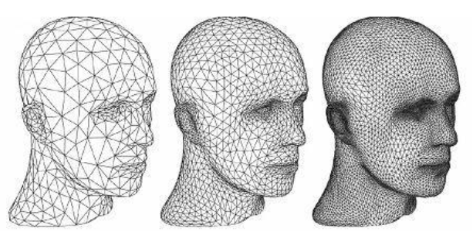
几何着色器: 几何着色器也是渲染管线一个可选的阶段。我们知道,顶点着色器的输入是单个顶点(以及属性), 输出的是经过变换后的顶点。与顶点着色器不同,几何着色器的输入是完整的图元(比如,点),输出可以是一个或多个其他的图元(比如,三角面),或者不输出任何的图元。几何着色器的拿手好戏就是将输入的点或线扩展成多边形。下图展示了几何着色器如何将点扩展成多边形。
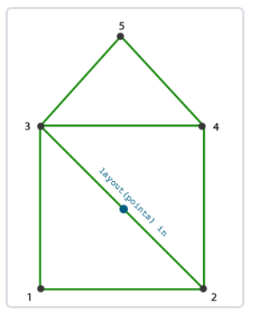
图元组装: 图元组装将输入的顶点组装成指定的图元。图元组装阶段会进行裁剪和背面剔除相关的优化,以减少进入光栅化的图元的数量,加速渲染过程。在光栅化之前,还会进行屏幕映射的操作:透视除法和视口变换。
关于透视除法和视口变换到底属于流水线的那个阶段并没有一个权威的说法,某些资料将这两个操作归入到图元组装阶段,某些资料将它归入到光栅化过程,但对我们理解整个渲染管线并没有太大的影响,我们只需要知道在光栅化前需要进行屏幕映射就可以了,所以我们这里将屏幕映射放到了图元组装过程。这两个操作主要是硬件实现,不同厂商会有不同的设计。
光栅化: 经过图元组装以及屏幕映射阶段后,我们将物体坐标变换到了窗口坐标。光栅化是个离散化的过程,将3D连续的物体转化为离散屏幕像素点的过程。包括三角形组装和三角形遍历两个阶段。光栅化会确定图元所覆盖的片段,利用顶点属性插值得到片段的属性信息,然后送到片段着色器进行颜色计算,我们这里需要注意到片段是像素的候选者,只有通过后续的测试,片段才会成为最终显示的像素点。
片段着色器: 片段着色器在DirectX中也成为像素着色器(Pixel Shader)。片段着色器用来决定屏幕上像素的最终颜色。在这个阶段会进行光照计算以及阴影处理,是渲染管线高级效果产生的地方。主要的操作有:Z-buffer可视性、着色(Shading)、纹理映射(Texture mapping)。
测试混合阶段: 管线的最后一个阶段是测试混合阶段。测试包括裁切测试、Alpha测试、模板测试和深度测试。没有经过测试的片段会被丢弃,不需要进行混合阶段;经过测试的片段会进入混合阶段。Alpha混合可以根据片段的alpha值进行混合,用来产生半透明的效果。Alpha表示的是物体的不透明度,因此alpha=1表示完全不透明,alpha=0表示完全透明。测试混合阶段虽然不是可编程阶段,但是我们可以通过OpenGL或DirectX提供的接口进行配置,定制混合和测试的方式。
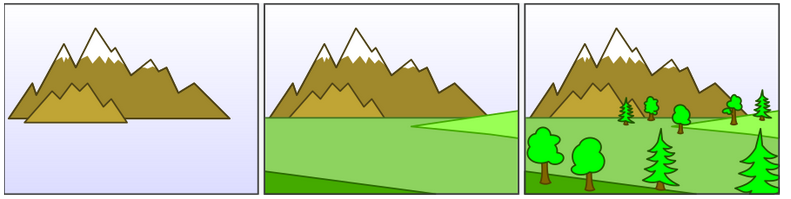
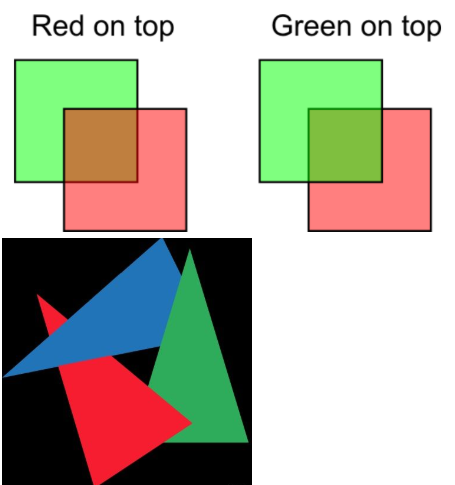
值得注意的是,半透明物体的绘制需要遵循画家算法(painter Algorithm)由远及近进行绘制,因为半透明的混合跟物体的顺序有严格的对应关系。从下面两张图我们可以看到,先绘制红色还是先绘制绿色对最终颜色的有这很大的影响。所以,绘制半透明物体之前,我们需要按照距离远近对场景中的物体进行严格排序,然而这是一个非常棘手的问题。比如,我们如何排序下面几个三角形呢?所以当进行半透明物体渲染时,一般会使用顺序无关的半透明渲染技术(Order-independent transparency,OIT)。
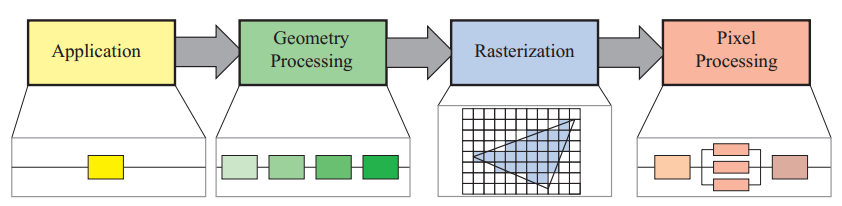
渲染管线并非严格这样划分,不同的教材会有不同的划分方法。《Real Time Rendering》一书将渲染管线划分为以下四个阶段:应用程序阶段(Application)、几何处理阶段(Geometry Processing)、光栅化(Rasterization)和像素处理阶段(Pixel Processing)。应用阶段通常是在CPU端进行处理,包括碰撞检测、动画物理模拟以及视椎体剔除等任务,这个阶段会将数据送到渲染管线中;几何处理阶段主要执行顶点着色器、投影变换、裁剪和屏幕映射的功能;光栅化阶段和我们上面讨论的差不多,都是将图元离散化片段的过程;像素处理阶段包括像素着色和混合的功能。我们可以发现,虽然管线的划分粒度不一样,但是每个阶段的具体功能其实是差不多的,原理也是一样的,并没有太大的差异。
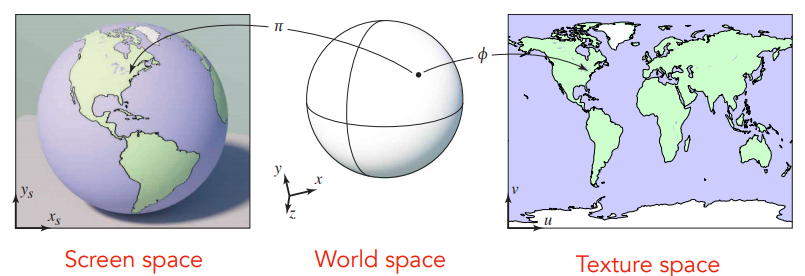
纹理坐标
每个3D模型上的三角形如果对应到2D平面,就可以用纹理坐标 ( u , v ) (u,v) (u,v) 表示,坐标分为在[0,1]内

示例:纹理坐标 ( u , v ) (u,v) (u,v)可以通过重心坐标插值的方法得到。


纹理放大(Texture Magnification)

当纹理图片过小,就会出现多个像素点仍然对应一个 ( u , v ) (u,v) (u,v)坐标,并将该 ( u , v ) (u,v) (u,v)坐标下颜色信息复制给该像素点,这样形成的图片边界过渡就会非常不自然,形成一个个的小格子。如下图:

解决上述问题的方法就是双线性插值。
双线性插值(Bilinear Interpolation)
双线性插值就是在充分利用屏幕空间 f ( x , y ) f(x,y) f(x,y)的四周的值,求出一个方向(例如 s s s)上点 f ( x , y ) f(x,y) f(x,y)的值,利用同样的方法,直至求出所有方向的值。利用这种方法得到的结果不会出现一个个小格子的现象。


纹理缩小(Texture Minification)
引用博客计算机图形学系列笔记
当纹理图过大,近处会出现锯齿、远处出现摩尔纹的现象。
根据引入的博客进行解释:
1 根据近大远小,远处的一张完整的贴图可能在屏幕空间中仅仅是几个像素的大小,那么必然屏幕空间的一个像素对应了纹理贴图上的一片范围的点,这其实就是纹理过大所导致的,直观来说想用一个点采样的结果代替纹理空间一片范围的颜色信息,必然会导致严重失真!(从信号的角度来说就是,采样频率过低无法还原信号原貌
2 换一种想法,考虑离相机很远的一个三角形面,假设该三角形面真正在纹理贴图上对应的一片区域有10个像素点。但是由于透视的关系,距离很远的三角形面投影到近平面时可能只有1个或2个像素点的大小(远远小于10个像素的原来大小),那么这1个或2个像素采样texture的结果就要代表原来这个三角形面10个像素点的颜色信息,自然会导致失真!

解决方法就是MipMap技术。
MipMap
MipMap就是将纹理进行分层,像素应用不同层次纹理。


但是这里D值算出来是一个连续值,并不是一个整数,有两种对应的方法:
1 四舍五入取得最近的那个level D
2 利用D值在 向下和向上取整的两个不同level进行三线性插值
通过MipMap分层之后,进行纹理映射得到的效果,边界过渡生硬,可以通过三线性插值的方法解决

三线性插值
拓展双线性插值,分别对D层级、D+1层级的MipMap进行双线性插值、在根据实际得到的D值进行线性插值,得到最终的结果。




纹理应用
纹理对着色有影响,不仅仅是对颜色的影响,还可以改变法线的高度来影响着色。
Bump Mapping
纹理通过定义法线高度,可以实现改变模型来增加模型的表面细节。


接下来是求纹理表面的法线。
In Flatland

in 3D

Displacement mapping
Displacement Mapping比Bump Mapping的更先进,Bump的边缘部分会出现Artifacts。

几何
几何表示
隐式表示
不给出点的坐标,给数学表达式
优点 可以很容易找到点与几何之间的关系

缺点 找某特定的点很难
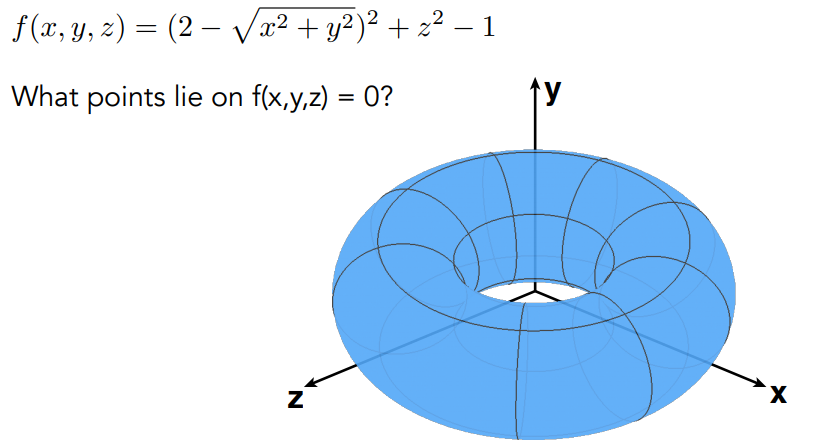
更多的隐式表示方法
Constructive Solid Geometry 、Distance Functions 、Level Set Methods 、Fractals
显示表示
直接给出点或者参数映射
优点 找某一点很容易
缺点 判断点与几何之间的关系很困难
更多的显式表示方法
Triangle meshes 、Bezier surfaces 、Subdivision surfaces 、NURBS 、Point clouds。
其中需要强调的一点在图形学中,显示存储在文件的格式是wavefront object file。
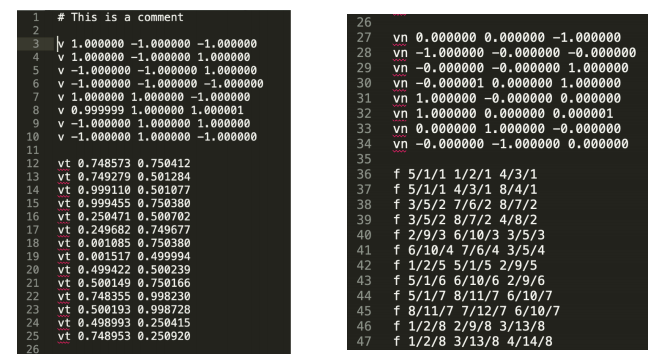
其中, v : v: v:顶点、 v n : v_n: vn:法线、 v t : v_t: vt:纹理坐标、 f f f参数详解:(顶点坐标 纹理坐标 法线坐标)
光线追踪
动画和模拟
这篇关于【Notes_2】现代图形学入门——Shading、光照模型、重心坐标、图形渲染管线、纹理映射的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








