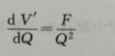运筹学专题
清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 及 通过使用文件或者套节字来识别进程的fuser命令
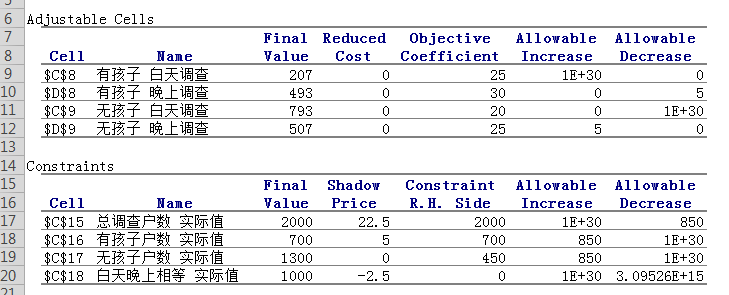
一、清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 最近又接触了一些线性求解的问题,以前主要都是在高中数学里接触到,都是使用笔算,最后通过一些函数式得出最小或者最大值,最近的研究生学业上接触到了一个Excel solver分析工具,对这种线性求最优解的问题感觉使用起来真是得心应手。在使用这个工具前,EXCEL里需要先装上solver工具,装起来很也简单,网上
2024年中国运筹学会运筹竞赛(数据驱动赛道)报名通知
竞赛组织 主办单位:中国运筹学会(国家一级学会) 承办单位:中国科学技术大学 支持单位:杉数科技、海康威视、中国科学技术大学管理学院、《运筹学学报》杂志 竞赛内容 本次竞赛(本科生组)由竞赛专家委员会根据企业实际数据命题,参赛作品为包括背景介绍、模型建立与求解、算法设计与实现、结果分析、改进思路等方面的论文和必要附件(如算法代码、计算结果、中间结果的图表等)。 竞赛流程 报名
自考《运筹学》之宏观理解
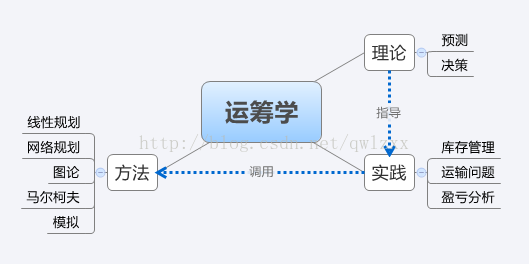
运筹学是现代管理学的一门重要专业基础课。它是20世纪30年代初发展起来的一门新兴学科,其主要目的是在决策时为管理人员提供科学依据,是实现有效管理、正确决策和现代化管理的重要方法之一。该学科是一应用数学和形式科学的跨领域研究,利用统计学、数学模型和算法等方法,去寻找复杂问题中的最佳或近似最佳的解答。运筹学经常用于解决现实生活中的复杂问题,特别是改善或优化现有系统的效率。 研究运筹学
运筹帷幄之中,决胜千里之外——运筹学1-3章
运筹学第一章主要讲了运筹学的原理,产生的背景,以及分类方法,应用运筹学进行决策的过程。 感觉很接近运筹学实际应用的一句话是:作为运筹学应用者,接受管理部门的要求,去收集和阐明数据,建立和试验数学模型,预言未来作业,然后制定方案,并推荐给经理部门。 感觉跟诸葛亮和吴用做的事很相似。他们观察天文地理,时政格局,人文心理,然后预测未来发展
运筹学_3.运输问题(特殊的线性规划)
目录 前言3.1 平衡运输问题中初始基可行解确定运输问题平衡运输与非平衡运输平衡运输问题的数学模型单纯形法解决平衡运输问题,初始可行基的确认 3.2 平衡运输问题的最优解判别求检验数表上作业法 3.3 产销不平衡的运输问题运输问题中产大于销的问题运输问题中产小于销的问题 前言 运输问题是一类具有特殊结构的线性规划问题,运输问题由于约束方程组的特殊性,存在着比单纯形法更简单的特殊
【软考高项】四十六、项目管理科学计算之运筹学
1、线性规划问题 解题思路: 先把文字转化成图表 最快方式应该是把第一题的4个答案直接代入计算,很快得知X=2时利润最大。 A=0时,利润=5*6=30 A=2时,利润=2*2+5*6=34 A=4时,利润=4*2+3*5=23 A=6时,利润=4*2(因为甲的资源上限,A最多4个) 2、运输问题 伏格尔方法主旨:最大差额处,优先按最小运价进行调运 计算方法:先计
服务运营 | 精选:用药难?用药贵?运筹学与统计学视角下的药物研发与管理
作者设计了一个多阶段博弈论模型来针对罕见病的不同补贴方案,分析政府、联盟、制药商和患者之间的相互作用。 制药商补贴为 α C \alpha C αC,其中 C C C是研发成本, α ∈ [ 0 , 1 ) \alpha \in [0,1) α∈[0,1)是政府总成本的比例。患者补贴为 β p i \beta p_i βpi,其中 p i p_i pi是药品每单位售价, β \beta β是
【2024年5月备考新增】《软考真题分章练习(含答案解析) - 17 管理科学-运筹学基础 (1)》
管理科学-运筹学基础 1、小李作为项目经理需要从以下四个项目方案中选择项目,已知项目周期均为 2 年且期初投资额都是30.000 元,折现均为 10%。项目情况如下: 方案 A:第一年现金流为 14,000 元,第二年现金流 19,000 元 方案 B:第一年现金流为 23,000 元,第二年现金流 20,000 元 方案 C:第一年现金流为 18,000 元,第二年现金流 24,000 元 方案
运筹学基础(六)列生成算法(Column generation)
文章目录 前言从Cutting stock problem说起常规建模Column generation reformulation 列生成法核心思想相关概念Master Problem (MP)Linear Master Problem (LMP)Restricted Linear Master Problem (RLMP)subproblem(核能预警,非常重要) 算法流程图CG求解cu
运筹学_1.1.4 线性规划问题-解的概念
1.1.4 线性规划问题-解的概念 一、可行解与最优解二、基的概念三、基变量、基向量;非基变量、非基向量;基解、基可行解;四、最优解与可行解、基可行解的关系五、用例题(枚举法)巩固基解、基可行解、最优解三个概念1、例12、例2 六、解之间的关系归纳 一、可行解与最优解 可行解:满足所由约束条件的解【全部可行解的集合称为可行域】 最优解:使目标函数最大的可行解 因此最优解包含
运筹学_1.2线性规划问题的几何意义
1.2线性规划问题的几何意义 一、凸集的基本概念二、由线性规划问题的几何意义、定理得出的几点结论三、引出单纯形法的解题步骤 一、凸集的基本概念 通俗来说,一个图形上任意两个点的连线上的点全部存在于这个图形中 二、由线性规划问题的几何意义、定理得出的几点结论 三、引出单纯形法的解题步骤
【天池直播】同济梁教授运筹学系列直播二--列生成
同济梁教授运筹学系列直播二:列生成。 对列生成想要了解以及有任何疑问的同学,请在帖子【点击跳转】留言,梁教授会统一解答哦~ 直播主题:运筹学系列直播--列生成 直播时间:11月2日 20:00 直播链接:点击直播 直播嘉宾: 梁哲 天池昵称梁哲 同济大学同济大学管理科学与工程教授博导,天池航空AI大赛冠军团队“同济经管组合优化”导师。 曾为北京大学工学院特聘研究员。 直播内容 1.列生成简介
【天池直播】同济梁教授运筹学系列直播三--列生成2:万变不离其宗,强大的并行机排程!...
鸠摩智靠着小无相功的内功,用少林72绝学打败了少林寺的大和尚,并行机排程,即列生成中的小无相功。 本次直播,我们且看并行机在人员排班,医疗卫生,车辆运输,航空排程,生产运作等方面的应用。 对并行机排程想要了解以及有任何疑问的同学,请在技术圈帖子留言,梁教授会统一解答哦~ 直播主题:列生成2--万变不离其宗,强大的并行机排程! 直播时间:11月9日 20:00 直播链接:点击查看 直播嘉宾:
【天池直播】同济教授分享应用算法优化航空运营(第一场运筹学领域直播)...
本周邀请同济大学教授、航空AI大赛冠军团队导师带来应用算法优化航空运营的分享。 梁老师将从时间维度上简要介绍航空公司运营过程中的规划步骤和关键流程,并以 “机组排班问题”和“飞机维护路由问题”两个核心业务难题为重点详细展开。 从问题的定义,到目标、约束剖析,再到模型的具体形式,以及大规模线性规划问题求解的列生成方法。 直播主题:应用算法优化航空运营 直播时间:10月26日 20:00 直播链接:
运筹学代码基础(python)
运筹学基础 python基础操作字典 线性规划问题求解例题建模问题的矩阵表示决策变量取值受限 0 和 1最小生成树问题最小路径问题 python 基础操作 加减法和输出0 p1 = 987654321p2 = 123456789print(p1 +
【0基础运筹学】【SCIP论文】【3.1.2 Feasibility Pump(可行性泵)】Primal Heuristics for Mixed Integer Programs
目录 相关教程相关文献前言从一个例子出发:预备知识Feasibility Pump(可行性泵)Feasibility Pump流程图流程细节The Objective Feasibility PumpDealing with Cycles伪代码 Feasibility Pump(可行性泵)是一种启发式算法寻找MIP问题可行解的算法。 相关教程 【0基础运筹学】【SCIP论文
运筹学知识点总结 (十)
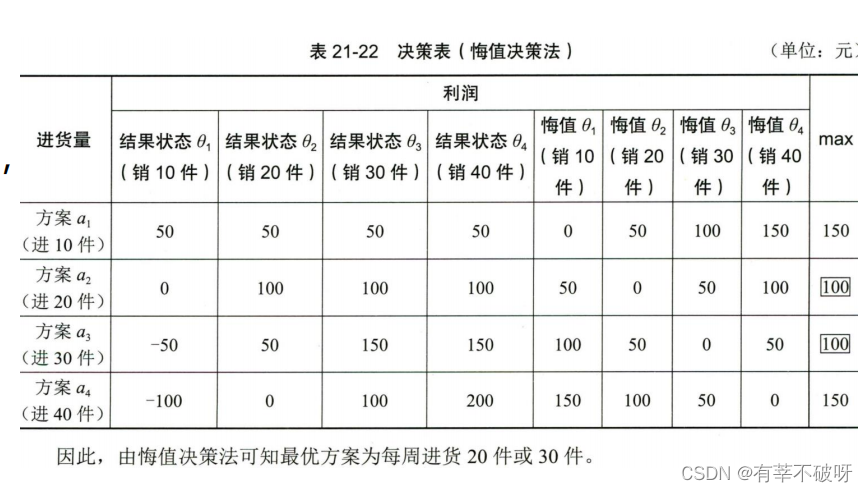
运筹学知识点全套 目录 第十章 盈亏分析模型一、盈亏分析二、盈亏平衡分析是一种管理决策工具三、盈亏平衡问题中的成品与销售分析四、产品成本结构五、工业产品的成本费用六、产品销售结构七、线性盈亏分析模型八、 盈亏平衡图九、非线性盈亏平衡图十、非线性盈亏分析模型的应用十一、边际收益、边际收益率和生产能力百分率的计算 第十章 盈亏分析模型 一、盈亏分析 盈亏分析就是对企业产品的成
运筹学经典问题(一):指派问题
问题描述 有 N N N个任务,需要 N N N个人去完成,每个人完成不同工作的效率不同(或者资源、收益等等),需要怎么分配使得整体的效率最高(成本最低等等)呢?这就是经典的指派问题啦! 数学建模 我们首先做以下定义: I I I: 人的集合; J J J: 任务的集合; c i j c_{ij} cij: 把任务 j j j分配给 i i i的成本; x i j x_{ij}
体系化学习运筹学基础算法的实践和总结
文章目录 引言目标设计目标实践文章汇总经验总结一则预告 引言 眨眼间已经12月了,眼看着2023年马上要过完了。 女朋友最近总说,工作以后感觉时间过的好快。事实上,我也是这么认为的。年纪越大,越会担心35岁危机的降临。所以,人还是应该持续学习和进步的。具体来说,就是在工作时间之外,每年都能有一些关于自身的成长。 23年初,我给自身成长设置了一系列目标,其中之一就是体系化。这里
运筹学-使用python建模基本操作
运筹学中的python基本操作 运筹学库的基本介绍MIP 库的使用networkx 库的使用 运筹学 所谓运筹学(Operation Research) 就是用数学方法研究各种系统最优化问题的学科,为决策者提供科学决策的依据,求解系统最优化问题,制定合理运用人力,物力,财力的方案。 库的基本介绍 对于python来说,相较于其他语言,最大的优势之一就是数据巨大的库,众多开发者
运筹学-使用python建模基本操作
运筹学中的python基本操作 运筹学库的基本介绍MIP 库的使用networkx 库的使用 运筹学 所谓运筹学(Operation Research) 就是用数学方法研究各种系统最优化问题的学科,为决策者提供科学决策的依据,求解系统最优化问题,制定合理运用人力,物力,财力的方案。 库的基本介绍 对于python来说,相较于其他语言,最大的优势之一就是数据巨大的库,众多开发者
【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析 最大流问题 最大流问题的数学规划模型为: max v = f 12 + f 13 { f 12 + f 13 − f 57 − f 67 = 0 f 13 + f 23 = f 34 + f 35 . . . 0 ≤ f i j ≤ c i j \max v=f_{12}+f_{13}\\ \begin{cases} f_{12}+f_{13}-f_{57}-f_{67}
【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析 最大流问题 最大流问题的数学规划模型为: max v = f 12 + f 13 { f 12 + f 13 − f 57 − f 67 = 0 f 13 + f 23 = f 34 + f 35 . . . 0 ≤ f i j ≤ c i j \max v=f_{12}+f_{13}\\ \begin{cases} f_{12}+f_{13}-f_{57}-f_{67}