本文主要是介绍体系化学习运筹学基础算法的实践和总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 引言
- 目标设计
- 目标实践
- 文章汇总
- 经验总结
- 一则预告
引言
眨眼间已经12月了,眼看着2023年马上要过完了。
女朋友最近总说,工作以后感觉时间过的好快。事实上,我也是这么认为的。年纪越大,越会担心35岁危机的降临。所以,人还是应该持续学习和进步的。具体来说,就是在工作时间之外,每年都能有一些关于自身的成长。
23年初,我给自身成长设置了一系列目标,其中之一就是体系化。这里的体系化,主要包含两项,第一项是运筹学基础算法的体系化,第二项是机器学习算法的体系化。到了年尾,应该为一年的工作做一个总结了。
本文将着重分享今年在第一项(运筹学基础算法)上的实践和总结,后续文章将再聊另外一个内容。
正文见下。
目标设计
科学体系化的方式,私以为应该是参考各种专业书的目录,然后结合自己的认知,做个性化设计。 举个例子,《运筹学》(清华大学出版社)这本书是直接从线性规划问题开始的,但是求解线性规划问题的单纯形法,对我来说已经比较复杂,不能算入门了。
下图是我今年初给自己安排的体系化学习目标。
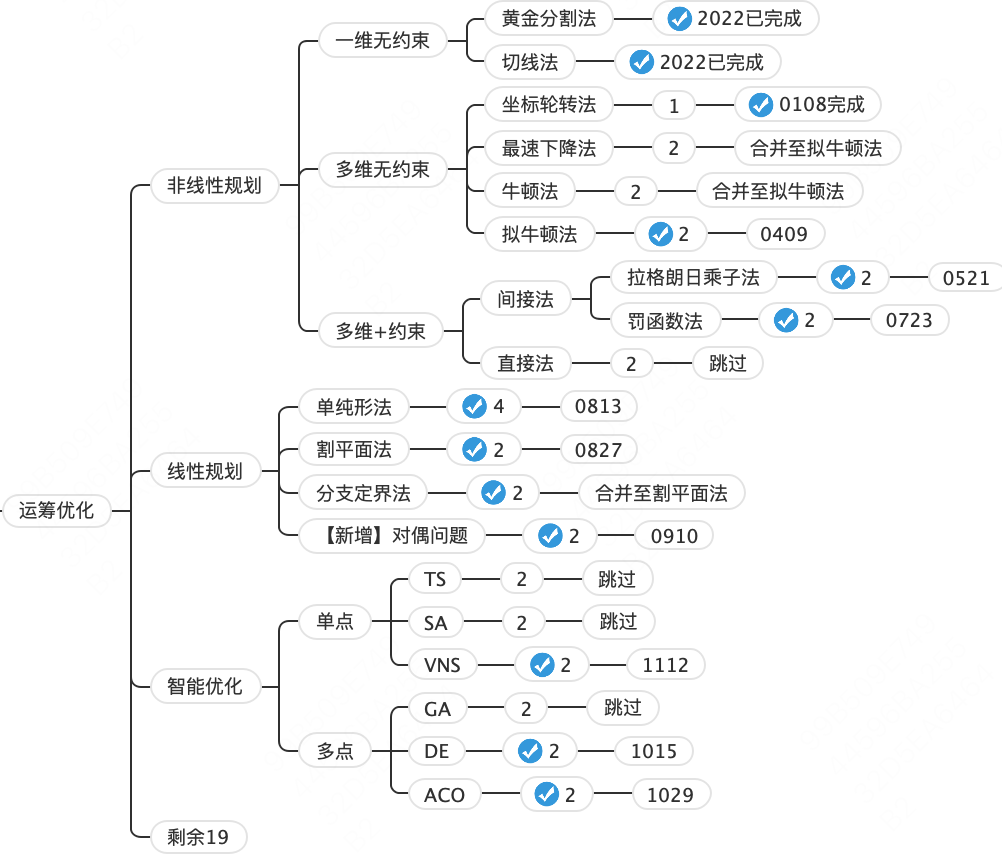
我认为,学习过程要从简单到复杂。而最简单的运筹问题,应该是一维无约束问题,在此基础上再提升问题维度和增加不同类型的约束条件。这些内容,在我年初的体系化学习目标中被归类为非线性规划模块。现在想来,“非线性规划”这个模块的标题并不是很准确,不过也没想到更好的,就继续用这个吧。
理解了以上普适性较好的基本算法体系后,我觉得才适合来研究线性/整数规划这一类在实际业务中被广泛研究的问题和对应的求解算法。
除了非线性规划、线性规划和整数规划外,还要学习智能优化算法的主要原因,是我觉得这些算法的改进尝试中,针对迭代方向和迭代步长的设计很有艺术感,虽然缺乏严格的数学证明,但在实践中已经被证明为非常有效的手段。
目标实践
对于大部分算法,我给自己预设的目标是两周学习完,这样最终评估下来能有19周的剩余时间。
从剩余时间来说,我给自己安排的计划,算是比较宽松的。我一直觉得,工作和学习应该是为生活服务的,如果发生了冲突,那幸福的生活体验应该放在第一位。所以我从一开始就没想着给自己太大的压力,如果觉得有些累了,偷懒玩游戏、看视频,甚至只是无聊发呆,也不会有太大的负罪感。
实际也是如此——从完成度来看,我最后一篇文章是VNS,11月12号完成的,距离12月31号只剩6周,也就是说我在年中的时候荒废了13周左右的时间。
我对算法学习完成的定义是,写一篇与算法内容对应的文章,里面至少应该包含2个模块:
第一个是用自己的逻辑描述清楚算法原理。我对自己的要求是,让算法小白都能看懂内容,如果未来真的有机会教书育人,这应该是我宝贵的财富了;
第二个是自己编写代码实现算法全过程。我对自己的要求是,分别用Python和Java编程实现,以验证自己是否真的理解了算法原理,同时提升代码能力。
从实际完成度来看,每一个算法相关的文章都算是及格了。对算法原理的描述,我还是比较满意的,特别是收到小伙伴们的暖心评论和留言时,都会备受鼓舞。在代码实现方面,并没有达到预期,开始阶段一些简单的算法还能用Python和Java分别实现,到了中后期算法复杂度提升后就有些力不从心了。在认清现实后,我去掉了使用Java实现算法过程的目标。针对特别复杂的算法,甚至都不要求自己手写了。
看,我就是这么容易和自己和解。
文章汇总
本节汇总了近一年运筹学基础算法的相关文章和链接,并按照此前的目标设计进行了分类。
| 分类 | 文章和链接 |
|---|---|
| 非线性规划-黄金分割法 | Python和Java代码实现:黄金分割法求解一维最优化问题 |
| 非线性规划-切线法 | Python和Java代码实现:切线法求解一维最优化问题 |
| 非线性规划-坐标轮转法 | Python代码实现:坐标轮换法求解多维最优化问题 |
| 非线性规划-梯度类算法 | 梯度类算法原理:最速下降法、牛顿法和拟牛顿法 拟牛顿法:python代码实现 |
| 非线性规划-间接法 | 求解包含约束的最优化问题:拉格朗日乘子法和KKT条件 |
| 非线规划-直接法 | 求解包含约束的最优化问题:罚函数法 |
| 线性规划-单纯形法 | 线性规划和单纯形法-原理篇 线性规划模型-工程应用篇 |
| 线性规划-整数规划 | 求解整数规划问题的割平面法和分支定界法 稍微憋个招,聊聊为什么不能止步于会调求解器 |
| 线性规划-对偶问题 | 线性规划对偶问题:理论推导和实际应用 |
| 智能优化-DE | 差分进化算法,依旧强势 |
| 智能优化-ACO | 蚁群算法求包含34个国内城市的TSP,和最优解相差没那么大 |
| 智能优化-ALNS | 着实不错的自适应大邻域搜索算法ALNS |
经验总结
关于这一年来对于运筹算法的学习和感悟,总结如下:
首先,这些算法在运筹学中算是基础内容。通过对这些知识点的学习和总结,我自身受益匪浅,在一定程度上弥补了我因为非科班出身导致基础知识储备的欠缺。不过这只是一个开始,随着认知的提升,可能会发现未知的内容也越来越多,后续还有很多内容需要去慢慢探索。
其次,在学习上我是偏应用导向的。当初选择运筹学作为自己未来长期从事的行业,主要是觉得把这些算法策略应用到实际场景中能带来极大的成就感,所以我不太会执着于理论上的推导,在学习知识时,会优先选择工业实践中最常用的运筹算法,并辅以部分基础的算法原理,以知其然并知其所以然。
最后,这些知识点的串联方式是基于我目前的认知。图中的分类仅依赖于我当前体系化学习的实践路径,算不上权威,可以作为大家构建自己知识体系的参考。
一则预告
明年运筹优化领域的文章主题,偷偷预告一下,大概率是随机优化和鲁棒优化,即,模型输入存在不确定性情况下的最优决策。
具体的学习路径,我还没思考清楚——当然了,即使已经想清楚了,我也不会直接公开出来,大概率会类似于这样,等明年年底总结吧!
最后的最后,愿大家都能持之以恒地做一件件小事,慢慢努力,惊艳众人。
这篇关于体系化学习运筹学基础算法的实践和总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





