本文主要是介绍【0基础运筹学】【SCIP论文】【3.1.2 Feasibility Pump(可行性泵)】Primal Heuristics for Mixed Integer Programs,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 相关教程
- 相关文献
- 前言
- 从一个例子出发:
- 预备知识
- Feasibility Pump(可行性泵)
- Feasibility Pump
- 流程图
- 流程细节
- The Objective Feasibility Pump
- Dealing with Cycles
- 伪代码
Feasibility Pump(可行性泵)是一种启发式算法寻找MIP问题可行解的算法。
相关教程
- 【0基础运筹学】【SCIP论文】【3.1.1 Some Simple Divers】Primal Heuristics for Mixed Integer Programs
- 【0基础运筹学】【SCIP论文】【3.2.1 RENS】Primal Heuristics for Mixed Integer Programs
- 【0基础运筹学】【SCIP论文】【3.2.2 Some Other Rounding Methods】Primal Heuristics for Mixed Integer Programs
相关文献
- [1] Achterberg T . Constraint Integer Programming. Springer Berlin Heidelberg, 2007.
- [2] Berthold T . Primal Heuristics for Mixed Integer Programs[J]. master’s thesis technische universität, 2006.
- [3] Fischetti M , Glover F , Lodi A . The feasibility pump[J]. Mathematical Programming, 2005, 104(1):91-104.
前言
之前一直想跟大家分享一下【1】Achterberg T . Constraint Integer Programming. Springer Berlin Heidelberg, 2007.、【2】Berthold T . Primal Heuristics for Mixed Integer Programs[J]. master’s thesis technische universität, 2006.,这两篇SCIP官方文献,也全网搜了许多文档、视频、论文等。大部分教程抽象程度较高,需要具备大量的基础知识才能看明白,于是写一篇尽可能0基础上手的分享,希望能帮到也在从事相关行业的你。
2023新年FLAG:SCIP两篇文章分享更新计划完成!!!——@小猪快跑
从一个例子出发:
我们先看一个简单的MIP问题:
max 7 x + y \max{7x+y} max7x+y
s . t . s.t. s.t.
x ≤ 2 x \leq 2 x≤2
y ≤ 2 y \leq 2 y≤2
3 x − y ≤ 4 3x-y \leq 4 3x−y≤4
4 x + y ≤ 9 4x+y \leq 9 4x+y≤9
x + 5 y ≤ 11 x+5y \leq 11 x+5y≤11
x , y ∈ N x,y\in\mathbb{N} x,y∈N
一般情况来说,求解MIP问题的松弛解(LP)会比原问题快很多,但松弛解通常是不可行的,这时候我们希望通过松弛解得到原问题的可行解。
原问题的LP问题:
max 7 x + y \max{7x+y} max7x+y
s . t . s.t. s.t.
x ≤ 2 x \leq 2 x≤2
y ≤ 2 y \leq 2 y≤2
6 x − y ≤ 8 6x-y \leq 8 6x−y≤8
5 x + 2 y ≤ 11 5x+2y \leq 11 5x+2y≤11
2 x + 9 y ≤ 20 2x+9y \leq 20 2x+9y≤20
x , y ∈ R , x , y ≥ 0 x,y\in\mathbb{R},x,y\geq 0 x,y∈R,x,y≥0
求解得到:
x = 1.86 x = 1.86 x=1.86
y = 1.57 y = 1.57 y=1.57
我们有一个大胆的猜测,就是原问题(MIP)的解和LP的解距离非常接近。其实这也是非常合理的猜测,如下图所示,我们只要向下平移 7 x + y = 12.65 7x+y=12.65 7x+y=12.65,然后和可行域有整数解的交点就是MIP的可行解了,而越接近 7 x + y = 12.65 7x+y=12.65 7x+y=12.65,目标 max 7 x + y \max{7x+y} max7x+y 值越大。
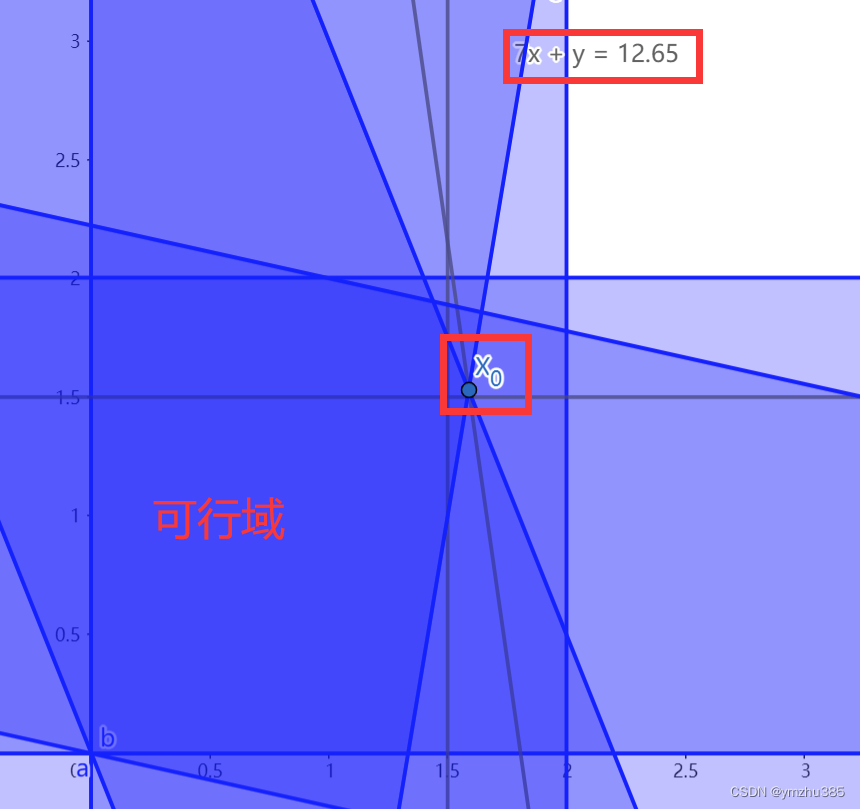
我们最直接的思想肯定是把点 X 0 ( x = 1.86 , y = 1.57 ) X_0(x=1.86, y=1.57) X0(x=1.86,y=1.57) 圆整(四舍五入): X 1 ( x = 2 , y = 2 ) X_1(x=2, y=2) X1(x=2,y=2) ,这时候点 X 1 X_1 X1离最优解很近,并且他是一个整数解(可能不可行)。我们从下图中发现点 X 1 ( x = 2 , y = 2 ) X_1(x=2, y=2) X1(x=2,y=2)并不在可行域。
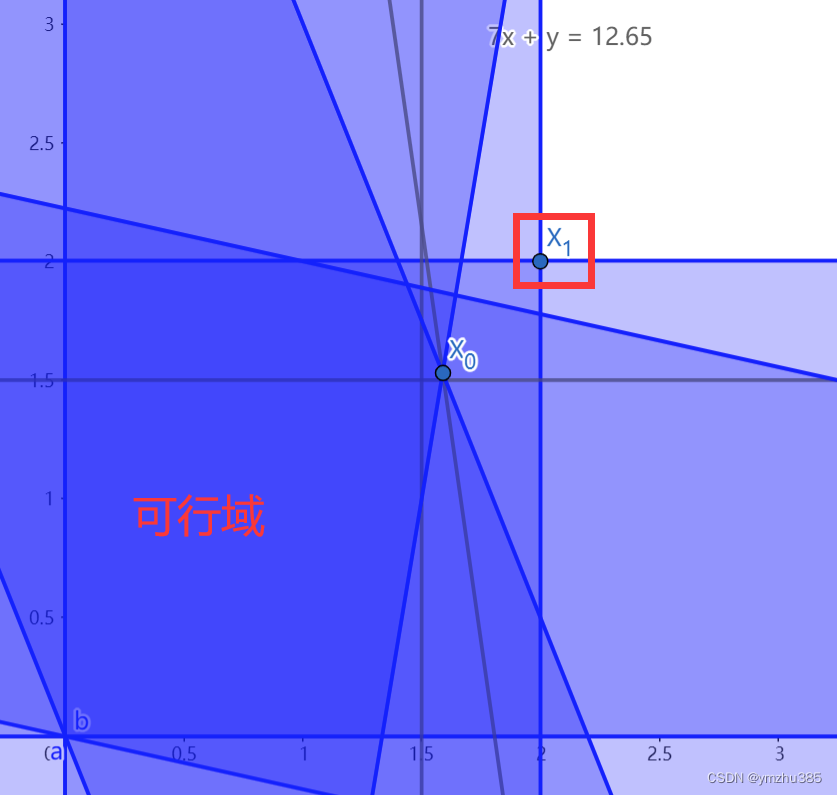
但我们能够发现如果在点 X 1 X_1 X1的 L 1 L_1 L1-范数距离<=1有 X 1 , l e f t , X 1 , r i g h t , X 1 , u p , X 1 , d o w n X_{1,left}, X_{1,right},X_{1,up},X_{1,down} X1,left,X1,right,X1,up,X1,down四个整数点,其中 X 1 , l e f t X_{1,left} X1,left在可行域里。
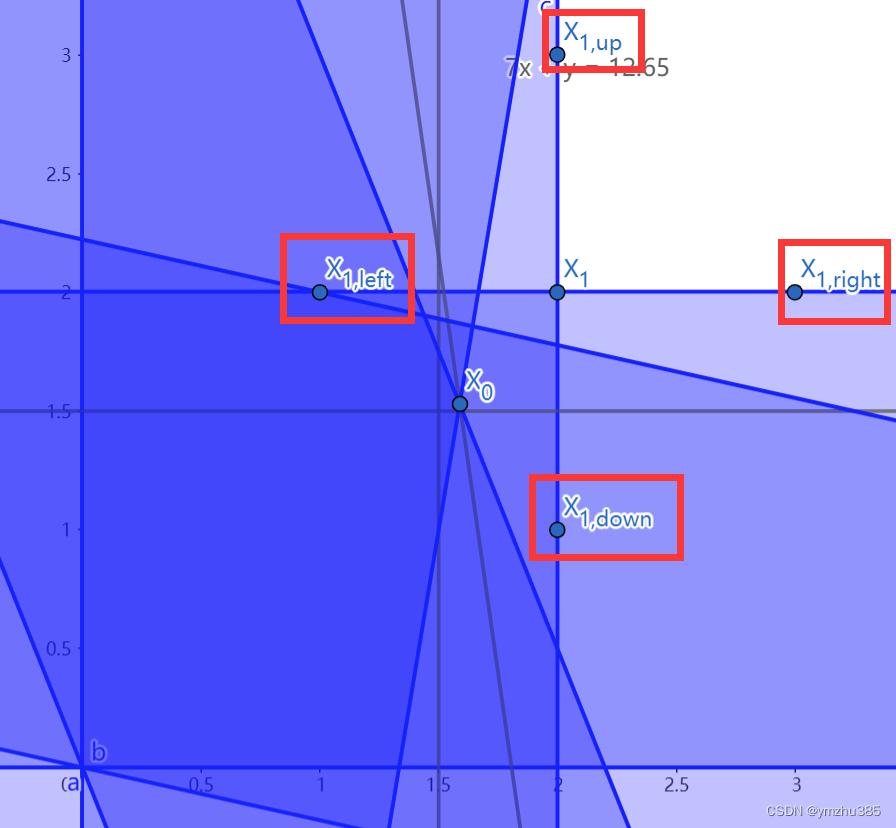
于是我们大胆的猜测,在点 X 1 X_1 X1的 L 1 L_1 L1-范数距离很小的时候找到的可行解离最优解距离也很近。也就是说其实我们想找一个点,这个点离 X 1 ( x = 2 , y = 2 ) X_1(x=2, y=2) X1(x=2,y=2)越接近越好,这个点还要在可行域内。于是我们有:
min ∣ 2 − x ∣ + ∣ 2 − y ∣ \min{\left|2-x\right|+\left|2-y\right|} min∣2−x∣+∣2−y∣
s . t . s.t. s.t.
x ≤ 2 x \leq 2 x≤2
y ≤ 2 y \leq 2 y≤2
6 x − y ≤ 8 6x-y \leq 8 6x−y≤8
5 x + 2 y ≤ 11 5x+2y \leq 11 5x+2y≤11
2 x + 9 y ≤ 20 2x+9y \leq 20 2x+9y≤20
x , y ∈ R , x , y ≥ 0 x,y\in\mathbb{R},x,y\geq 0 x,y∈R,x,y≥0
因为 x ≤ 2 x \leq 2 x≤2, y ≤ 2 y \leq 2 y≤2,所以目标 min ∣ 2 − x ∣ + ∣ 2 − y ∣ \min{\left|2-x\right|+\left|2-y\right|} min∣2−x∣+∣2−y∣可以把绝对值去掉。于是我们有:
min ( 2 − x ) + ( 2 − y ) \min{(2-x)+(2-y)} min(2−x)+(2−y)
s . t . s.t. s.t.
x ≤ 2 x \leq 2 x≤2
y ≤ 2 y \leq 2 y≤2
6 x − y ≤ 8 6x-y \leq 8 6x−y≤8
5 x + 2 y ≤ 11 5x+2y \leq 11 5x+2y≤11
2 x + 9 y ≤ 20 2x+9y \leq 20 2x+9y≤20
x , y ∈ R , x , y ≥ 0 x,y\in\mathbb{R},x,y\geq 0 x,y∈R,x,y≥0
求解得到:
x = 1.44 x = 1.44 x=1.44
y = 1.90 y = 1.90 y=1.90
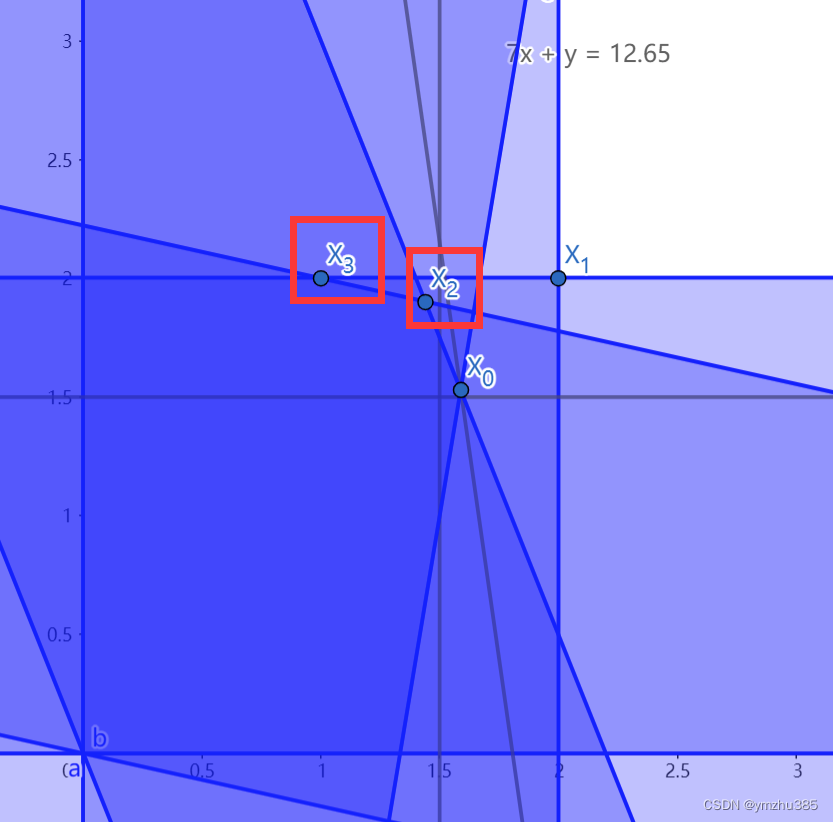
于是我们在图中标注 X 2 ( x = 1.44 , y = 1.90 ) X_2(x=1.44, y=1.90) X2(x=1.44,y=1.90),重复之前的步骤,直接圆整LP的解得到 X 3 ( x = 1 , y = 2 ) X_3(x=1, y=2) X3(x=1,y=2),我们很容易验证 X 3 X_3 X3在可行域内,他就是原问题(MIP)的一个可行解(在这个问题中刚好也是最优解)。
预备知识
定义: R ^ : = R ∪ { ± ∞ } \hat{\mathbb{R}}:=\mathbb{R}\cup\{\pm\infty\} R^:=R∪{±∞}
定义1.1 m , n ∈ R , A ∈ R m × n , b ∈ R m , c ∈ R n , l , u ∈ R ^ , I ⊆ N = { 1 , ⋅ ⋅ ⋅ , n } m,\,n\,\in\,\mathbb{R},\ A\in\ \mathbb{R}^{m\times n},\ b\in\ \mathbb{R}^{m},\ c\in\mathbb{R}^{n},\ l,\,u\in\hat{\mathbb{R}}\ ,{I}\subseteq{\cal N}=\{1,\cdot\cdot\cdot,n\} m,n∈R, A∈ Rm×n, b∈ Rm, c∈Rn, l,u∈R^ ,I⊆N={1,⋅⋅⋅,n}
min c T x s u c h t h a t A x ≤ b l ≤ x ≤ u x j ∈ Z f o r a l l j ∈ I \begin{array}{r l l} {\min}&{{}c^Tx}\\ {such\ that}&{{}A x\leq b}\\ &{l\leq x\leq u}\\ &x_{j}\in\mathbb{Z} &for\ all\ j\in I \end{array} minsuch thatcTxAx≤bl≤x≤uxj∈Zfor all j∈I 我们称这是一个混合整数规划(mixed integer program (MIP))。
定义1.2 给定MIP如定义1.1所示,我们称:
a l i n e a r p r o g r a m ( L P ) i f I = ∅ a n i n t e g e r p r o g r a m ( I P ) i f I = N a b i n a r y p r o g r a m ( B P ) i f B = I = N , a n d a m i x e d b i n a r y p r o g r a m ( M B P ) i f B = I . \begin{array}{r l l} {a\ \mathrm{linear\ program\ (LP)}}&{if}&{I=\emptyset}\\ {an\ \mathrm{integer\ program\ (IP)}}&{if}&{I=N}\\ {a\ \mathrm{binary\ program\ (BP)}}&{if}&{B = I = N, and}\\ {a\ \mathrm{mixed\ binary\ program\ (MBP)}}&{if}&{B = I.} \end{array} a linear program (LP)an integer program (IP)a binary program (BP)a mixed binary program (MBP)ififififI=∅I=NB=I=N,andB=I. 其中 B : = { j ∈ I ∣ l j = 0 , u j = 1 } B:=\{j\in I\mid l_{j}=0,u_{j}=1\} B:={j∈I∣lj=0,uj=1}
定义1.3 给定MIP如定义1.1所示,我们称:
L P − f e a s i b l e f o r ( 1.1 ) i f A x ^ ≤ b a n d l ≤ x ^ ≤ u , i n t e g e r f e a s i b l e f o r ( 1.1 ) i f x ^ j ∈ Z f o r a l l j ∈ I , a f e a s i b l e s o l u t i o n f o r ( 1.1 ) i f x ^ i s L P − f e a s i b l e a n d i n t e g e r f e a s i b l e , a n d a n o p t i m a l s o l u t i o n f o r ( 1.1 ) i f x ^ i s a f e a s i b l e s o l u t i o n a n d c T x ^ ≤ c T x f o r a l l o t h e r f e a s i b l e s o l u t i o n s x . \begin{array}{r l l} {\mathrm{LP-feasible}\ for\ \mathrm{(1.1)}}&{if}&{A{\hat{x}}\leq b\ and\ l\leq\hat{x}\leq u,}\\ {\mathrm{integer\ feasible }\ for\ \mathrm{(1.1)}}&{if}&{\hat{x}_{j}\in\mathbb{Z}\quad f o r\ a l l\;j\in I,}\\ {a\ \mathrm{feasible\ solution }\ for\ \mathrm{(1.1)}}&{if}&{\hat{x}\ is\ LP-feasible\ and\ integer\ feasible,\ and}\\ {an\ \mathrm{optimal\ solution }\ for\ \mathrm{(1.1)}}&{if}&{\hat{x}\ is\ a\ feasible\ solution\ and\ c^{T}{\hat{x}}\leq c^{T}x}\\ &&{for\ all\ other\ feasible\ solutions\ x.} \end{array} LP−feasible for (1.1)integer feasible for (1.1)a feasible solution for (1.1)an optimal solution for (1.1)ififififAx^≤b and l≤x^≤u,x^j∈Zfor allj∈I,x^ is LP−feasible and integer feasible, andx^ is a feasible solution and cTx^≤cTxfor all other feasible solutions x. 如果给定一个MIP,通过省略整数约束( x j ∈ Z f o r a l l j ∈ I x_{j}\in\mathbb{Z}{\mathrm{~for~all~}}j\in I xj∈Z for all j∈I)而产生的LP被称为MIP的LP松弛(LP-relaxation)。 P ( A , b , l , u ) : = { x ∈ R n ∣ A x ≤ b , l ≤ x ≤ u } P(A,b,l,u):=\{x\in\mathbb{R}^{n}\mid A x\leq b,l\leq x\leq u\} P(A,b,l,u):={x∈Rn∣Ax≤b,l≤x≤u}被称为MIP的LP多面体(LP-polyhedron)。
Feasibility Pump(可行性泵)
Feasibility Pump
定义3.2 S ⊆ N S\subseteq N S⊆N, x ∈ R n x\in\mathbb{R}^{n} x∈Rn
[ x ] j S : = { ⌊ x j + 0.5 ⌋ i f j ∈ S x j i f j ∉ S . [x]_{j}^{S}:=\left\{\begin{array}{l l}{{\left\lfloor x_{j}+0.5\right\rfloor}}&{{i f\;j\in S}}\\ {{x_{j}}}&{{i f\;j\notin S.}}\end{array}\right. [x]jS:={⌊xj+0.5⌋xjifj∈Sifj∈/S. 【友情提示】: [ x ] j S [x]_{j}^{S} [x]jS 相当于指标 j j j在 S S S里的话, x j x_j xj进行四舍五入。
Δ S ( x , y ) : = ∑ j ∈ S ∣ x j − y j ∣ {\Delta}^{S}(x,y):=\sum_{j\in S}|x_{j}-y_{j}| ΔS(x,y):=j∈S∑∣xj−yj∣ 【友情提示】: Δ S ( x , y ) {\Delta}^{S}(x,y) ΔS(x,y) 相当于指标 j j j在 S S S里的话, x x x和 y y y的 L 1 − d i s t a n c e L_{1}-d i s t a n c e L1−distance。
f S ( x ) : = ∑ j ∈ S f ( x j ) w i t h f ( x j ) : = ∣ x j − ⌊ x j + 0.5 ⌋ ∣ f^{S}(x):=\sum_{j\in S}f(x_{j}) \quad with \quad f(x_{j}):=|x_{j}-\lfloor x_{j}+0.5\rfloor| fS(x):=j∈S∑f(xj)withf(xj):=∣xj−⌊xj+0.5⌋∣ 【友情提示】: f S ( x ) f^{S}(x) fS(x)相当于对于指标 j j j在 S S S里的话,向量 x ∈ R n x\in\mathbb{R}^{n} x∈Rn的分数部分(离最近整数的距离)绝对值求和。
流程图

流程细节
- 求原问题的LP松弛解,记为 x ˉ \bar{x} xˉ。
- x ˉ \bar{x} xˉ中本应是整数变量但可能存在小数的情况,于是我们四舍五入: x ~ ← [ x ˉ ] S {\tilde{x}} \leftarrow [{\bar{x}}]^{S} x~←[xˉ]S
- 这时候 x ~ {\tilde{x}} x~可能不可行,根据上面举得例子我们猜测:原问题(MIP)的解和LP的解距离非常接近。于是乎我们跟上面例子一样,希望找一个点 x ˉ \bar{x} xˉ满足: x ~ {\tilde{x}} x~ 的 L 1 − L_1- L1− 范数距离很小时候的LP可行解。
x ˉ : = arg min { Δ S ( x , x ~ ) ∣ x ∈ P ( A , b , l , u ) } \bar{x}:=\argmin\{\Delta^{S}(x,\tilde{x})\mid x\in P(A,b,l,u)\} xˉ:=argmin{ΔS(x,x~)∣x∈P(A,b,l,u)} 也就是说,我们只需要求解如下LP问题:
min ∑ j ∈ S : x ~ j = l j ( x j − l j ) + ∑ j ∈ S : x ~ j = u j ( u j − x j ) + ∑ j ∈ S , l j < x ~ j < u j d j s u c h t h a t A x ≤ b x − x ~ ≤ d x ~ − x ≤ d l ≤ x ≤ u \min \sum_{j\in S:{\tilde{x}}_{j}=l_{j}}(x_{j}-l_{j}) + \sum_{j\in S:{\tilde{x}}_{j}=u_{j}}(u_{j}-x_{j}) + \sum_{j\in S,l_{j}\lt {\tilde{x}}_{j}\lt u_{j}}d_{j}\\ \begin{array}{l r} {\mathrm{such\ that}}&{A x\leq b}\\ &{x-\tilde{x}\leq d}\\ &{\tilde{x}-x\leq d}\\ &{l\leq x\leq u} \end{array} minj∈S:x~j=lj∑(xj−lj)+j∈S:x~j=uj∑(uj−xj)+j∈S,lj<x~j<uj∑djsuch thatAx≤bx−x~≤dx~−x≤dl≤x≤u 这里我们希望 x x x 和 x ~ \tilde{x} x~ 的 L 1 − L_1- L1− 范数距离小: ∣ x − x ~ ∣ ≤ d ⇔ { x − x ~ ≤ d x ~ − x ≤ d {|x-\tilde{x}|\leq d}\Leftrightarrow \left\{\begin{aligned} {x-\tilde{x}\leq d}\\ {\tilde{x}-x\leq d}\\ \end{aligned}\right. ∣x−x~∣≤d⇔{x−x~≤dx~−x≤d ,所以我们有了上面的约束。(注:如果 S = B S=B S=B,则不需要创建变量 d j d_j dj) - 重复步骤2和3,迭代直到 x ˉ = x ~ \bar{x}=\tilde{x} xˉ=x~ ,也就是得到一个MILP可行解。
Feasibility Pump算法思想主要利用了定义1.3:a feasible solution if x ^ \hat{x} x^ is LP-feasible and integer feasible 。LP-feasible通过求解松弛问题(LP)即可,integer feasible取整即可。从几何学的角度来看,FP(Feasibility Pump)产生了两个点 x ˉ \bar{x} xˉ 和 x ~ \tilde{x} x~ 的轨迹(希望是收敛的),它们以互补的方式满足部分的可行性,一个满足线性约束,另一个满足整数要求。该方法引导 x ˉ \bar{x} xˉ 走向可行性的一个重要特征:我们在每个pumping cycle(指的是步骤2和3)计算 x ˉ \bar{x} xˉ 与多面体P的 L 1 − L_1- L1− 范数距离 ( x , x ~ ) (x,\tilde{x}) (x,x~),而不是像MIP启发式方法中惯用的那样,对单个线性约束的违反程度进行加权组合(instead of taking a weighted combination of the degree of violation of the single linear constraints)(这句博主目前也不是特别理解)。这个距离可以解释为 x ˉ \bar{x} xˉ 和 ( x , x ~ ) (x,\tilde{x}) (x,x~) 的 “压力差”,我们试图通过将 x ˉ \bar{x} xˉ 的整体性 "泵入 " ( x , x ~ ) (x,\tilde{x}) (x,x~) 来减少这种压力——这就是方法名称的由来。FP可以被解释为一种产生四舍五入序列的算法,从而生成可行的MIP点。FP也可以被看作是修正的local branching策略。事实上,在每个pumping cycle,我们都有一个满足整数要求的(可能不可行)的解决方案 x ˉ \bar{x} xˉ,我们面临的问题是在一个小距离的邻域内找到一个可行的解决方案(如果存在的话),即只改变其变量的一个小子集。在 local branching 的背景下,这个子问题的模型是MIP: min { c T x : A x ≥ b , Δ S ( x , x ~ ) ≤ k } \min\{c^{T}x:A x\geq b,\ \Delta^{S}(x,\tilde{x})\leq k\} min{cTx:Ax≥b, ΔS(x,x~)≤k},其中 k k k 是一个合适的值。在FP背景下,相同的子问题通过一种宽松的方式建模就是步骤3中的模型,其中 "小距离 "的要求被转化为目标函数的条件。
The Objective Feasibility Pump
计算结果表明,Feasibility Pump在寻找MIP的可行解是非常成功的。不幸的是,解的质量有时是相当差的。这可以从这样的观察中得到解释:MIP的原始目标函数 c c c 只用到过一次,即当第一个LP可行点 x ˉ \bar{x} xˉ 被确定为LP-relaxation的最优解时。Achterberg和Berthold提供了一个修改版的Feasibility Pump,称为 Objective Feasibility Pump,它比原Feasibility Pump更多地考虑了目标函数。Objective Feasibility Pump在第一次迭代后并不完全忽略目标函数c,而是在每个迭代步骤中减少其影响。因此,它的运行时间越长,就越趋向于可行性,越趋向于最优性。如果不存在适当的原始目标函数,即 c = 0 c=0 c=0,我们将只使用Feasibility Pump的原始版本。为了避免一些技术上的困难,我们假设 c ≠ 0 c\neq0 c=0。这里我们考虑用 Δ S ( ⋅ , x ˉ ) \Delta^{S}(\cdot,{\bar{x}}) ΔS(⋅,xˉ) 和 c c c 的凸组合(convex combination)替换 Δ S ( ⋅ , x ˉ ) \Delta^{S}(\cdot,{\bar{x}}) ΔS(⋅,xˉ)。
定义3.3 L e t x ~ ∈ R n , S ⊆ N , c ∈ R n \ { 0 } , a n d α ∈ [ 0 , 1 ] . L e t\ \tilde{x}\in\mathbb{R}^{n},\ S\subseteq N,\ c\in\mathbb{R}^{n}\backslash\{0\},\ a n d\,\alpha\in[0,1]. Let x~∈Rn, S⊆N, c∈Rn\{0}, andα∈[0,1].
Δ α S ( x , x ~ ) : = ( 1 − α ) Δ S ( x , x ~ ) + α ∣ S ∣ ∥ c ∥ c T x \Delta_{\alpha}^{S}(x,\tilde{x}):=(1-\alpha)\Delta^{S}(x,\tilde{x})+\alpha\frac{\sqrt{|S|}}{\|c\|}c^{T}x ΔαS(x,x~):=(1−α)ΔS(x,x~)+α∥c∥∣S∣cTx 【友情提示】: ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣是Euclidean范数,即 ∣ ∣ x ∣ ∣ 2 = ∑ i x i 2 ||x||_{2}={\sqrt{\sum_{i}x_{i}^{2}}} ∣∣x∣∣2=∑ixi2。
【友情提示】: ∣ S ∣ \sqrt{|S|} ∣S∣ 是 Feasibility Pump 原始版本的Euclidean范数,这里我们把 Δ S ( ⋅ , x ˉ ) \Delta^{S}(\cdot,{\bar{x}}) ΔS(⋅,xˉ) 看成一种距离的定义,那么其Euclidean范数即
∣ S ∣ = ∑ j ∈ S : x ~ j = l j ( x j − l j ) 2 + ∑ j ∈ S : x ~ j = u j ( u j − x j ) 2 + ∑ j ∈ S , l j < x ~ j < u j d j 2 \sqrt{|S|}=\sqrt{\sum_{j\in S:{\tilde{x}}_{j}=l_{j}}(x_{j}-l_{j}) ^2+ \sum_{j\in S:{\tilde{x}}_{j}=u_{j}}(u_{j}-x_{j}) ^2+ \sum_{j\in S,l_{j}\lt {\tilde{x}}_{j}\lt u_{j}}d^2_{j}} ∣S∣=j∈S:x~j=lj∑(xj−lj)2+j∈S:x~j=uj∑(uj−xj)2+j∈S,lj<x~j<uj∑dj2。
【友情提示】: α t + 1 = φ α t , φ ∈ [ 0 , 1 ) , α 0 ∈ [ 0 , 1 ] . \alpha_{t+1}=\varphi\alpha_{t}, \varphi\in[0,1), \alpha_{0}\ \in\ [0,1]. αt+1=φαt,φ∈[0,1),α0 ∈ [0,1].
Dealing with Cycles
在Feasibility Pump的两个变体中都出现了一个主要问题:如果取整后的点 x ~ \tilde{x} x~,而这个点在之前的迭代中已经被访问过,那么该怎么办?处理这种方式的紧迫性在两个版本中都不一样。对于最初的Feasibility Pump来说,返回到一个已经被访问过的点意味着陷入一个循环。Feasibility Pump会找到完全相同的最接近的点 x ˉ \bar{x} xˉ,会像之前的迭代一样把它四舍五入到相同的整数可行点,因此,会一次又一次地得到整个点的序列。因此,Fischetti, Glover和Lodi建议进行重启操作。
重启会进行随机扰动,将最后一个LP可行解 x ˉ \bar{x} xˉ 的一些变量值随机地向上或向下移动,而不是像通常那样四舍五入。如果有一个长度为1的循环,这意味着你立即转回前一次迭代的舍入点 x ~ \tilde{x} x~,你将跳过随机选择,而只是把一定数量的比如说最小 T T T 个变量舍入到另一边。
Objective Feasibility Pump在不同的迭代步骤 t t t 和 t ′ t^′ t′ 中使用不同的参数 α t α_t αt 和 α t ′ α_{t^′} αt′。由于不同的目标函数 α t α_t αt 和 α t ′ α_{t^′} αt′,有可能到达一个新的LP可行点 x ˉ \bar{x} xˉ ,即使已经访问过 x ~ \tilde{x} x~,也不会遇到循环。这一事件的概率显然取决于两个函数 α t α_t αt 和 α t ′ α_{t^′} αt′的差异程度,而这本身又取决于 α t α_t αt 和 α t ′ α_{t^′} αt′的差异程度。只有在迭代 t ′ < t t^′<t t′<t 时已经访问过点 x ~ \tilde{x} x~,且 α t ′ − α t ≤ δ α \alpha_{t^{\prime}}-\alpha_{t}\leq\delta_{\alpha} αt′−αt≤δα,其中 δ α ∈ ( 0 , 1 ] \delta_{\alpha}\in(0,1] δα∈(0,1] 是一个固定的参数值,Objective Feasibility Pump才会在迭代 t t t 时执行重新启动。
伪代码

这篇关于【0基础运筹学】【SCIP论文】【3.1.2 Feasibility Pump(可行性泵)】Primal Heuristics for Mixed Integer Programs的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





