跳跃专题
2024.9.1 Python,跳跃游戏,贪心算法,回溯算法复原 IP 地址,关于回溯过程中列表的[:]以及copy问题再讨论
先祝各位C友们9月快乐,生活幸福。 1.跳跃游戏,贪心算法 昨天的三个代码我写到最后没时间去盘了,今天来盘一下,昨天我写的第一个代码从逻辑上就有问题,所以不停的报错不停的报错,我在报错的过程中不断地去加可能性,但是加一种可能就只解决一种问题,所以说明问题没有在根本上解决,所以我便在今天去看之前的代码有什么问题,我的代码如下: #错的class Solution:def jump(self,
Leetcode面试经典150题-45.跳跃游戏II
解法都在代码里,不懂就留言或者私信,这个题绝对比动态规划的解法强 class Solution {/**本题我们先不用动态规划了,因为从任何一个位置都可能跳到最后一个位置,用动态规划的成本太高了本题的解题思路:看看某个步数内最多能跳到多远,如果某步内能涵盖最后一个位置,那这个就是最小的步数 */public int jump(int[] nums) {/**你就在终点,跳啥啊 */if(num
Redis 跳跃表的实现
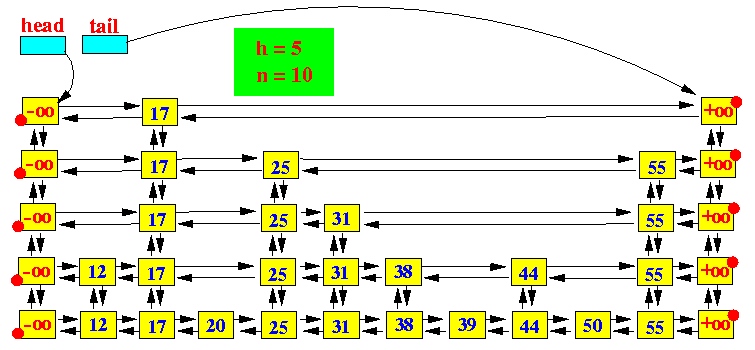
概述 跳跃表 SkipList 是一种有序数据结构,通过在每个节点中维持多个指向其它节点的指针,达到快速访问节点的目的 平均时间复杂度 O(logN),在大部分情况下,跳跃表的效率与平衡树相近,由于跳跃表实现的简易性,所以 Redis 使用跳表代替平衡树。 ZSET 存储元素,使用了 哈希表以及、SkipList 作为底层实现。 typedef struct zset {dict *dic
代码随想录Day 28|题目:122.买卖股票的最佳时机Ⅱ、55.跳跃游戏、45.跳跃游戏Ⅱ、1005.K次取反后最大化的数组和
提示:DDU,供自己复习使用。欢迎大家前来讨论~ 文章目录 题目题目一:122.买卖股票的最佳时机 II贪心算法:动态规划 题目二:55.跳跃游戏解题思路: 题目三: 45.跳跃游戏 II解题思路方法一方法二 题目四:1005.K次取反后最大化的数组和解题思路 总结 贪心算法继续刷题 题目 题目一:122.买卖股票的最佳时机 II 122. 买卖股票的最佳时机 II 贪心
算法训练第24天|122.买卖股票的最佳时机II|55. 跳跃游戏|45.跳跃游戏II|1005.K次取反后最大化的数组和
LeetCode 122.买卖股票的最佳时机II 题目链接:122.买卖股票的最佳时机II 题目讲解:代码随想录 func maxProfit(prices []int) int {var sum intfor i := 1; i < len(prices); i++{if prices[i] - prices[i - 1] > 0{sum += prices[i] - prices[i
力扣题解(跳跃游戏II)
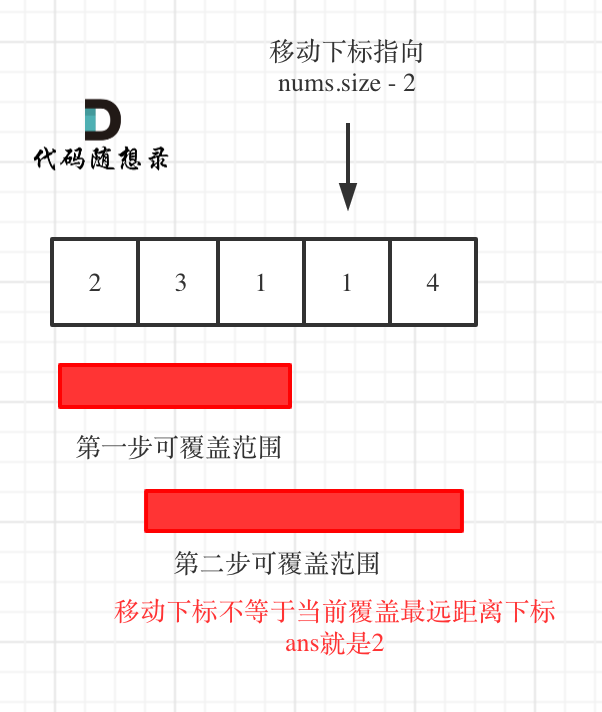
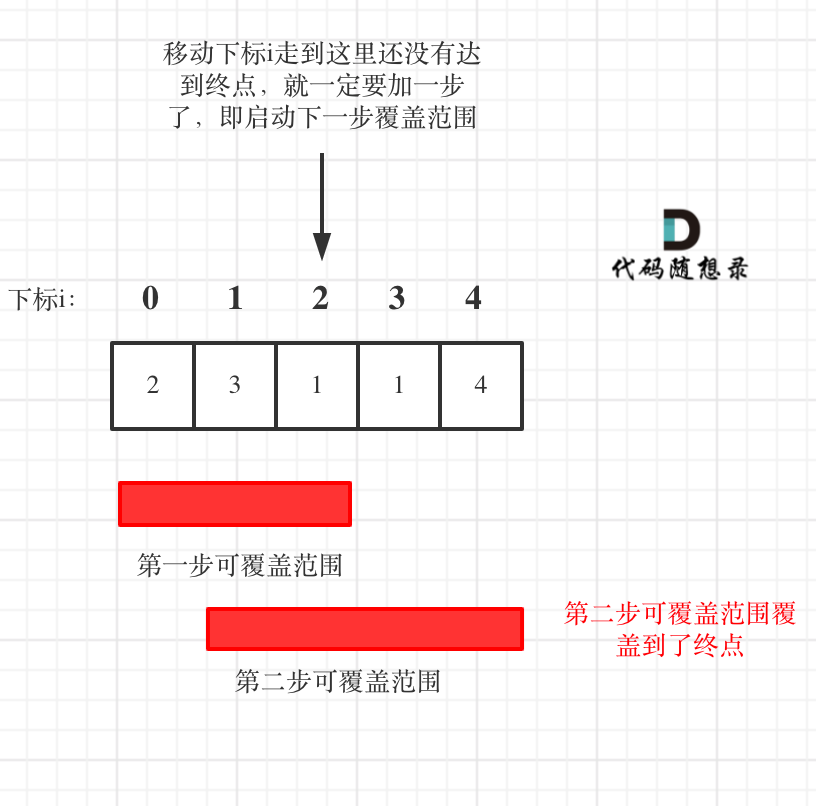
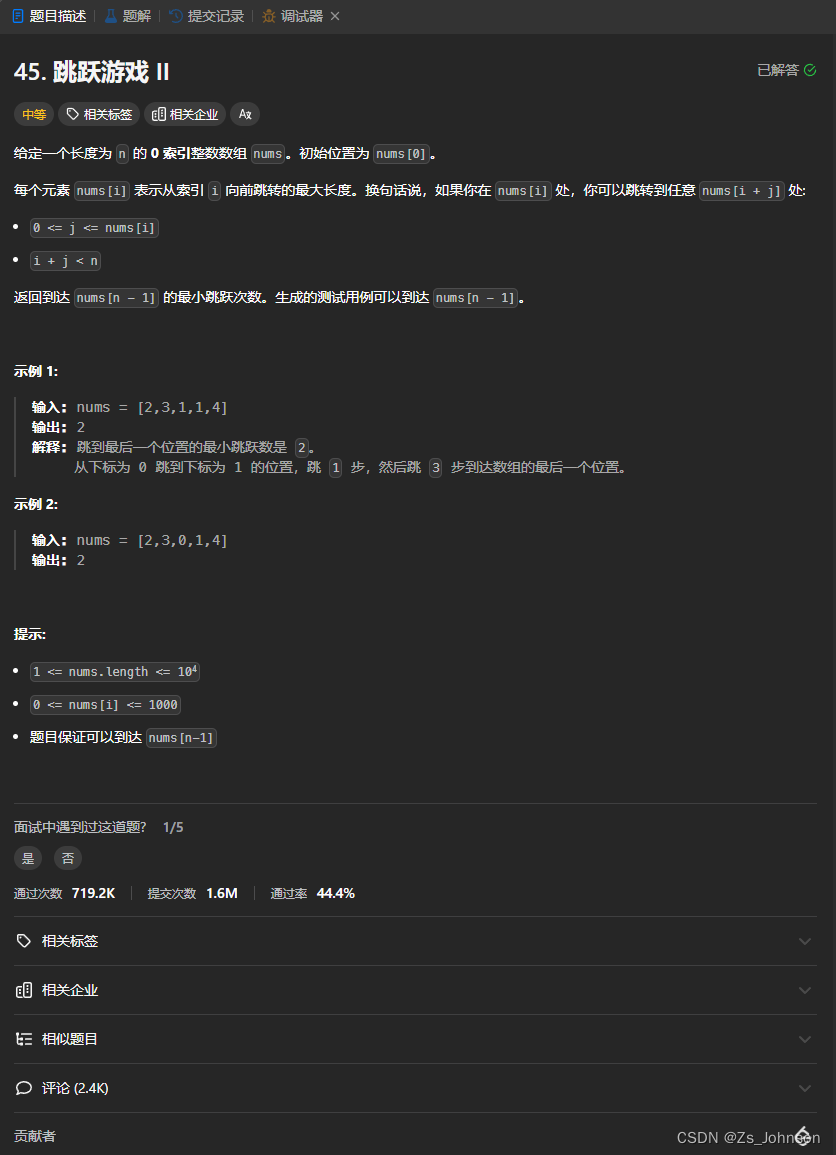
45. 跳跃游戏 II 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处: 0 <= j <= nums[i] i + j < n 返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 n
贪心算法---跳跃游戏(2)
题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处: 0 <= j <= nums[i] i + j < n 返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]
代码随想录算法训练营day28 | 贪心算法 | 122.买卖股票的最佳时机 II、55.跳跃游戏、45.跳跃游戏 II、1005.K次取反后最大化的数组和
文章目录 122.买卖股票的最佳时机 II思路 55.跳跃游戏思路解法1解法2 45.跳跃游戏 II思路 1005.K次取反后最大化的数组和思路 总结 今天是贪心算法专题的第二天,直接上题目 122.买卖股票的最佳时机 II 题目链接:122. 买卖股票的最佳时机 II - 力扣(LeetCode) 思路 思想很简单:把所有的涨幅都赚到,把所有的跌幅都躲过,最后就能获
LeetCode.55.跳跃游戏(贪心算法思路)
题目描述: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 输入输出实例: 思路:要判断最后我们是否能到达最后一个位置,我们可以选择遍历数组,使用贪心的思路,找在每个位置时能到达的最远距离,最开始我们在0,可以达到的最远距离为nums[0
力扣面试经典算法150题:跳跃游戏 II
跳跃游戏 II 今天的题目是力扣面试经典150题中的数组的中等难度题:跳跃游戏II。 题目链接:https://leetcode.cn/problems/jump-game-ii/description/?envType=study-plan-v2&envId=top-interview-150 题目描述 给定一个非负整数数组 nums,你最初位于数组的第一个位置。每个元素代表你在该
力扣面试经典算法150题:跳跃游戏
跳跃游戏 今天的题目是力扣面试经典150题中的数组的中等难度题:跳跃游戏。 题目链接:https://leetcode.cn/problems/jump-game/description/?envType=study-plan-v2&envId=top-interview-150 题目描述 给定一个非负整数数组 nums,你最初位于数组的 第一个下标,即 nums[0] 。数组中的每
力扣爆刷第174天之TOP200五连刷136=140(最小k数、字典序、跳跃游戏)
力扣爆刷第174天之TOP200五连刷136=140(最小k数、字典序、跳跃游戏) 文章目录 力扣爆刷第174天之TOP200五连刷136=140(最小k数、字典序、跳跃游戏)一、LCR 159. 库存管理 III二、450. 删除二叉搜索树中的节点三、440. 字典序的第K小数字四、LCR 127. 跳跃训练五、45. 跳跃游戏 II 一、LCR 159. 库存管理 III
跳跃表-随机化数据结构
Skip list(跳表)是一种可以代替平衡树的数据结构 参考 http://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/Map/skip-list-impl.html http://www.acmerblog.com/skip-list-impl-java-5773.html Skip list的性质 (1) 由很多层结构组成,l
小山菌_代码随想录算法训练营第三十天|122.买卖股票的最佳时机II、55. 跳跃游戏 、45.跳跃游戏II、1005.K次取反后最大化的数组和
122.买卖股票的最佳时机II 文档讲解:代码随想录.买卖股票的最佳时机II 视频讲解:贪心算法也能解决股票问题!LeetCode:122.买卖股票最佳时机II 状态:已完成 代码实现 class Solution {public:int maxProfit(vector<int>& prices) {int result = 0;for (int i = 1; i < prices
TOP150-LC45-跳跃问题II-java版
java解法-贪心 /*跳跃游戏II给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:0 <= j <= nums[i]i + j < n返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nu
用正弦函数实现跳跃弧线
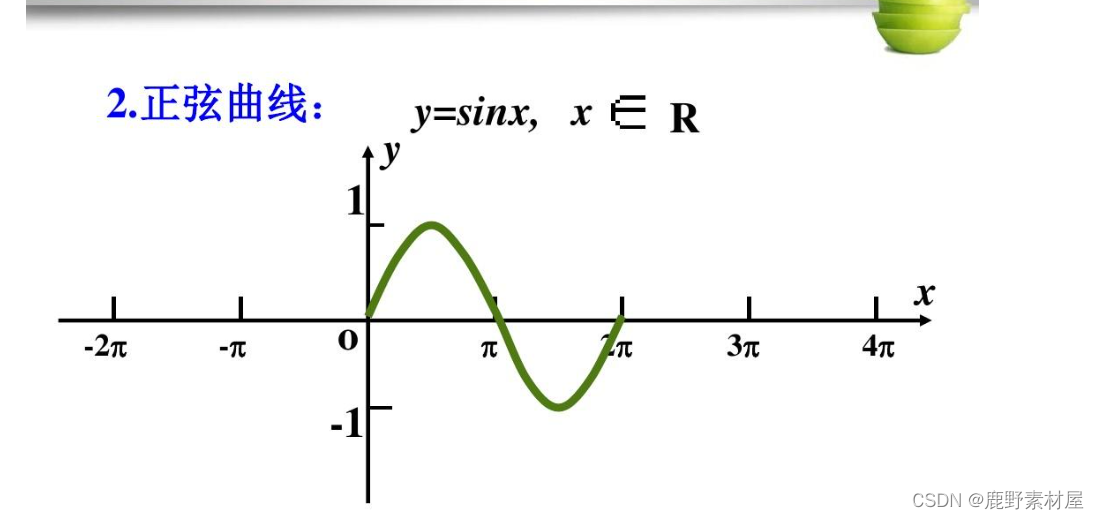
1,想法来源 在游戏中,需要实现一个跳跃的功能,我最开始用的是重力加速度。即水平速度不变,垂直速度加等于重力,但策划觉得不好调。 最后决定使用固定的曲线函数实现,即X轴速度不变,Y轴按照距离最高点的距离求位置。 这样就可以就联想到了正弦函数。 2,正弦函数 标准的正弦函数如下: 代码实现如下: double a = 30; // converting value to radi
癫狂头歌动态规划之跳跃问题Python
第一关跳跃问题 这里我照着图片的代码敲市过不去,真够癫狂的 def CollectValues():n, m = map(int, input().split()) #获得输入信息p = [list(map(int, input().split())) for i in range(n)] #获得输入信息dp = [[-10000] * m for i in range(n)] #初始化
day32贪心算法part02| 122.买卖股票的最佳时机II 55. 跳跃游戏 45.跳跃游戏II
122.买卖股票的最佳时机II 本题解法很巧妙,大家可以看题思考一下,在看题解。 题目讲解 | 题目链接 class Solution {public:int maxProfit(vector<int>& prices) {int result = 0;for (int i = 1; i < prices.size(); i++) {// 直接看两天之间的差值,将所有为正的加和int p
100道面试必会算法-34-跳跃游戏 跳跃游戏
100道面试必会算法-34-跳跃游戏 | && 跳跃游戏|| 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处: 0 <= j <= nums[i]i + j < n 返回到达 nums[n - 1] 的最小跳跃
代码随想录算法训练营第三十二天| 122.买卖股票的最佳时机II,55. 跳跃游戏 ,45.跳跃游戏II
122. 买卖股票的最佳时机 II - 力扣(LeetCode) class Solution {public int maxProfit(int[] prices) {if(prices.length == 0){return 0;}int min = prices[0];int result = 0;for(int i=1;i<prices.length;i++){if(
C++ 贪心算法——跳跃游戏、划分字母区间
一:跳跃游戏 55. 跳跃游戏 题目描述:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输入:nums = [2,3,1,1,4]输出:true解释:可以先跳 1 步,从下标 0 到
【代码随想录算法训练Day32】122.买卖股票的最佳时机 55.跳跃游戏 45.跳跃游戏II
122.买卖股票的最佳时机 II 最开始的思路是为了获得最大利益,低买高卖,在所有的低点都尝试购买,碰到更低的点,就把之前的抛掉,从新购买低点,然后我们要将所有挣钱的时候值都加起来。 将数组的值转成柱状图或则折线图来看,我们想要的就是所有的上升部分的值,所以在遍历时判断当前元素是否比前一个大,大则可以更新在这个点时上升的线段的最大值。在碰到下降的线段,即当前值比上一个值小的时候,说明前面的上升
贪心算法 之 股票 跳跃游戏1and2
第一题: 给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。 返回 你能获得的 最大 利润 。 示例 1: 输入:prices = [7,1,5,3,6,4]输出:7解释:在第 2 天(股票价格 = 1)的时候买入,
贪心算法跳跃游戏1and2
题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输入:nums = [2,3,1,1,4]输出:true解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
【代码随想录算法训练Day32】LeetCode 122 买卖股票的最佳时机 II、LeetCode 55.跳跃游戏、LeetCode 45.跳跃游戏II
Day32 贪心第二天 LeetCode 122 买卖股票的最佳时机 II 思路真是无比巧妙,把区间利润拆成每天的利润,其实就是算出每天的利润,然后只取其中的正值即可。 在代码中计算是否计算加时还与0取最大值,相当于大于0才加入。 class Solution {public:int maxProfit(vector<int>& prices) {int res=0;for(int i=1

![2024.9.1 Python,跳跃游戏,贪心算法,回溯算法复原 IP 地址,关于回溯过程中列表的[:]以及copy问题再讨论](/front/images/it_default2.jpg)