跳跃表-随机化数据结构

2024-06-22 20:58
文章标签 随机化 数据结构 跳跃

本文主要是介绍跳跃表-随机化数据结构，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Skip list(跳表）是一种可以代替平衡树的数据结构

参考
http://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/Map/skip-list-impl.html

http://www.acmerblog.com/skip-list-impl-java-5773.html

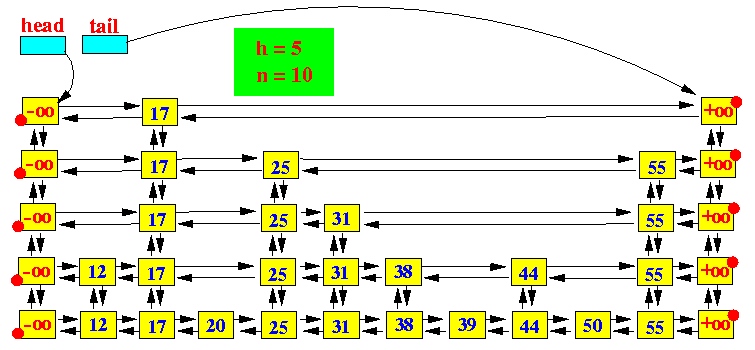
Skip list的性质

(1) 由很多层结构组成，level是通过一定的概率随机产生的。
(2) 每一层都是一个有序的链表，默认是升序
(3) 最底层(Level 1)的链表包含所有元素。
(4) 如果一个元素出现在Level i 的链表中，则它在Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

这里写图片描述

Java代码实现：

  1. SkipListEntry.java ， 这是跳跃表中存储的每个元素实体类，包含 上下左右 四个指针。
package skiplist;public class SkipListEntry {public String key;public Integer value;public int pos;public SkipListEntry up, down, left, right;public static String negInf = new String("-oo");public static String posInf = new String("+oo");public SkipListEntry(String k, Integer v){key = k;value = v;up = down = left = right = null;}public String getKey() {return key;}public void setKey(String key) {this.key = key;}public Integer getValue() {return value;}public Integer setValue(Integer value) {Integer OldValue = value;this.value = value;return OldValue;}@Overridepublic boolean equals(Object obj) {SkipListEntry ent;try{ent = (SkipListEntry) obj;} catch (ClassCastException ex){return false;}return (ent.getKey() == key) && (ent.getValue() == value);}@Overridepublic String toString() {return "SkipListEntry [key=" + key + ", value=" + value + "]";}}

2 SkipList.java, 跳跃表类，包含算法的实现。 head 和 tail 分别是 顶层的头和尾。

package skiplist;import java.util.Random;public class SkipList {public SkipListEntry head;public SkipListEntry tail;public int n; // 跳跃表中元素的个数public int h; // 跳跃表的高度public Random r;public SkipList(){SkipListEntry p1,p2;p1 = new SkipListEntry(SkipListEntry.negInf, null);p2 = new SkipListEntry(SkipListEntry.posInf, null);head = p1;tail = p2;p1.right = p2;p2.left = p1;n = 0;h = 0;r = new Random();}/** 返回包含元素的个数  */public int size(){return n;}/** 跳跃表是否为空 */public  boolean isEmpty(){return (n == 0);}/** 在最下面一层， 找到要插入的位置前面的哪个key*/public SkipListEntry findEntry(String k){SkipListEntry p;p = head;while(true){while( p.right.key != SkipListEntry.posInf && p.right.key.compareTo(k) <= 0){p = p.right;}if(p.down != null){p = p.down;}else{break;}}return p;}/** 返回和key绑定的值 */public Integer get(String k){SkipListEntry p;p = findEntry(k);if (k.equals(p.getKey())){return p.value;}else{return null;}}/** 放一个key-value到跳跃表中 ，替换原有的并返回*/public Integer put(String k , Integer v){SkipListEntry p, q;int i;/** 找到key 就返回原值， 将新值替换进链表 */p = findEntry(k);if(k.equals(p.getKey())){Integer old = p.value;p.value = v;return old;}/** 如果没有找到新值，就新建一个 */q = new SkipListEntry(k, v);q.left = p;q.right = p.right;p.right.left = q;p.right = q;i = 0;while(r.nextDouble() < 0.5){//如果超出了高度，需要重新建一个顶层if (i >= h) {SkipListEntry p1, p2;h = h + 1;p1 = new SkipListEntry(SkipListEntry.negInf, null);p2 = new SkipListEntry(SkipListEntry.posInf, null);p1.right = p2;p1.down = head;p2.left = p1;p2.down = tail;head.up = p1;tail.up = p2;head = p1;tail = p2;}// 将p移动到 最左边while(p.up == null){p = p.left;}p = p.up;SkipListEntry e;e = new SkipListEntry(k, null); e.left = p;e.right = p.right;e.down = q;p.right.left = e;p.right = e;q.up = e;q = e; // q 进行下一层迭代i = i + 1; // 当前层 +1}n = n + 1;return (null);}public Integer remove(String key) {return (null);}public void printHorizontal() {String s = "";int i;SkipListEntry p;p = head;while (p.down != null) {p = p.down;}i = 0;while (p != null) {p.pos = i++;p = p.right;}p = head;while (p != null) {s = getOneRow(p);System.out.println(s);p = p.down;}}//用了打印测试public String getOneRow(SkipListEntry p) {String s;int a, b, i;a = 0;s = "" + p.key;p = p.right;while (p != null) {SkipListEntry q;q = p;while (q.down != null)q = q.down;b = q.pos;s = s + " <-";for (i = a + 1; i < b; i++)s = s + "--------";s = s + "> " + p.key;a = b;p = p.right;}return (s);}//用了打印测试public void printVertical() {String s = "";SkipListEntry p;p = head;while (p.down != null)p = p.down;while (p != null) {s = getOneColumn(p);System.out.println(s);p = p.right;}}//用了打印测试public String getOneColumn(SkipListEntry p) {String s = "";while (p != null) {s = s + " " + p.key;p = p.up;}return (s);}
}

3 测试类，Test.java

package skiplist;public class Test {public static void main(String[] args) {SkipList S = new SkipList();S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");S.put("ABC", 123);S.printHorizontal();System.out.println("------");// S.printVertical();//System.out.println("======");S.put("DEF", 123);S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");S.put("KLM", 123);S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");S.put("HIJ", 123);S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");S.put("GHJ", 123);S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");S.put("AAA", 123);S.printHorizontal();System.out.println("------");// S.printVertical();// System.out.println("======");}
}

输出结果

-oo <-> +oo
------
-oo <-> ABC <-> +oo
------
-oo <-> ABC <-> DEF <-> +oo
------
-oo <-----------------> KLM <-> +oo
-oo <-> ABC <-> DEF <-> KLM <-> +oo
------
-oo <-----------------> HIJ <---------> +oo
-oo <-----------------> HIJ <---------> +oo
-oo <-----------------> HIJ <---------> +oo
-oo <-----------------> HIJ <-> KLM <-> +oo
-oo <-> ABC <-> DEF <-> HIJ <-> KLM <-> +oo
------
-oo <-------------------------> HIJ <---------> +oo
-oo <-------------------------> HIJ <---------> +oo
-oo <-----------------> GHJ <-> HIJ <---------> +oo
-oo <-----------------> GHJ <-> HIJ <-> KLM <-> +oo
-oo <-> ABC <-> DEF <-> GHJ <-> HIJ <-> KLM <-> +oo
------
-oo <---------------------------------> HIJ <---------> +oo
-oo <---------------------------------> HIJ <---------> +oo
-oo <-------------------------> GHJ <-> HIJ <---------> +oo
-oo <-------------------------> GHJ <-> HIJ <-> KLM <-> +oo
-oo <-> AAA <-> ABC <-> DEF <-> GHJ <-> HIJ <-> KLM <-> +oo
------

这篇关于跳跃表-随机化数据结构的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1085392。

相关文章

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

8.3 交换排序 8.3.1 冒泡排序 【算法特点】 (1) 稳定排序。 (2) 可用于链式存储结构。 (3) 移动记录次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时， 此算法不宜采用。 #include <stdio.h>#include <stdlib.h>#define MAXSIZE 26typedef int KeyType;typedef char In
阅读更多...
【408数据结构】散列 （哈希）知识点集合复习考点题目

【408数据结构】散列 （哈希）知识点集合复习考点题目

苏泽  “弃工从研”的路上很孤独，于是我记下了些许笔记相伴，希望能够帮助到大家    知识点 1. 散列查找 散列查找是一种高效的查找方法，它通过散列函数将关键字映射到数组的一个位置，从而实现快速查找。这种方法的时间复杂度平均为(
阅读更多...
浙大数据结构：树的定义与操作

浙大数据结构：树的定义与操作

四种遍历 #include<iostream>#include<queue>using namespace std;typedef struct treenode *BinTree;typedef BinTree position;typedef int ElementType;struct treenode{ElementType data;BinTree left;BinTre
阅读更多...
Python 内置的一些数据结构

Python 内置的一些数据结构

文章目录 1. 列表 (List)2. 元组 (Tuple)3. 字典 (Dictionary)4. 集合 (Set)5. 字符串 (String) Python 提供了几种内置的数据结构来存储和操作数据，每种都有其独特的特点和用途。下面是一些常用的数据结构及其简要说明： 1. 列表 (List) 列表是一种可变的有序集合，可以存放任意类型的数据。列表中的元素可以通过索
阅读更多...
浙大数据结构：04-树7 二叉搜索树的操作集

浙大数据结构：04-树7 二叉搜索树的操作集

这道题答案都在PPT上，所以先学会再写的话并不难。 1、BinTree Insert( BinTree BST, ElementType X ) 递归实现，小就进左子树，大就进右子树。 为空就新建结点插入。 BinTree Insert( BinTree BST, ElementType X ){if(!BST){BST=(BinTree)malloc(sizeof(struct TNo
阅读更多...
【数据结构入门】排序算法之交换排序与归并排序

【数据结构入门】排序算法之交换排序与归并排序

前言         在前一篇博客，我们学习了排序算法中的插入排序和选择排序，接下来我们将继续探索交换排序与归并排序，这两个排序都是重头戏，让我们接着往下看。  一、交换排序 1.1 冒泡排序 冒泡排序是一种简单的排序算法。 1.1.1 基本思想 它的基本思想是通过相邻元素的比较和交换，让较大的元素逐渐向右移动，从而将最大的元素移动到最右边。 动画演示： 1.1.2 具体步
阅读更多...
数据结构：线性表的顺序存储

数据结构：线性表的顺序存储

文章目录 🍊自我介绍🍊线性表的顺序存储介绍概述例子 🍊顺序表的存储类型设计设计思路类型设计 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以：点赞+关注+评论+收藏（一键四连）哦~ 🍊自我介绍   Hello,大家好，我是小珑也要变强（也是小珑），我是易编程·终身成长社群的一名“创始团队·嘉宾” 和“内容共创官” ,现在我来为大家介绍一下有关物联网-嵌入
阅读更多...
[数据结构]队列之顺序队列的类模板实现

[数据结构]队列之顺序队列的类模板实现

队列是一种限定存取位置的线性表，允许插入的一端叫做队尾（rear），允许删除的一端叫做队首（front）。 队列具有FIFO的性质 队列的存储表示也有两种方式：基于数组的，基于列表的。基于数组的叫做顺序队列，基于列表的叫做链式队列。 一下是基于动态数组的顺序队列的模板类的实现。 顺序队列的抽象基类如下所示：只提供了接口和显式的默认构造函数和析构函数，在派生类中调用。 #i
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2