代码随想录算法训练营day28 | 贪心算法 | 122.买卖股票的最佳时机 II、55.跳跃游戏、45.跳跃游戏 II、1005.K次取反后最大化的数组和

本文主要是介绍代码随想录算法训练营day28 | 贪心算法 | 122.买卖股票的最佳时机 II、55.跳跃游戏、45.跳跃游戏 II、1005.K次取反后最大化的数组和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

今天是贪心算法专题的第二天，直接上题目

122.买卖股票的最佳时机 II

题目链接：122. 买卖股票的最佳时机 II - 力扣（LeetCode）

思路

思想很简单：把所有的涨幅都赚到，把所有的跌幅都躲过，最后就能获得最大利润，这里就有贪心的思想

局部最优：收集每天的正利润，全局最优：求得最大利润

最终的利润是可以分解的，我们把最终利润分解为多个相邻两天的利润之和，比如从第0天买入，第3天卖出，那么利润就是：prices[3] - prices[0]，而不是从第0天到第3天整体去考虑

那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1])…(prices[1] - prices[0])，如图所示：

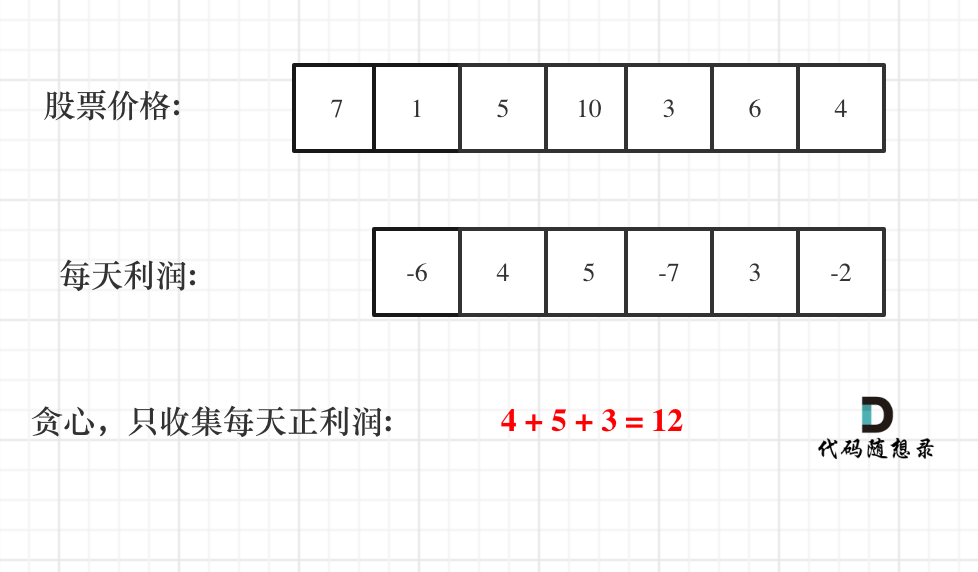
我们只需要收集每天的正利润，正利润的区间就是股票买卖的区间，最终的最大利益就是这些正利润之和

代码实现：

class Solution {
public:int maxProfit(vector<int>& prices) {int result = 0;for(int i=0; i<prices.size()-1; ++i){if(prices[i+1] - prices[i] > 0){result += prices[i+1] - prices[i];}}return result;}
};

55.跳跃游戏

建议：本题如果没接触过，很难想到，所以不要自己憋时间太久，读题思考一会，没思路立刻看题解

题目链接：55. 跳跃游戏 - 力扣（LeetCode）

思路

解法1

从倒数第二个元素开始，向前遍历。如果倒数第二个元素无法到达最后一个元素，那么step++，然后看倒数第三个元素是否能到达最后一个元素（它相比于倒数第二个元素，需要多跳一格，因此step++），若不能，则step++，看倒数第四个元素是否能到达最后一个元素······，如果某个元素k能够完成任务，那么这个元素前面的元素k-1的任务就是跳到元素k，元素k相当于一个中转站，step=1。最后，如果step == 1，那么说明了第一个元素能够跳跃到某个元素i，而元素i又能跳跃到元素j······，最终能跳跃到最后一个元素

class Solution {
public:bool canJump(vector<int>& nums) {int step = 1;for(int i=nums.size()-2; i>=0; --i){if(nums[i] >= step){step = 1;}else{step++;}}return step == 1;}
};

解法2

• 问题分析：不需要明确一次究竟跳几步，每次取最大的跳跃步数nums[i]，研究每次跳跃能覆盖到的范围（i~i+nums[i]），这个范围内的所有位置都是可达的。我们把问题转换为——跳跃覆盖范围是否可以覆盖到终点，即最后一个元素的位置

  • 局部最优：每次移动取最大的跳跃步数（得到最大的覆盖范围）

  • 整体最优：最后得到整体的最大覆盖范围，看是否能到达终点

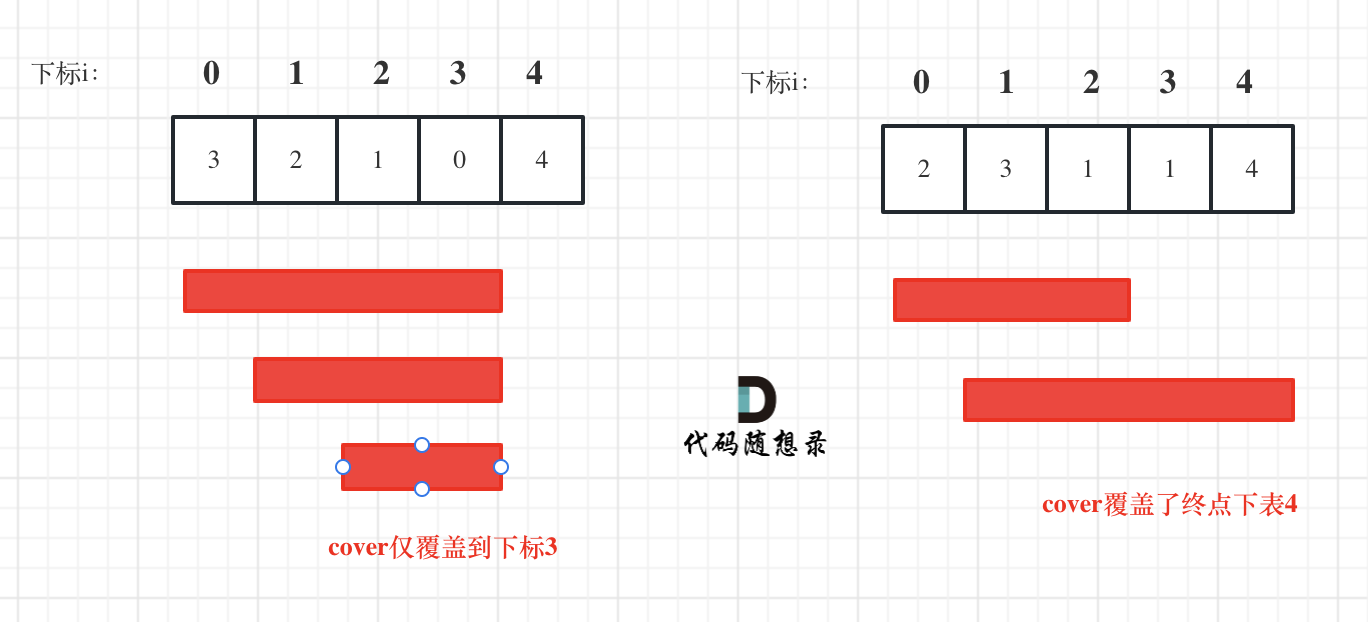
• 整体思路：设当前 能跳跃到的最大下标为cover，下标i只能在cover内移动。每次移动一个单位，然后更新cover，比较当前的cover 和 i+nums[i]的大小，取较大的为新的cover。每次更新cover后，判断 是否到达了最后一个元素的位置，如果cover大于等于终点下标，则return true

  如图：

  

代码实现

class Solution{public:bool canJump(vector<int>& nums){int cover = 0;for(int i=0; i<=cover; ++i)	// 注意这里是小于等于cover，在cover范围内的（包括cover）都是可达的{cover = max(i + nums[i], cover);if(cover >= nums.size() - 1){return true;}}return false;}
};

45.跳跃游戏 II

建议：本题同样不容易想出来。贪心就是这样，有的时候 会感觉简单到离谱，有时候，难的不行，主要是不容易想到

题目链接：45. 跳跃游戏 II - 力扣（LeetCode）

思路

题目要计算所需的最少步数，所以本题的关键是：考虑什么时候步数加一。与上一道题目类似，我们用最大覆盖范围解决这道题目

在上一道题目中，每次下标移动一个单位后就更新cover，计算当前的最大覆盖范围，并判断cover是否覆盖到了最后一个元素的位置。对于本题，我们需要考虑两个覆盖范围：设当前这一步能够跳跃到的最大下标为curDistance，下一步能够跳跃到的最大下标为nextDistance，就像火箭逐级递推一样，我们希望每一步的跳跃范围都尽可能大，从而离终点尽可能近，这就用到了贪心思想。nextDistance 是 当前这一步的最大跳跃范围中，i+nums[i]的最大值，这样，下一步的跳跃范围也尽可能大了

整个过程是这样的：如果当前这一步的最大跳跃范围不能包括终点，则至少要再跳跃一步，在遍历当前的最大跳跃范围的过程中，我们要获得i+nums[i]的最大值，它是下一步能跳跃到的最大下标值nextDistance，也就是下一步的最大跳跃范围。每一步的最大跳跃范围都尽可能大，那么用几段最大跳跃范围就能覆盖整个数组，每一段都对应着一次跳跃。如图：

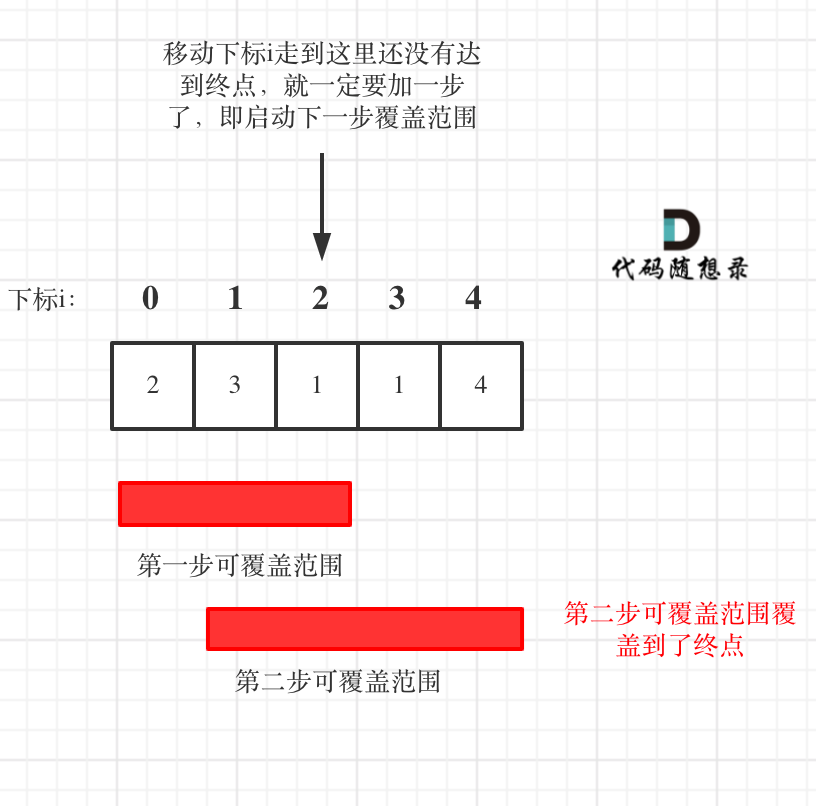
第一步我们最远能跳跃到下标2。当前这一步的最大跳跃范围为0~2，不包括终点4，因此要至少再跳跃一步，需要计算下一步的最大跳跃范围。在第一步的最大跳跃范围中，当i=1时，i+nums[i]取到最大值为4，第二步的最大跳跃范围包括了终点4，因此最少的跳跃步数为2

代码实现

class Solution {
public:int jump(vector<int>& nums) {if (nums.size() == 1) return 0;int curDistance = 0;    // 当前覆盖最远距离下标int ans = 0;            // 记录走的最大步数int nextDistance = 0;   // 下一步覆盖最远距离下标for (int i = 0; i < nums.size(); i++) {nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标if (i == curDistance) {                         // 遇到当前覆盖最远距离下标ans++;                                  // 需要走下一步curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）if (nextDistance >= nums.size() - 1) break;  // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束}}return ans;}
};

1005.K次取反后最大化的数组和

题目链接：1005. K 次取反后最大化的数组和 - 力扣（LeetCode）

思路

思想很简单，但是用了两次贪心

第一次贪心：当前数组有正有负，如何让数组和最大？局部最优：我们让绝对值大的负数变为正数，让当前的数值达到最大；全局最优：整个数组和达到最大

第二次贪心：如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大？这又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大

代码实现

1. 按照绝对值大小，降序排列A
2. 从前到后遍历A，将数组中的负数变为正数，同时K–
3. 如果K还大于0，那么反复转变绝对值最小的元素A[A.size()-1]
4. 求和

class Solution
{static bool cmp(int a, int b){return abs(a) > abs(b);     // 如果a的绝对值大于b的绝对值，则a排序在前}public:int largestSumAfterKNegations(vector<int>&A, int K){sort(A.begin(), A.end(), cmp);	// 首先按照绝对值大小降序排序Afor(int i=0; i<A.size(); ++i){if(A[i] < 0 && K > 0)	// 首先对A中的负数变号{A[i] *= -1;K--;}}if(K % 2 == 1){A[A.size()-1] *= -1;	// 如果K仍大于0，则将绝对值最小的元素反复变号}int result = 0;for(int a : A){result += a;}return result;}
};

总结

一定要有贪心的思考方式：考虑局部最优，全局最优。使用贪心解决一个问题，在解决过程中，整个问题被分成两个部分：一部分已经用贪心求得最优解，这是贪心选择性所保证的；另一部分是还没有解决的子问题，根据最优子结构，我们也可以用一样的贪心方法 获得它的最优解。贪心的过程是只考虑当前的最优情况，然后遗留下一个规模变小了，但性质相同的子问题，如果贪心选出的是最优解，则本次贪心选出来的解一定是最终的最优解的一部分；剩下的子问题中的最优解与刚贪心选出来的解可以凑成原问题的最优解

如果没有贪心的思考方式（局部最优，全局最优），很容易陷入贪心简单题凭感觉做，贪心难题直接不会做，其实这样就锻炼不了贪心的思考方式了。

回顾一下这四道题：

• 122.买卖股票的最佳时机 II

  • 局部最优：收集每天的正利润，获得前i天的最大利润
  • 整体最优：获得这n天的最大利润

• 55.跳跃游戏

  • 局部最优：每次移动取最大的跳跃步数（得到最大的覆盖范围），即保证获得每次的最大跳跃覆盖范围

  • 整体最优：最后得到整体的最大覆盖范围，看是否能到达终点

  难点是想到利用最大跳跃覆盖范围实现贪心

• 45.跳跃游戏 II

  • 局部最优：每一步的跳跃覆盖范围都尽可能大，从而离终点尽可能近
  • 整体最优：用最少段跳跃范围覆盖整个数组，从而使跳跃步数最少

• 1005.K次取反后最大化的数组和

  数组有正有负

  • 局部最优：让绝对值大的负数变为正数，让当前的数值达到最大
  • 整体最优：整个数组和达到最大

  数组是非负序列

  • 局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了）
  • 整体最优：整个数组和达到最大

即使是贪心简单题，也要靠贪心的思考方式来解题，这样对培养解题感觉很有帮助

这篇关于代码随想录算法训练营day28 | 贪心算法 | 122.买卖股票的最佳时机 II、55.跳跃游戏、45.跳跃游戏 II、1005.K次取反后最大化的数组和的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---