蒙特卡罗专题
蒙特卡罗模拟之排队上厕所问题
蒙特卡罗模拟之排队上厕所问题 '''电影结束后会有20人上厕所20个人会在0-10分钟内全部到达厕所每个人上厕所时间在1-3分钟模拟只有一个厕所到达时间，等待时间，开始上厕所时间，结束时间'''import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib.patches
![【Hadoop】-拓展：蒙特卡罗算法求PI的基础原理[10]](https://img-blog.csdnimg.cn/direct/dc2b4349c1fb45c9a5db65130bebefba.png)
【Hadoop】-拓展：蒙特卡罗算法求PI的基础原理[10]
Monte Carlo蒙特卡罗算法（统计模拟法） Monte Carlo算法的基本思想是：以模拟的“实验”形式、以大量随机样本的统计形式，来得到问题的求解。比如，求圆周率，以数学的方式是非常复杂的，但是我们可以以简单的形式去求解： 如图，我们在正方形内，随机落点，统计落在1/4圆内的点和总店数量的比例即可得到1/4的PI，最终乘以4即可得到PI。比如，红色点的数量比全部点的数量，结果是
![[定位算法]amcl（自适应蒙特卡罗定位）](https://img-blog.csdnimg.cn/20181227143603580)
[定位算法]amcl（自适应蒙特卡罗定位）
AMCL amcl采用的是结合自适应（增强蒙特卡洛Augmented_MCL）和库尔贝克-莱不勒散度采样KLD_Sampling_MCL（蒙特卡洛定位的一个变种）。 1.KLD_Sampling_MCL随时间改变粒子数，改良了度过初期后的蒙特卡洛大样本集合的资源浪费。两个kld_配置参数就是KLD的参数。对于每次粒子滤波迭代，KLD采样以概率1-δ确定样本数（1-δ就是kld_z配置参数），使得
数学建模--蒙特卡罗法MATLAB代码保姆式解析
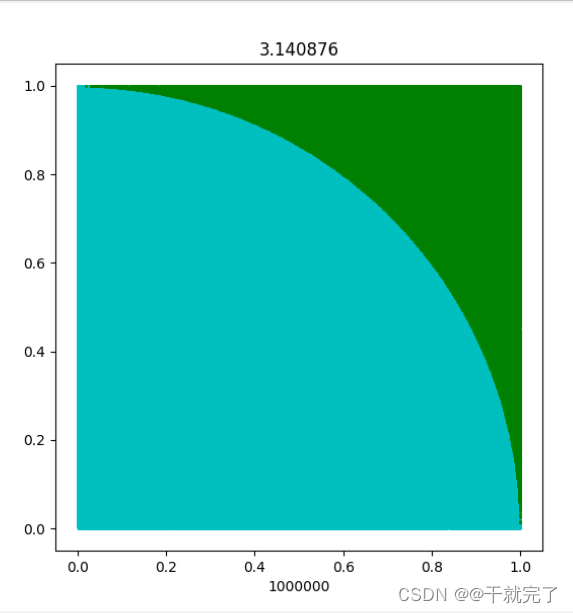
1.简单介绍 2.思想的实际运用 我们利用蒙特卡罗法的思想求解圆周率π的值，这里求得的肯定是近似值，我们是通过大量的模拟实验，利用概率求解的，但是这个值和我们的精确值之间还是有一定的误差的； 我们的思想就是在半径为1的圆的外面做一个外切正方形，这个外切正方形的边长就是2，那么我们想要求的圆的面积π乘上半径的平方实际上就是乘以1的平方，也就是说圆的面积就是π，我们在
【通信仿真】基于matlab蒙特卡罗算法2FSK系统抗噪声性能仿真【含Matlab源码 1632期】
⛄一、获取代码方式 获取代码方式1： 完整代码已上传我的资源：【通信仿真】基于matlab蒙特卡罗算法2FSK系统抗噪声性能仿真【含Matlab源码 1632期】 点击上面蓝色字体，直接付费下载，即可。 获取代码方式2： 付费专栏Matlab信号处理（初级版） 备注： 点击上面蓝色字体付费专栏Matlab信号处理（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab信
统计学_蒙特卡罗方法
1、蒙特卡罗方法的基本思想 蒙特卡罗方法(Monte Carlo method)是由冯诺依曼和乌拉姆等人发明的，“蒙特卡罗”这个名字是出自摩纳哥的蒙特卡罗赌场，这个方法是一类基于概率的方法的统称，不是特指一种方法。 蒙特卡罗方法也成统计模拟方法，是指使用随机数（或者更常见的伪随机数）来解决很多计算问题的方法。他的工作原理就是两件事：不断抽样、逐渐逼近。下面用两个例子[1]来理解一下这个方法的思
【机器学习】蒙特卡罗算法 整理
蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）
MATLAB练习题：利用蒙特卡罗模拟来计算圆周率π
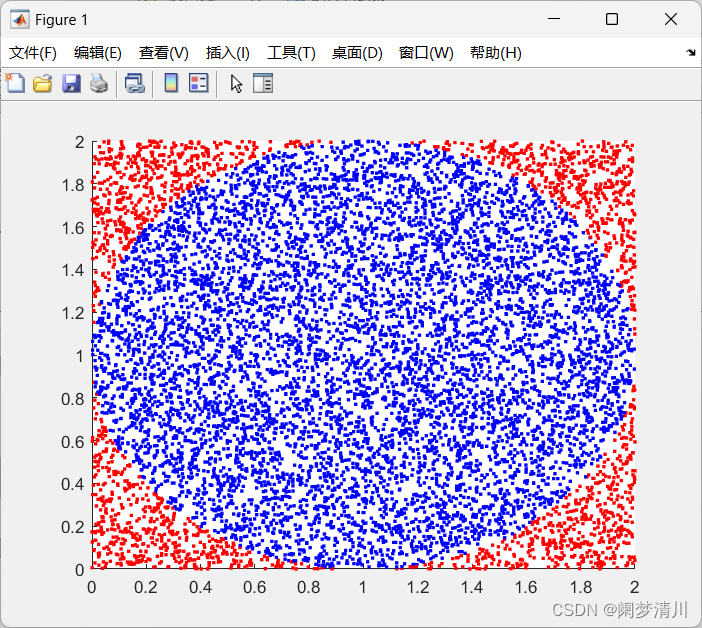
讲解视频：可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇（数学建模清风主讲，适合零基础同学观看）_哔哩哔哩_bilibili 蒙特卡罗模拟是一种以概率和统计理论为基础的计算方法，它能通过随机数来解决很多计算问题。蒙特卡罗模拟将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解。本题将利用蒙特卡
蒙特卡罗算法计算圆周率PI（C++）
蒙特卡罗（Monte Carlo）算法计算圆周率的主要思想：给定边长为R的正方形，画其内切圆，然后在正方形内随机打点，设点落在圆内的概为P，则根据概率学原理： P = 圆面积 / 正方形面积 ＝ PI * R * R / 2R * 2R = PI / 4。 即 PI=4P。这样，当随机打点足够多时，统计出来的概率就非常接近于PI的四分之一了。 #include <iostream>#inclu
再学概率论-蒙特卡罗和拉斯维加斯
对于喜欢看片的人来说，拉斯维加斯是再熟悉不过了，这座以赌城闻名的城市几乎出现在很多的赌类电影中，而蒙特卡罗也是一个赌城。这里之所以和算法相关联，主要在于概率论最早的使用领地就是赌场之中，而蒙特卡罗算法和拉斯维加斯算法就是其中两种算法的核心原理。 蒙特卡罗 为了更加形象的说明两个算法的原理，我们先举一个例子，以防迷失在过多的公式之中。 蒙特卡罗：假如你是一个赌徒，你经常去玩转轮盘游戏，轮盘
为什么时序差分是动态规划和蒙特卡罗的结合
动态规划的优势：在已知状态转换概率和回报函数的情况下，不需要与环境的交互，直接通过策略迭代或值迭代方法得到最优策略。 动态规划的劣势：但实际情况下，环境的状态转换概率通常是未知的，因此该方法并不实际可行。 动态规划分析：虽然动态规划并不实际可行，但重要的是它的思想：用空间换时间，存储每个状态的值函数（也就是Q表），并利用后继状态的值函数估计当前值函数，这样就实现了单步更新，提升了更新的效率，也
利用蒙特卡罗法算PI，并绘制曲线图和散点图
原理 落在圆内的概率=圆与正方形面积之比=0.25Π 先上图 绘制折线图 import randomimport matplotlib.pyplot as plt#原理 落在圆内的概率=圆与正方形面积之比=0.25Π# total指代在圆里面晒的豆子数def pi(total):count = 0for i in range(total):x = random.random()
【GPU】Nvidia CUDA 编程高级教程——利用蒙特卡罗法求解 的近似值
博主未授权任何人或组织机构转载博主任何原创文章，感谢各位对原创的支持！ 博主链接 本人就职于国际知名终端厂商，负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作，目前牵头6G算力网络技术标准研究。 博客内容主要围绕： 5G/6G协议讲解 算力网络讲解（云计算，边缘计算，端计算） 高级C语言讲解 Rust语言讲解
期权专题9：雪球期权（一）（BSM+蒙特卡罗定价）
目录 1. 前期介绍 1.1 定价思路 1.2 雪球要素 1.3 标的定价 2. 代码复现 2.1 价格路径 2.1.1 单次路径 2.1.2 多次路径 2.2 雪球定价 2.2.1 加入要素 2.2.2 估值定价 3. 完整代码 雪球期权是近两年来备受青睐的衍生品投资标的之一，几个月前就想写一篇关于它的文章。但是因为其定价模型确实比较复杂，无论在思
学习深度强化学习---第3部分----RL蒙特卡罗相关算法
文章目录 3.1节 蒙特卡罗法简介3.2节 蒙特卡罗策略评估3.3节 蒙特卡罗强化学习3.4节 异策略蒙特卡罗法 本部分视频所在地址：深度强化学习的理论与实践 3.1节 蒙特卡罗法简介 在其他学科中的蒙特卡罗法是一种抽样的方法。 如果状态转移概率是已知的，则是基于模型的方法。如果状态转移概率是未知的，则是免模型的方法。动态规划方法无法求解倒立摆问题，即无法处理没有状态转移概率
学习深度强化学习---第3部分----RL蒙特卡罗相关算法
文章目录 3.1节 蒙特卡罗法简介3.2节 蒙特卡罗策略评估3.3节 蒙特卡罗强化学习3.4节 异策略蒙特卡罗法 本部分视频所在地址：深度强化学习的理论与实践 3.1节 蒙特卡罗法简介 在其他学科中的蒙特卡罗法是一种抽样的方法。 如果状态转移概率是已知的，则是基于模型的方法。如果状态转移概率是未知的，则是免模型的方法。动态规划方法无法求解倒立摆问题，即无法处理没有状态转移概率
MATLAB运动学之蒙特卡罗法求积分与机器人工作域分析
蒙特卡罗法又叫做统计模拟法、随机抽样技术，是一种随机模拟方法以概率和统计理论方法为基础的一种计算方法，通俗来说是可以使用随机数来解决很多计算问题的一种方法，很直观简单，尤其对于一些求解积分无解的情况，非常好使且简单粗暴。 蒙特卡罗法求面积（定积分） 以 y = x² 为例，我们需要求出 x 在[0,10]相对应的 y 在[0,100] 所围成的曲线面积，在我们有了微积分的知识之后，我们可以通过
LLM之Prompt（三）| XoT：使用强化学习和蒙特卡罗树搜索将外部知识注入Prompt中，性能超过CoT，ToT和GoT
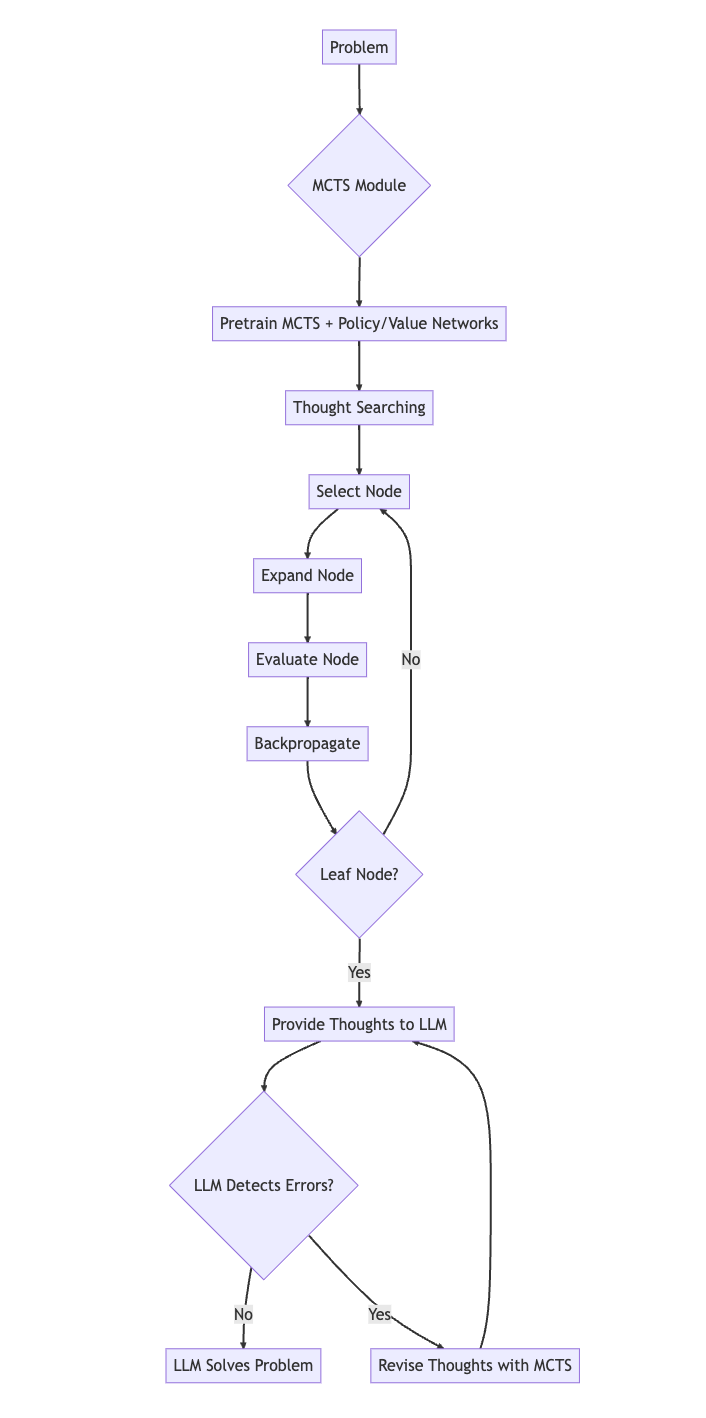
论文地址：https://arxiv.org/pdf/2311.04254.pdf 一、当前Prompt技术的局限性 LLM使用自然语言Prompt可以将复杂的问题分解为更易于管理的“thought”可以回复用户的问题。然而，大多数现有的Prompt技术都有局限性： 输入输出（IO）Prompt：仅适用于具有单步解决方案的简单问题，它缺乏灵活性；思维链（CoT）：能够
浮点计算数值误差及PI的蒙特卡罗近似计算
看JAVA语言程序设计基础，因为以前学习的都是C++, 总体基本上相似。不过这本书里有几个比较有意思的小地方，比如书中写的最小化数值误差(4.7)，书中说在大数之前先增加小数是减少误差的方法。如： //第一种方法求0.01到1之间递增的数列之和for(float i = 0.01f; i<= 1.0f; i = i + 0.01f){sum +=i;}//第二种for(double
R语言 几何概型计算积分 蒙特卡罗方法
设计几何概型实验，估算积分的值 代码 详细解释在代码注释中 # 定义一个函数，该函数为所求的积分函数# 因此在计算上述定积分和计算sqrt(2)同理# 在此用例为sqrt(2)f = function(x)sqrt(2)# 生成xx = seq(1.5, 3.5, length=100)y = rep(0, length(x))j = 1# 计算每个x对应的y值for
由掺杂剂波动引起的阈值变化的蒙特卡罗建模
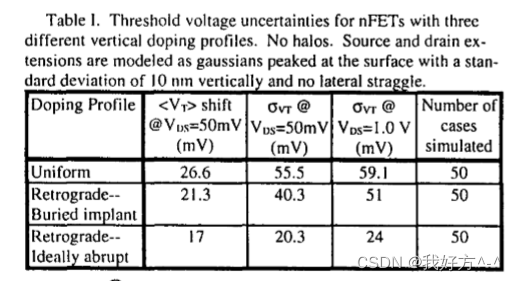
摘要 本文介绍了一种新的 3-D 蒙特卡罗方法，用于模拟 MOSFET 中的随机掺杂剂波动效应。 该方法考虑了器件中的每个硅原子，并且通常适用于任意不均匀的掺杂分布。 除体掺杂波动外，首次研究了源漏掺杂波动对短沟道阈值电压的影响。 结果清楚地表明了逆行体掺杂和浅/突变源漏结的好处。 它还量化了优化设计的 25 nm MOSFET 中由于离散掺杂剂波动引起的阈值电压变化幅度。 介绍 MOSFE
java蒙特卡罗求主元素_0049算法笔记——【随机化算法】蒙特卡罗算法,主元素问题,素数测试问题...
1、蒙特卡罗算法 基本概述 蒙特卡罗(Monte Carlo)方法，又称随机抽样或统计试验方法。传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。 在实际应用中常会遇到一些问题，不论采用确定性算法或随机化算法都无法保证每次都能得到正确的解答。蒙特卡罗算法则在一般情况下可以保证对问题的所有实例
粒子滤波器/卡尔曼滤波局限/状态空间模型/蒙特卡罗方法/重要性采样/重要密度函数/重采样/粒子退化 的核心思想+ Matlab代码
--》是递归贝叶斯滤波的一种实现 --》以高计算量为代价换取能表示任何一种分布形式 --》用随机样本表示，用一组加权样本表示后验 --》在局部化的背景下，粒子根据运动模型进行传播，然后根据观察结果的可能性对它们进行加权，在重新采样的步骤中，新粒子的绘制概率与观察到的可能性成正比 --》从存储成本和对不断变化的信号特性的快速适应的角度来看，可以实现数据到达时进行实时处理 --》用于对非线性