由掺杂剂波动引起的阈值变化的蒙特卡罗建模

摘要

本文介绍了一种新的 3-D 蒙特卡罗方法，用于模拟 MOSFET 中的随机掺杂剂波动效应。 该方法考虑了器件中的每个硅原子，并且通常适用于任意不均匀的掺杂分布。 除体掺杂波动外，首次研究了源漏掺杂波动对短沟道阈值电压的影响。 结果清楚地表明了逆行体掺杂和浅/突变源漏结的好处。 它还量化了优化设计的 25 nm MOSFET 中由于离散掺杂剂波动引起的阈值电压变化幅度。

介绍

MOSFET 阈值电压 (V) 变化由于掺杂原子的数量和位置的随机变化而成为一个越来越重要的问题，因为器件尺寸缩小并受到越来越多的关注[1-41，之前离散掺杂剂波动的 3D 建模已由 要么为一定数量的掺杂剂随机生成 x、y 和 z 坐标 [11]，要么通过从每个网格 nodet2.31 的泊松分布中随机选择一定数量的掺杂剂。 一般来说，这些技术都使用了均匀的网格和均匀的掺杂分布。

建模技术

在目前的工作中，使用了一种从根本上更精确的方法：识别被模拟器件中的每个硅原子位置，并滚动一个随机数来确定它是否是掺杂剂。 该技术基于以下观察：深亚微米器件中的硅原子总数实际上是相当可控的。 例如，一个 (100 nm)’ 体积（例如可用于模拟非常小的设备）仅包含大约 50x10’ 原子。 50M 随机数可以在比 IV 曲线的 3D 模拟所需的更少的计算机时间内轻松生成。

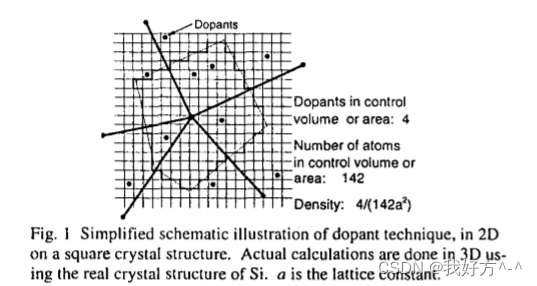
该技术允许使用通用有限元网格模拟任意非均匀掺杂分布。 该过程在图 1 中以 2D 形式说明了一个简单的方形晶体结构，尽管实际计算是在真实 Si 晶格上以 3D 形式完成的。 在任何特定原子位置找到掺杂剂的概率为 N,v 其中 N,r 是局部掺杂剂浓度，11 是与每个原子相关的体积（对于 Si，17 = n.:,/8 = 0.020022 nm’ ）。 当该概率超过该位置的随机数时，将在此处放置掺杂剂，并与有限元网格的最近节点相关联，这与通过有限元方法求解泊松方程所使用的基本假设保持一致。 在找到与每个节点相关的供体和受体原子的总数后，通过除以最接近给定节点的原子位点的总体积，将它们归一化回浓度。

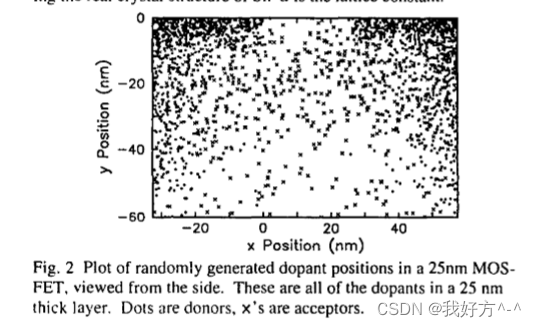
图 2 显示了使用该算法对 25 nm nMOSFET 设计进行定位的掺杂剂示例。 0.225 x 0.2 x 0.1 pm 的模拟体积包含 224550104 个 Si 原子位置，其中 62280 个转化为供体，12703 个转化为受体。 使用这种技术，已经评估了许多不同的 25 nm 沟道长度 MOSFET 设计的阈值电压波动。 所有这些器件的模拟宽度均为 50 nm。 亚阈值状态下的电流是通过使用 FIELDAY[5] 和恒定流动性模型的 3D 扩散模拟计算的，其方式与以前的工作人员 [11.

仿真结果

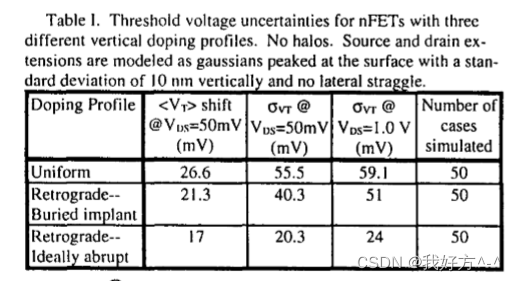
表 I 显示了图 3 中所示的三种不同垂直掺杂分布的结果，从中可以看出极端逆行情况的 V- 波动量最小，而均匀掺杂情况最差。 这是意料之中的，因为极端逆向情况使掺杂剂波动尽可能远离沟道，导致沟道中的潜在变化较小。 也许更令人感兴趣的是 DIBL 与连续到随机平均 V-r 偏移之间的相关性测试，如图 4 所示，用于各种不同的掺杂设计，有些带有晕圈，有些没有，都限制在基本相同的 V .,… 虽然数据确实显示了一些相关性，例如以前的工作人员[3,4] 所建议的，但这种转变总是负面的，即使对于小的 DIBL，这与之前关于正向和负向转变的报道不同[3,4 ]。

图 2 表明，源极和漏极中的掺杂剂波动也可能导致阈值变化，这是以前没有分析过的。 我们已经用逆行 V.r 植入物和晕圈评估了这种效应的“真实”掺杂曲线，这些晕圈设计用于通过分别离散施主或受主同时保持另一个连续掺杂来保持可接受的 V-滚降 [6]。 如图所示。 如图 5 和 6 所示，源极/漏极掺杂确实有助于 V.r 波动，但除了最深的结外，对总变化的影响可以忽略不计。 V., 变化的主要来源是体掺杂，这取决于源/漏掺杂深度，因为它必须随着结深度的增加而增加，以保持恒定的 V.,。 显然，源极和漏极分布的大范围扩展导致阈值电压变化显着增加。

我们得出结论，发现具有合理设计的掺杂分布的 25 nm 沟道长度 MOSFET 的固有阈值电压不确定性约为 1o/fi mVpn”’，其中 W 是 FET 的宽度。 这对于逻辑来说可能是可以容忍的，因为它往往更宽且密度更低，但对于 SRAM 来说可能是有问题的，因为 SRAM 的宽度通常被最小化，芯片上的最大变化可能达到 60，这可能超过 250mV。