java蒙特卡罗求主元素_0049算法笔记——【随机化算法】蒙特卡罗算法,主元素问题,素数测试问题...

2023-11-04 07:59
文章标签 java 算法 随机化 问题 元素 笔记 测试 素数 蒙特卡罗 0049 求主

本文主要是介绍java蒙特卡罗求主元素_0049算法笔记——【随机化算法】蒙特卡罗算法,主元素问题,素数测试问题...，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、蒙特卡罗算法

基本概述

蒙特卡罗(Monte Carlo)方法，又称随机抽样或统计试验方法。传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。

在实际应用中常会遇到一些问题，不论采用确定性算法或随机化算法都无法保证每次都能得到正确的解答。蒙特卡罗算法则在一般情况下可以保证对问题的所有实例都以高概率给出正确解，但是通常无法判定一个具体解是否正确。

设p是一个实数，且1/2

如果对于同一实例，蒙特卡罗算法不会给出2个不同的正确解答，则称该蒙特卡罗算法是一致的。

有些蒙特卡罗算法除了具有描述问题实例的输入参数外，还具有描述错误解可接受概率的参数。这类算法的计算时间复杂性通常由问题的实例规模以及错误解可接受概率的函数来描述。

原理思想

当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

主要步骤

蒙特卡罗解题归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。

1)构造或描述概率过程： 对于本身就具有随机性质的问题，如粒子输运问题，主要是正确描述和模拟这个概率过程，对于本来不是随机性质的确定性问题，比如计算定积分，就必须事先构造一个人为的概率过程，它的某些参量正好是所要求问题的解。即要将不具有随机性质的问题转化为随机性质的问题。

2)实现从已知概率分布抽样： 构造了概率模型以后，由于各种概率模型都可以看作是由各种各样的概率分布构成的，因此产生已知概率分布的随机变量(或随机向量)，就成为实现蒙特卡罗方法模拟实验的基本手段，这也是蒙特卡罗方法被称为随机抽样的原因。最简单、最基本、最重要的一个概率分布是(0,1)上的均匀分布(或称矩形分布)。随机数就是具有这种均匀分布的随机变量。随机数序列就是具有这种分布的总体的一个简单子样，也就是一个具有这种分布的相互独立的随机变数序列。产生随机数的问题，就是从这个分布的抽样问题。在计算机上，可以用物理方法产生随机数，但价格昂贵，不能重复，使用不便。另一种方法是用数学递推公式产生。这样产生的序列，与真正的随机数序列不同，所以称为伪随机数，或伪随机数序列。不过，经过多种统计检验表明，它与真正的随机数，或随机数序列具有相近的性质，因此可把它作为真正的随机数来使用。由已知分布随机抽样有各种方法，与从(0,1)上均匀分布抽样不同，这些方法都是借助于随机序列来实现的，也就是说，都是以产生随机数为前提的。由此可见，随机数是我们实现蒙特卡罗模拟的基本工具。 建立各种估计量： 一般说来，构造了概率模型并能从中抽样后，即实现模拟实验后，我们就要确定一个随机变量，作为所要求的问题的解，我们称它为无偏估计。

3)建立各种估计量：相当于对模拟实验的结果进行考察和登记，从中得到问题的解。 例如：检验产品的正品率问题，我们可以用1表示正品，0表示次品，于是对每个产品检验可以定义如下的随机变数Ti，作为正品率的估计量： 于是，在N次实验后，正品个数为： 显然，正品率p为： 不难看出，Ti为无偏估计。当然，还可以引入其它类型的估计，如最大似然估计，渐进有偏估计等。但是，在蒙特卡罗计算中，使用最多的是无偏估计。 用比较抽象的概率语言描述蒙特卡罗方法解题的手续如下：构造一个概率空间(W ,A,P)，其中，W 是一个事件集合，A是集合W 的子集的s 体，P是在A上建立的某个概率测度；在这个概率空间中，选取一个随机变量q (w ),w Î W ,使得这个随机变量的期望值 正好是所要求的解Q ，然后用q (w )的简单子样的算术平均值作为Q 的近似值。

2、主元素问题

问题描述

设T[1:n]是一个含有n个元素的数组。当|{i|T[i]=x}|>n/2时，称元素x是数组T的主元素。例如：数组T[]={5,5,5,5,5,5,1,3,4,6}中，元素T[0:5]为数组T[]的主元素。

问题求解

算法随机选择数组元素x,由于数组T的非主元素个数小于n/2，所以，x不为主元素的概率小于1/2。因此判定数组T的主元素存在性的算法是一个偏真1/2正确的算法。50%的错误概率是不可容忍的，利用重复调用技术将错误概率降低到任何可接受的范围内。对于任何给定的

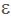de14a7abf1f945eb7cdd4c9fed305080.png>0，算法majorityMC重复调用

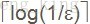c4f114386559d26e4f0c098a696f5dac.png次算法majority。它是一个偏真蒙特卡罗算法，且其错误概率小于

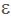de14a7abf1f945eb7cdd4c9fed305080.png。算法majorityMC所需的计算时间显然是

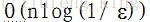3625b6281bea02999701f5fbd8d2d0a3.png。

算法具体代码如下：

//随机化算法 蒙特卡罗算法 主元素问题

#include "stdafx.h"

#include "RandomNumber.h"

#include

#include

using namespace std;

//判定主元素的蒙特卡罗算法

template

bool Majority(Type *T,int n)

{

RandomNumber rnd;

int i = rnd.Random(n);

Type x = T[i];//随机选择数组元素

int k = 0;

for(int j=0; j

{

if(T[j] == x)

{

k++;

}

}

return (k>n/2);//k>n/2时，T含有主元素

}

//重复k次调用算法Majority

template

bool MajorityMC(Type *T,int n,double e)

{

int k = ceil(log(1/e)/log((float)2));

for(int i=1; i<=k; i++)

{

if(Majority(T,n))

{

return true;

}

}

return false;

}

int main()

{

int n = 10;

float e = 0.001;

int a[] = {5,5,5,5,5,5,1,3,4,6};

cout<

for(int i=0; i<10; i++)

{

cout<

}

cout<

cout<

}

程序运行结果如图：

3f14560475e5995afd2fc251678e9e24.png

3、素数测试问题

数学原理

Wilson定理：对于给定的正整数n，判定n是一个素数的充要条件是(n-1)!

00be8f2f6b8ab22ce904d4bd39df29d7.png -1(mod n)。

费尔马小定理：如果p是一个素数，且0

这篇关于java蒙特卡罗求主元素_0049算法笔记——【随机化算法】蒙特卡罗算法,主元素问题,素数测试问题...的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/344374。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
Spring Security 基于表达式的权限控制

Spring Security 基于表达式的权限控制

前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
阅读更多...
浅析Spring Security认证过程

浅析Spring Security认证过程

类图 为了方便理解Spring Security认证流程，特意画了如下的类图，包含相关的核心认证类 概述 核心验证器 AuthenticationManager 该对象提供了认证方法的入口，接收一个Authentiaton对象作为参数; public interface AuthenticationManager {Authentication authenticate(Authenti
阅读更多...
Spring Security--Architecture Overview

Spring Security--Architecture Overview

1 核心组件 这一节主要介绍一些在Spring Security中常见且核心的Java类，它们之间的依赖，构建起了整个框架。想要理解整个架构，最起码得对这些类眼熟。 1.1 SecurityContextHolder SecurityContextHolder用于存储安全上下文（security context）的信息。当前操作的用户是谁，该用户是否已经被认证，他拥有哪些角色权限…这些都被保
阅读更多...
Spring Security基于数据库验证流程详解

Spring Security基于数据库验证流程详解

Spring Security 校验流程图 相关解释说明（认真看哦） AbstractAuthenticationProcessingFilter 抽象类 /*** 调用 #requiresAuthentication(HttpServletRequest, HttpServletResponse) 决定是否需要进行验证操作。* 如果需要验证，则会调用 #attemptAuthentica
阅读更多...
Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
Java架构师知识体认识

Java架构师知识体认识

源码分析 常用设计模式 Proxy代理模式Factory工厂模式Singleton单例模式Delegate委派模式Strategy策略模式Prototype原型模式Template模板模式 Spring5 beans 接口实例化代理Bean操作 Context Ioc容器设计原理及高级特性Aop设计原理Factorybean与Beanfactory Transaction 声明式事物
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
性能测试介绍

性能测试介绍

性能测试是一种测试方法，旨在评估系统、应用程序或组件在现实场景中的性能表现和可靠性。它通常用于衡量系统在不同负载条件下的响应时间、吞吐量、资源利用率、稳定性和可扩展性等关键指标。 为什么要进行性能测试 通过性能测试，可以确定系统是否能够满足预期的性能要求，找出性能瓶颈和潜在的问题，并进行优化和调整。 发现性能瓶颈：性能测试可以帮助发现系统的性能瓶颈，即系统在高负载或高并发情况下可能出现的问题
阅读更多...
Java进阶13讲__第12讲_1/2

Java进阶13讲__第12讲_1/2

多线程、线程池 1.  线程概念 1.1  什么是线程 1.2  线程的好处 2.   创建线程的三种方式 注意事项 2.1  继承Thread类 2.1.1 认识  2.1.2  编码实现  package cn.hdc.oop10.Thread;import org.slf4j.Logger;import org.slf4j.LoggerFactory
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2