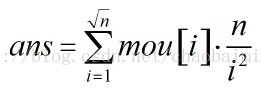莫比专题
hdu6053 TrickGCD 莫比乌斯反演
TrickGCD Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others) Problem Description You are given an array A , and Zhu wants to know there are how many d
学习笔记 ---- 莫比乌斯反演总结
文章目录 概述前置知识数论分块狄利克雷卷积积性函数 莫比乌斯函数定义性质 莫比乌斯反演因子形式倍数形式 例题周期性字符串互质数对[NOI2010D1T1]能量采集BZOJ2820 YY的GCD[SDOI2015] 约数个数和BZOJ4407 于神之怒加强版【BZOJ2693】jzptab最小公倍数之和[bzoj3529-Sdoi2014] 数表 练习题51nod 1675 序列变换BZOJ3
BZOJ 2440 2301 莫比乌斯应用
http://www.lydsy.com/JudgeOnline/problem.php?id=2440 Description 小 X 自幼就很喜欢数。但奇怪的是,他十分讨厌完全平方数。他觉得这些 数看起来很令人难受。由此,他也讨厌所有是完全平方数的正整数倍的数。然而 这丝毫不影响他对其他数的热爱。 这天是小X的生日,小 W 想送一个数给他作为生日礼物。当然他不能送一 个小X讨厌
莫比乌斯反演 两种形式
莫比乌斯反演在数论中占有重要的地位,许多情况下能大大简化运算。那么我们先来认识莫比乌斯反演公式。 定理:和是定义在非负整数集合上的两个函数,并且满足条件,那么我们得到结论 在上面的公式中有一个函数,它的定义如下: (1)若,那么 (2)若,均为互异素数,那么 (3)其它情况下 对于函数
CodeForces 547C. Mike and Foam 莫比乌斯反演
题意:给定一个长度为n的数列a,和q个操作(1<= n,q <= 2*10^5, 1 <= a[i] <= 5*10^5 ) 需要维护一个多重集合Q. 每个操作给出一个下标i,如果a[i]属于Q那么把a[i]从Q中拿走,如果a[i]不属于Q,那么把a[i]加入Q中。 每次操作后询问Q中,有多少对i,j满足条件 i<j 且 gcd(a[i],a[j])=1 这个性质的维护比较困难,直
HDU 1695 GCD 容斥原理/莫比乌斯反演
题意: 给你两个区间[a,b],[c,d],还有一个k。让你从区间[a,b]中找出x,[c,d]中找出y,问共有多少组(x,y)使得gcd(x,y)=k。 (x,y)和(y,x)算一组。 思路: 参考:http://blog.csdn.net/yang_7_46/article/details/9072533 容斥。 普通容斥: *如果gcd(x,y)=k,则gcd(x/k
SPOJ 7001 Visible Lattice Points(莫比乌斯反演)
莫比乌斯反演,注意0的情况特殊考虑下就可以了 #include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int N = 1000005;int mo[N], prime[N], pn;bool vis[N];void Moblus() {memset(vis, false, siz
组合数学常用内容——基础内容+莫比乌斯反演
组合数学常用公式 A(n,r)=n(n-1)…(n-r+1)=n!/(n-r)!C(n,r)=A(n,r)/r!=n!/((n-r)r!)C(n,r)=C(n,n-r)C(n,r)=C(n-1,r)+C(n-1,r-1)C(n+r+1,r)=C(n+r,r)+C(n+r-1,r-1)+…+C(n+1,1)+C(n,0)C(n,k)C(k,r)=C(n,r)C(n-r,k-r)C(n,k+1)=C
Hillan and the girl —— 莫比乌斯对两个累加的优化
Problem Description “WTF! While everyone has his girl(gay) friend, I only have my keyboard!” Tired of watching others’ affair, Hillan burst into scream, which made him decide not to hold it back. “A
bzoj2005 [NOI2010]能量采集 莫比乌斯反演
题目链接:传送门 考虑点 ( x , y ) (x,y) (x,y)对答案的贡献: 设 g c d ( x , y ) = k gcd(x,y)=k gcd(x,y)=k, x = a k , y = b k . x=ak,y=bk. x=ak,y=bk. 若有 x ′ , y ′ x',y' x′,y′满足 ( x ′ , y ′ ) (x',y') (
three.js实现的莫比乌丝圈
three.js实现的莫比乌丝圈 标题 <!DOCTYPE html> <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title>three.js 实现的莫比乌丝圈</title> <style type="text/css"> body
BZOJ 2301 [HAOI2011]Problem b (容斥+莫比乌斯反演+分块优化 详解)
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MB Submit: 2096 Solved: 909 [Submit][Status][Discuss] Description 对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd(x,y
UESTC 618 无平方因子数 (容斥 + 莫比乌斯反演)
无平方因子数 Time Limit: 4000/2000MS (Java/Others) Memory Limit: 65535/65535KB (Java/Others) Submit Status 无平方因子数即对于任意一个素数p,p2都不会整除那个数,如1 , 5=5 , 15=3×5都是无平方因子数,而20=22×5不是。现在给定一个n (1≤n<1012)
BZOJ 2440 完全平方数 (容斥+莫比乌斯反演+二分)
2440: [中山市选2011]完全平方数 Time Limit: 10 Sec Memory Limit: 128 MB Submit: 1673 Solved: 799 [ Submit][ Status][ Discuss] Description 小 X 自幼就很喜欢数。但奇怪的是,他十分讨厌完全平方数。他觉得这些 数看起来很令人难受。由此,他也讨厌所有是完
NOJ 2079 Prime (莫比乌斯反演)
Prime 时间限制(普通/Java):1000MS/3000MS 运行内存限制:65536KByte 总提交:267 测试通过:11 比赛描述 给定n个数,求两两互斥的对数。互斥是指两个数的最大公约数是1 输入 第一行为样例数T(T<=5) 对每个样例,第一行为一个整数n(2=<n<=10^5),代表数的个数。 接下来一行包含n个数,a1,a2
NJUST 1923 triple (莫比乌斯反演)
triple Time Limit: 3000MS Memory Limit: 65536KB Description 给出一个整数n,表示1,2,...,n。从这n个数中任意选择3个不同的数字x,y,z,问x,y,z的最大公约数等于m的方案有多少种?(注意:(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)属于同一种方案)
P9238 [蓝桥杯 2023 省 A] 翻转硬币(杜教筛+莫比乌斯)
题目:https://www.luogu.com.cn/problem/P9238 思路: 代码: #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<string> #include<cstring> #include<cmath> #include<ctime> #include<algorithm> #include<
P3768 简单的数学题(莫比乌斯反演+杜教筛)
题目:P3768 简单的数学题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路: 代码: #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<string> #include<cstring> #include<cmath> #include<ctime> #include<algorithm>
BZOJ2440(完全平方数)二分+莫比乌斯容斥
题意:完全平方数是指含有平方数因子的数。求第ki个非完全平方数。 解法:比较明显的二分,getsum(int middle)求1-middle有多少个非完全平方数,然后二分。求1-middle的非完全平方数个数可以用总数减掉完全平方数个数。计算完全平方数的个数用容斥: 首先加上n/(2*2)+n/(3*3)+n/(5*5)+n/(7*7)...+...然后减掉出现两次的
莫比乌斯函数求和公式理解
就是对这个公式的理解 ∑i=1n∑d|iu(d)=1 ∑ i = 1 n ∑ d | i u ( d ) = 1 \sum_{i=1}^n\sum_{d|i}u(d) = 1 首先 ∑d|iu(d)=0,i不等于1的时候 ∑ d | i u ( d ) = 0 , i 不 等 于 1 的 时 候 \sum_{d|i}u(d) = 0,i不等于1的时候
bzoj 2301 [HAOI2011]Problem b(莫比乌斯反演)
https://www.lydsy.com/JudgeOnline/problem.php?id=2301 这道题阔以作为模板莫比乌斯的模板 并且代码里的函数的意义也与标准的相同: f(d,n,m) f ( d , n , m ) f(d,n,m) 代表小于等于 n、m n 、 m n、m 的 gcd(x,y)=d g c d ( x , y ) = d gcd(x,y)=d 的
hdu 4746 Mophues (莫比乌斯反演)
第二个样例: N=10,M=10,P=1 N = 10 , M = 10 , P = 1 N=10,M=10,P=1 ans=f(1)+f(2)+f(3)+f(5)+f(7) a n s = f ( 1 ) + f ( 2 ) + f ( 3 ) + f ( 5 ) + f ( 7 ) ans=f(1)+f(2)+f(3)+f(5)+f(7) 每个 f f f 具体的值 以 F
sopj 7001 (莫比乌斯反演)
https://vjudge.net/contest/238531#problem/B 题意:给一个 N×N×N N × N × N N\times N\times N的坐标系,从源点 (0,0,0)发出的光线,最多能照到几个坐标点 这道题用的是莫比乌斯反演的倍数那种形式 也就是 F(n)=∑n|df(d) F ( n ) = ∑ n | d f ( d ) F(n)=\s
Python 科技研究之 01 在 Python 中可视化莫比乌斯带
在 Python 中可视化莫比乌斯带 查看全文http://www.taodudu.cc/news/show-8467391.html相关文章:莫比乌斯反演(二):莫比乌斯函数c语言编程题 共40题,C语言编程题 经典40题附解答.pptc语言案例程序设计,以程序案例为导向的《C语言程序设计》的教学研究2021-09-03用集合写一个简单的
【bzoj3529】【SDOI2014】【数表】【莫比乌斯反演+树状数组】
Description 有一张N×m的数表,其第i行第j列(1 < =i < =礼,1 < =j < =m)的数值为 能同时整除i和j的所有自然数之和。给定a,计算数表中不大于a的数之和。 Input 输入包含多组数据。 输入的第一行一个整数Q表示测试点内的数据组数,接下来Q行,每行三个整数n,m,a(|a| < =10^9)描述一组数据。 Output 对每组数据,输出一行一个整数





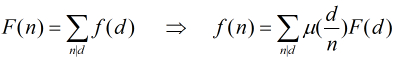
![P9238 [蓝桥杯 2023 省 A] 翻转硬币(杜教筛+莫比乌斯)](https://img-blog.csdnimg.cn/direct/28382e30730a4b44ab3f4238e1866d6d.jpeg)