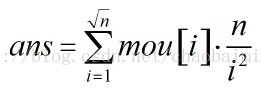BZOJ2440(完全平方数)二分+莫比乌斯容斥

本文主要是介绍BZOJ2440(完全平方数)二分+莫比乌斯容斥，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意：完全平方数是指含有平方数因子的数。求第ki个非完全平方数。

解法：比较明显的二分，getsum(int middle)求1-middle有多少个非完全平方数，然后二分。求1-middle的非完全平方数个数可以用总数减掉完全平方数个数。计算完全平方数的个数用容斥：

首先加上n/(2*2)+n/(3*3)+n/(5*5)+n/(7*7)...+...然后减掉出现两次的，然后加上三次的...奇加偶减。这就是mou的原型，用mou数组计算很简单；

代码：


/******************************************************
* @author:xiefubao
*******************************************************/
#pragma comment(linker, "/STACK:102400000,102400000")
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
#include <set>
#include <stack>
#include <string.h>
//freopen ("in.txt" , "r" , stdin);
using namespace std;
 
#define eps 1e-8
#define zero(_) (abs(_)<=eps)
const double pi=acos(-1.0);
typedef unsigned long long LL;
const int Max=100010;
const LL INF=2e16+7;
 
LL mou[Max];
void init()
{
    for(LL i=2; i<Max; i++)
{
        if(!mou[i])
{
mou[i]=i;
            for(LL j=i*i; j<Max; j+=i)
mou[j]=i;
}
}
mou[1]=1;
    for(int i=2; i<Max; i++)
{
        if(i/mou[i]%mou[i]==0) mou[i]=0;
        else mou[i]=-mou[i/mou[i]];
}
}
int k;
LL getnum(LL middle)
{
LL ans=0;
    for(LL i=1; i*i<=middle; i++)
{
ans+=mou[i]*(middle/(i*i));
}
    return ans;
}
int main()
{
init();
    int t;
    cin>>t;
    while(t--)
{
        scanf("%d",&k);
LL left=1,right=INF;
        while(left<=right)
{
            int middle=(left+right)/2;
            if(getnum(middle)<k)
left=middle+1;
            else
right=middle-1;
}
        cout<<left<<'\n';
}
    return 0;
}