结论专题
7 个有效策略,让撰写论文结论部分更轻松,留下深刻印象又有影响力
写出有效的结论对于任何论文的成功都至关重要。这是您给读者留下持久印象并阐明您的要点的最后机会。一个精心设计的结论可以将你的文章从优秀提升到卓越,使其令人难忘和有影响力。让我们探索七种强大的策略,以创建引人注目的论文结论,从而引起您的听众的共鸣。 1. 呼应你的开场白 结束你的文章的一种有效技巧是通过重新审视关键图像、故事或想法来与你的引言产生共鸣。这种方法提供了一种完成感,同时展示了你的论点在
数三角形(二)》-筛除法斜线结论
算法思路: 1、一个直观的思路是筛除法,即:答案=总数-三点共线的种数 总数易求得,为组合数C((n+1)*(m+1),3),考虑到n、m数值范围,考虑用long long。 2、三点共线的情况有: (1)网格顶点同行,每行有m+1个顶点,共n+1行,共有:C(m+1,3) * (n+1) (2)网格顶点同列,每列有n+1个顶点,共m+1列,共有:C(n+1,3) * (m+1) (3)网格顶
结论:java 中不存在真正的引用传递,引用传递也是传递的地址值
解释的很清楚,做个备份。 https://blog.csdn.net/suifeng629/article/details/83576917
关于Mybatis的Batch模式性能测试及结论
近日在公司项目中,使用到spring+mybatis的架构,特对mybatis的batch模式做了相关研究,得出以下结论: 1.Mybatis内置的ExecutorType有3种,默认的是simple,该模式下它为每个语句的执行创建一个新的预处理语句,单条提交sql;而batch模式重复使用已经预处理的语句, 并且批量执行所有更新语句,显然batch性能将更优; 2.但batch模
现代数字信号处理及其应用-常见结论
现代数字信号处理及其应用-常见结论 本文的结论均摘抄自 何子述、夏威等编著,《现代数字信号处理及其应用》,清华出版社出版。 解析信号=信号预包络;基带信号=信号复包络。BT法(自相关谱估计法):间接法,先求自相关函数(有偏估计和无偏估计)[p-77],再做fft得到功率谱估计。有偏估计的均值有一个三角窗,但是方差是渐进一致估计。无偏估计的均值为0,但是方差大于有偏估计,当采样点远大于m的时候,
小程序干掉APP这个结论或许下的太早 但小程序有许多可取之处
任何一个伟大的产品的诞生,需要具备两个特点,继承和颠覆。就拿微信小程序来说,和APP比较,一方面继承了APP很多特点,另一方面,对于移动这一产品来说,有可能会颠覆。 张小龙曾表示:“一个好的产品应该是让用户用完即走的,不应该黏住用户。任何产品都只是一个工具,对工具来说,好的工具就是应该最高效率的完成用户的目的,然后尽快的离开。” 作为不知名企业,我们可以虚拟一下
同一工程中不同RS的问题结论
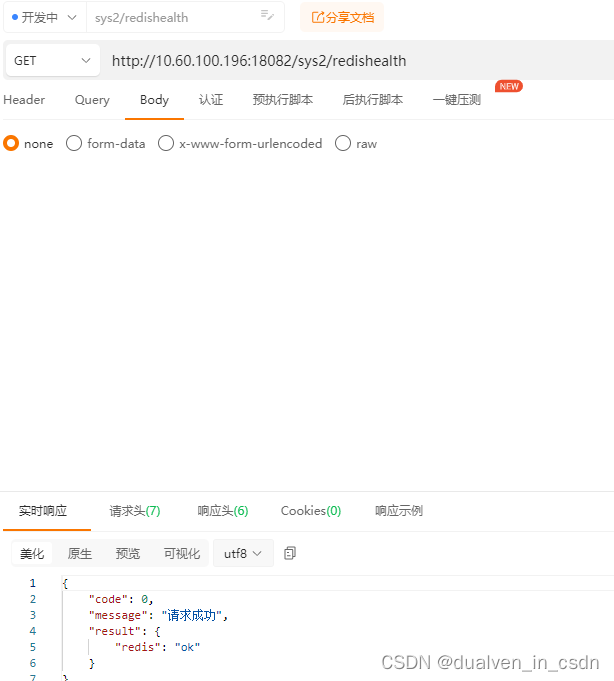
目录 MeshDevice/deviceAll && /wvp/device 编辑 故意改成mesh下的RS,结果包裹了: sys2/redishealth 编辑 编辑 原因解析 MeshDevice/deviceAll && /wvp/device 测试结果:都使用 import com.gbcom.wvp.domain.vo.RS; 返回结果就没有多余
数学分析复习: 连续函数、可微函数的重要结论梳理
文章目录 连续函数、可微函数的重要结论梳理总结细节1.有界性定理2.最值定理3.介值定理4.中值定理5.洛必达法则6.泰勒公式 本篇文章适合个人复习翻阅,不建议新手入门使用 连续函数、可微函数的重要结论梳理 总结 在数学分析一中,关于闭区间上的连续函数,我们用区间套公理可获得一系列结论 区间套定理 ⇒ \Rightarrow ⇒ 有界性定理 ⇒ \Righta
组合数学中的几个结论
1. 鸽巢原理 :把 n+1 个物体放入n个盒子中,必有一个盒子包含两个或更多的物品2. n元集合的r圆排列数为p(n,r)/r;3.从(0,0)点沿水平和垂直道路可以走到(m,n)点,方法有c(m+n,m)种4.多重集合M={a1,a2,a3,...,ak}的r组合数为c(k+r-1,r)5.正整数n的有序k分拆的个数为c(n-1,k-1)6.n的无序k分拆数为B(n,k),满足B(n+
J - Juggling Troupe Gym - 101623J(结论)
题意: 一些数(0,1,2)。 每轮游戏中2会分到左右两个位置(第一个和最后一个只会分到一个位置)。 全是0,1时游戏结束,求最终序列。 思路: 感觉像个经典结论题(波形碰撞?),但是找不到源头,感觉证明不了。。。 将每个2单独考虑,找到其左边第一个a[l]=0,右边第一个a[r]=0,可以发现在l+r-x的位置会出现0,a[l],a[r]变成1。然后依次考虑下去。 #include<cstd
Codeforces 1459 Row GCD(GCD,结论)
You are given two positive integer sequences 𝑎1,…,𝑎𝑛 and 𝑏1,…,𝑏𝑚. For each 𝑗=1,…,𝑚 find the greatest common divisor of 𝑎1+𝑏𝑗,…,𝑎𝑛+𝑏𝑗. Input The first line contains two integers 𝑛 and
详解GPT-1到GPT-3的论文亮点以及实验结论
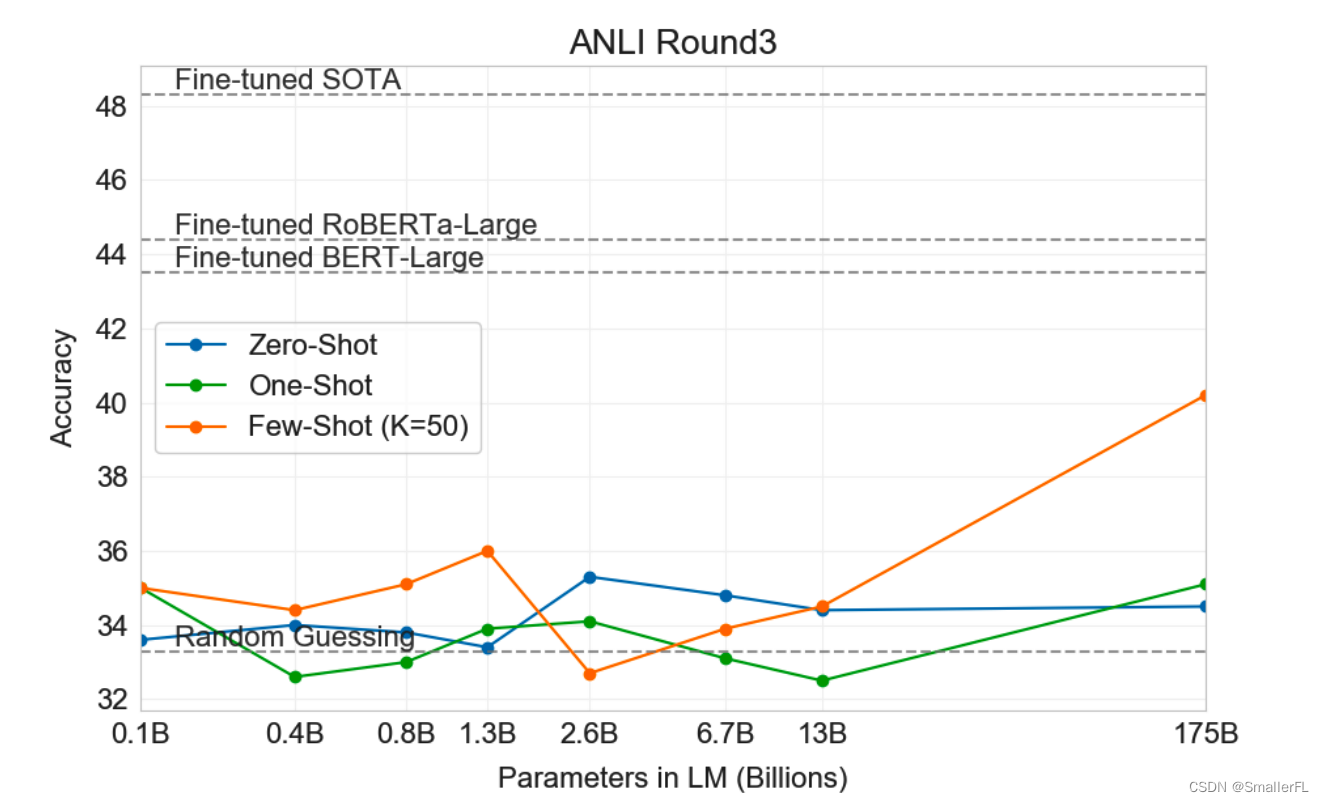
文章目录 1. 前言2. GPT-12.1 亮点2.2 实验结论 3. GPT-23.1 亮点3.2 实验结论 4. GPT-34.1 亮点4.2 实验结论 5. 总结6. 参考 1. 前言 Generative Pre-trained Transformer 即 GPT。这篇文章结合论文总结一些 GPT-1 到 GPT-4 的架构和性能上的差异。GPT 系列是由 OpenA
汉明码检错与纠错的结论(hamming code)
假如一组二进制数据为101,另外一组为111,那么显然把第一组的第二位数据0改成1就可以变成第二组数据111,所以两组数据的汉明距离就为1 简单点说,汉明距离就是一组二进制数据变成另一组数据所需的步骤数(它表示两个相同长度的字符串对应位置的不同字符的数量),显然,这个数值可以衡量两张图片的差异,汉明距离越小,则代表相似度越高。汉明距离为0,即代表两张图片完全一样。
BZOJ 1121 [POI2008]激光发射器SZK 结论题
Description 多边形相邻边垂直,边长为整数,边平行坐标轴。要在多边形的点上放一些激光发射器和接收器。满足下列要求: 1发射器和接收器不能放置在同一点; 2发射器发出激光可以沿壁反射,最终到达一个接收器; 3发射器只能沿角平分线发射激光。求:最多可放置多少对发射器和接收器?点数4<=n<=100000 Input 第一行给出一个数字N,代表有多少个点. 下面N行,用来描述点的
您之个人命运形势分析和理性解法结论:匆忙之间做出的选择,确实容易出错
就是一个事情,就是您看书那么多,为啥自己过的这么不如意呢? 就是本身没把自己的日子过好, 其他说啥子道理,都是瞎摆活,不是吗? 学的知识没用到个人身上来。至于儒释道是,不错,是很好的。但是一时之间根本无法达到,或者说修行到最高的一层去了。虽然心里面想着这个事情。但是近在眼前的事情,需要先处理好啊。 否则生存,活都问题了,还说啥子修行? 都是空话而已。 而且您目前
Meta分析:如何为生态环境领域提供可靠结论
Meta分析,又称元分析,是一种统计方法,用于整合多个独立研究的结果,从而得出更为全面、可靠的结论。在生态领域,Meta分析发挥着越来越重要的作用,它有助于解决单个研究样本量小、结果不一致等问题,从而更准确地揭示生态现象和规律。 在生态学中,Meta分析的应用范围广泛,涵盖了生物多样性、种群动态、生态系统服务等多个方面。通过整合大量研究数据,Meta分析能够评估不同因素对生态系统的影响的大小和方
我爬了《流浪地球》十万个短评得出以下结论
前言 最近大家讨论最多的就是《流浪地球》了,偶尔刷逼乎,狗血的事情也是层出不穷,各种撕逼大战,有兴趣的小伙伴可以自行搜索。 截止目前,《流浪地球》已上映20天,累计票房43.94亿,豆瓣评分7.9分。博主是正月初七看的,票价有点小贵,整体效果还算可以,虽然剧情有点尴尬,各种镜头切换有时候看的稀里糊涂,但还是给了豆瓣四星好评。 爬取 逼乎上很多高手,对《流浪地球》在豆瓣的评分做了细思缜密的分析,
(8-5-6)制作美股交易策略模型:投资组合模拟+可视化+结论
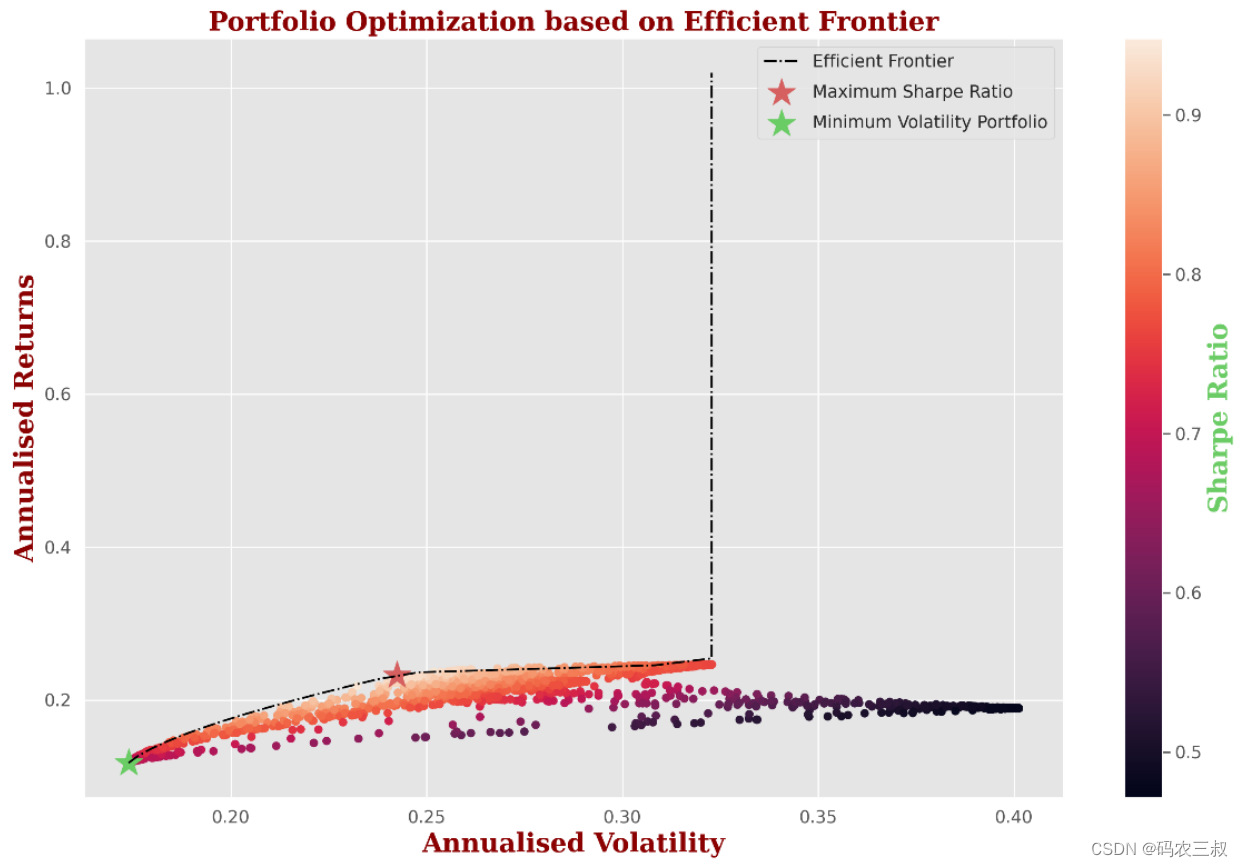
8.5.8 投资组合模拟 在本项目中,使用Google、Apple、Facebook、Amazon以及S&P 500市场指数进行投资组合模拟,本项目使用了Python的Scipy.optimize包实现模拟功能。通过调整资产配置,我们将生成2673个投资组合。在本模拟中考虑了历史收益、波动性和相关性,以构建有效的投资组合。在0%的无风险利率下,我们将评估这些投资组合相对于无风险投资的表现。本项
11.频域里的卷积——傅里叶变换的性质,傅里叶对,结论_3
目录 傅里叶变换的性质 傅里叶对 总结 傅里叶变换的性质 让我们继续看看空间域和频域之间的关系。这是傅里叶变换的一些简单性质。我们从一个我们已经讨论过的问题开始。一切都是线性的因为我们只是做求和和乘法(如图),对吧? 我们刚才描述的是这个卷积。空间域的卷积就是频域的乘法,反之亦然, 一个有趣事情的是缩放。所以,如果我用一个常数a来缩放一个函数。我们这样想,假设a大于1,
AtCoder AGC032E Modulo Pairing (二分、贪心结论)
题目链接 https://atcoder.jp/contests/agc032/tasks/agc032_e 题解 猜结论好题。 结论是: 按\(a_i\)从小到大排序之后,一定存在一种最优解,使得以某个位置为界,两边分别首尾匹配,且满足左边的每一对的和都\(<M\), 右边每一对的和都\(\ge M\). 证明不难,可参考官方题解,此处不再赘述。 然后显然可以枚举这个临界点,然后\(O(n)\
结论不重要, 思路才重要------从linux中svn diff失效来谈谈.svn/text-base目录下的.svn-base文件
先说说事情的来龙去脉吧! 由于需要, 我们要批量改动某目录下的打印log的接口, 简单来说, 要把某目录下的所有文件中的api_log_A改为api_log_B . 某同学有过做类似事情的经验, 并且成功了, 于是直接把命令给我, happy啊。 于是乎, 我执行了一下这个命令, 实现了批量替换, 我确认, 确实替换成功了, 但是, 准备提交前,
这个结论很可能是正确的,
下面问题 原题是说,下面的等式 ∫ 0 ∞ ∏ k = 0 N ( sin t 100 k + 1 t 100 k + 1 ) d t = π 2 \int_0^\infty\prod\limits_{k=0}^{N}\left(\dfrac{\sin \dfrac{t}{100k+1}}{\dfrac{t}{100k+1}}\right)dt=\dfrac{\pi}2 ∫0∞k=0∏
关键结论和引用论文记录(比较杂)
1.解非线性薛定谔方程有很多递归解法,分布傅里叶算法是最准确,计算复杂度最低的解法 T. R. Taha and M. J. Ablowitz, “Analytical and numerical aspects of certain nonlinear evolution equation, II, numerical, nonlinear Schroedinger equation,” J.
电容两端电压不能突变结论
只需要记住结论就好了,如果V1电源发生突变,电容的上端接着R1,下端接着GND,所以电容两端的电压不变(指的是两级板各自的电压),然后电容的上极板逐渐充电,电位上抬。 如果GND发生突变,则电容下级板的电压突变,电容两端电压不会突变,则上极板电压也随之突变。 具体实验可以看下面的博文。这里贴出他给的结论。 真实的电路中,电阻是永远存在的,电容两端的充放电难度(例如较为简单的电路情形就是
伪类和伪元素的区别(结论)
首先,阅读 w3c 对两者的定义: CSS 伪类用于向某些选择器添加特殊的效果。CSS 伪元素用于将特殊的效果添加到某些选择器。 可以明确两点,第一两者都与选择器相关,第二就是添加一些“特殊”的效果。这里特殊指的是两者描述了其他 css 无法描述的东西。 伪类种类 伪元素种类 区别 说人话:伪类的效果可以通过添加一个实际的类来达到,而伪元素的效果则需要通过添加






![BZOJ 1121 [POI2008]激光发射器SZK 结论题](http://www.lydsy.com/JudgeOnline/images/1121.jpg)