本文主要是介绍(8-5-6)制作美股交易策略模型:投资组合模拟+可视化+结论,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
8.5.8 投资组合模拟
在本项目中,使用Google、Apple、Facebook、Amazon以及S&P 500市场指数进行投资组合模拟,本项目使用了Python的Scipy.optimize包实现模拟功能。通过调整资产配置,我们将生成2673个投资组合。在本模拟中考虑了历史收益、波动性和相关性,以构建有效的投资组合。在0%的无风险利率下,我们将评估这些投资组合相对于无风险投资的表现。本项目旨在了解多元化的好处和风险降低,为构建与投资者风险承受能力和回报目标相符的良好多元化投资组合提供见解。
(1)下面这段代码是进行投资组合模拟的实现,通过使用SciPy库中的minimize函数。在生成2673个投资组合时,对每个投资组合进行了权重的分配,其中使用了Dirichlet分布。通过计算每个投资组合的预期收益、预期波动性和夏普比率,以及考虑了无风险利率,从而得到投资组合的性能指标。这有助于理解多元化的效果、风险和回报之间的权衡,并提供了构建优化投资组合的信息。
from scipy.optimize import minimize
# Portfolio Simulation
portfolio = 2673 # generation of a portfolio
n_assets = returns.shape[1]
weights = np.random.dirichlet(np.full(n_assets,0.05),portfolio)
mean_returns = returns.mean()
sigma = returns.cov()
expected_returns = np.zeros(portfolio)
expected_vol = np.zeros(portfolio)
sharpe_ratio = np.zeros(portfolio)
rf_rate = 0.0 # risk free ratefor i in range(portfolio):w = weights[i,:]expected_returns[i] = np.sum(mean_returns @ w)*252expected_vol[i] = np.sqrt(np.dot(w.T,sigma @ w))*np.sqrt(252)sharpe_ratio[i] = (expected_returns[i]-rf_rate)/expected_vol[i](2)定义如下所示的三个函数,这三个函数将在后续的投资组合优化中使用。
- portfolio_volatility(weight):用于计算投资组合的波动性,接受权重向量作为参数。
- portfolio_return(weight):用于投资组合的预期收益,同样接受权重向量作为参数。
- portfolio_performance(weight):用于投资组合的收益和波动性,返回一个元组包含两个值,分别是预期收益和波动性。同样,接受权重向量作为参数。
def portfolio_volatility(weight):return np.sqrt(np.dot(weight.T,np.dot(sigma,weight)))*np.sqrt(252)def portfolio_return(weight):return np.sum(mean_returns*weight)*252def portfolio_performance(weight):return_p = portfolio_return(weight)vol_p = portfolio_volatility(weight)return return_p, vol_p(3)下面的这两个函数定义了投资组合优化的目标和优化过程,这两个函数是投资组合优化中关键的部分。
- negativeSR(weight):用于计算投资组合的负夏普比率。在优化时,我们希望最大化夏普比率,但minimize 函数实际上是一个最小化问题,所以我们取负夏普比率进行最小化。函数返回的值是 -(return_p - rf_rate)/vol_p,其中 return_p 是投资组合的预期收益,vol_p 是波动性,rf_rate 是无风险利率。
- max_sharpe_ratio():用于执行实际的优化过程。在内部定义了一个辅助函数 sum_one,用于确保权重总和为1。然后,通过使用 minimize 函数,基于定义的 negativeSR 函数进行夏普比率的最大化。最终max_sharpe_ratio()返回的是最优权重的结果。
def negativeSR(weight):return_p, vol_p = portfolio_performance(weight)rf_rate = 0.025return -(return_p - rf_rate)/vol_pdef max_sharpe_ratio():def sum_one(weight):w= weightreturn np.sum(weight)-1n_assets = returns.shape[1]weight_constraints = ({'type':'eq','fun': sum_one})w0 = np.random.dirichlet(np.full(n_assets,0.05)).tolist() # w0 is an initila guessreturn minimize(negativeSR,w0,method='SLSQP',bounds =((0,1),)*n_assets,constraints = weight_constraints)(4)函数 min_vol()的功能是最小化投资组合波动率。函数使用 minimize 函数,基于定义的 portfolio_volatility 函数,执行投资组合波动率的最小化,并返回最优权重的结果。这个函数在构建有效前沿(Efficient Frontier)时是非常关键的。其中n_assets 是资产数量; weight_constraints 定义了一个等式约束,确保所有权重的总和等于1; w0 是初始权重的猜测; bounds 是权重的边界,确保它们在 [0, 1] 的范围内。
def min_vol():n_assets = returns.shape[1]weight_constraints = ({'type':'eq','fun': lambda x: np.sum(x)-1})w0 = np.random.dirichlet(np.full(n_assets,0.05)).tolist()bounds = ((0,1),)*n_assetsreturn minimize(portfolio_volatility,w0,method='SLSQP',bounds = bounds,constraints = weight_constraints)(5)函数 efficient_portfolio_target(target) 用于找到给定目标收益率下的有效投资组合。以下是对关键信息的说明:
- target 是目标收益率。
- constraints 包括两个等式约束:一个确保投资组合的预期收益率等于目标,另一个确保所有权重的总和等于1。
- w0 是初始权重的猜测。
- bounds 是权重的边界,确保它们在 [0, 1] 的范围内。
def efficient_portfolio_target(target):constraints = ({'type':'eq','fun': lambda x: portfolio_return(x)- target},{'type' :'eq','fun': lambda x: np.sum(x)-1})w0 = np.random.dirichlet(np.full(n_assets,0.05)).tolist()bounds = ((0,1),)*n_assetsreturn minimize(portfolio_volatility,w0, method = 'SLSQP',bounds = bounds,constraints = constraints)在上述代码中,函数使用 minimize 函数,基于定义的 portfolio_volatility 函数,执行在给定目标收益率下最小化投资组合波动率,并返回最优权重的结果。这对于构建有效前沿(Efficient Frontier)和制定风险和收益平衡的投资策略非常有用。
(6)函数 efficient_frontier(return_range) 用于生成在给定一系列目标收益率下的有效投资组合。参数return_range 是一个列表,包含多个目标收益率。函数 efficient_frontier(return_range) 使用列表推导来创建一个由每个目标收益率生成的有效投资组合列表,每个目标收益率都被传递给 efficient_portfolio_target 函数,以找到相应目标下的最优权重。
def efficient_frontier(return_range):return [efficient_portfolio_target(ret) for ret in return_range]通过调用这个函数,可以得到有效前沿上的一组投资组合,每个投资组合都在给定目标收益率下最小化了投资组合的波动率。这有助于投资者在不同风险和收益水平下做出明智的投资决策。
8.5.9 投资组合可视化
(1)下面代码实现了投资组合的优化可视化,通过使用Python中的库Scipy.optimize进行投资组合模拟。通过生成大量权重分配来构建投资组合,考虑历史收益、波动性和相关性,以生成有效投资组合。在考虑风险无息率为0的情况下,通过评估各个投资组合的性能相对于无风险投资,分析了投资组合的多样化效益和风险降低。绘制了投资组合的散点图和有效前沿图,展示了投资组合的风险和收益之间的权衡关系,强调了夏普比率最大和波动率最小的投资组合。这有助于投资者在不同的风险水平下做出明智的投资决策。
sharpe_maximum = max_sharpe_ratio()
return_p,vol_p = portfolio_performance(sharpe_maximum['x'])
min_volatility = min_vol()
return_min,vol_min = portfolio_performance(min_volatility['x'])plt.figure(figsize =(15,10))
plt.style.use('ggplot')
plt.scatter(expected_vol,expected_returns, c = sharpe_ratio)
# plt.colorbar.sel(label = 'Sharpe Ratio',size=20)
plt.colorbar().set_label('Sharpe Ratio', size= 20, color = 'g', family='serif',weight='bold')
target = np.linspace(return_min,1.02,100)
efficient_portfolios = efficient_frontier(target)
plt.plot([i.fun for i in efficient_portfolios], target, linestyle ='dashdot', color ='black',label='Efficient Frontier')
plt.scatter(vol_p,return_p, c = 'r', marker='*', s = 500, label = 'Maximum Sharpe Ratio')
plt.scatter(vol_min,return_min, c = 'g', marker ='*', s = 500, label='Minimum Volatility Portfolio')font1 = {'family':'serif','color':'darkred','size':20,'weight':'bold'}
font2 = {'family':'serif','color':'darkred','size':20,'weight':'bold'}
plt.title('Portfolio Optimization based on Efficient Frontier',fontdict=font1)
plt.xlabel('Annualised Volatility',fontdict=font2)
plt.ylabel('Annualised Returns',fontdict=font2)
plt.legend(labelspacing=0.8)执行后绘制投资组合的散点图和有效前沿,效果如图8-8所示。具体说你如下所示:
- 图中展示了2673个不同权重下的投资组合,其中横轴表示年化波动率,纵轴表示年化收益率,散点的颜色表示夏普比率,越深的颜色表示夏普比率越高。
- 有效前沿(Efficient Frontier)是一条用虚线标识的曲线,表示在给定风险水平下,投资组合可以实现的最大收益。这是通过尝试不同目标收益率来生成的。
- 最大夏普比率的投资组合用红色星星标识,最小波动率的投资组合用绿色星星标识。这两个投资组合代表了夏普比率最大和波动率最小的极端情况。
整体来说,这张图帮助投资者在风险和收益之间找到平衡点,通过选择适当的投资组合权重来实现其投资目标。
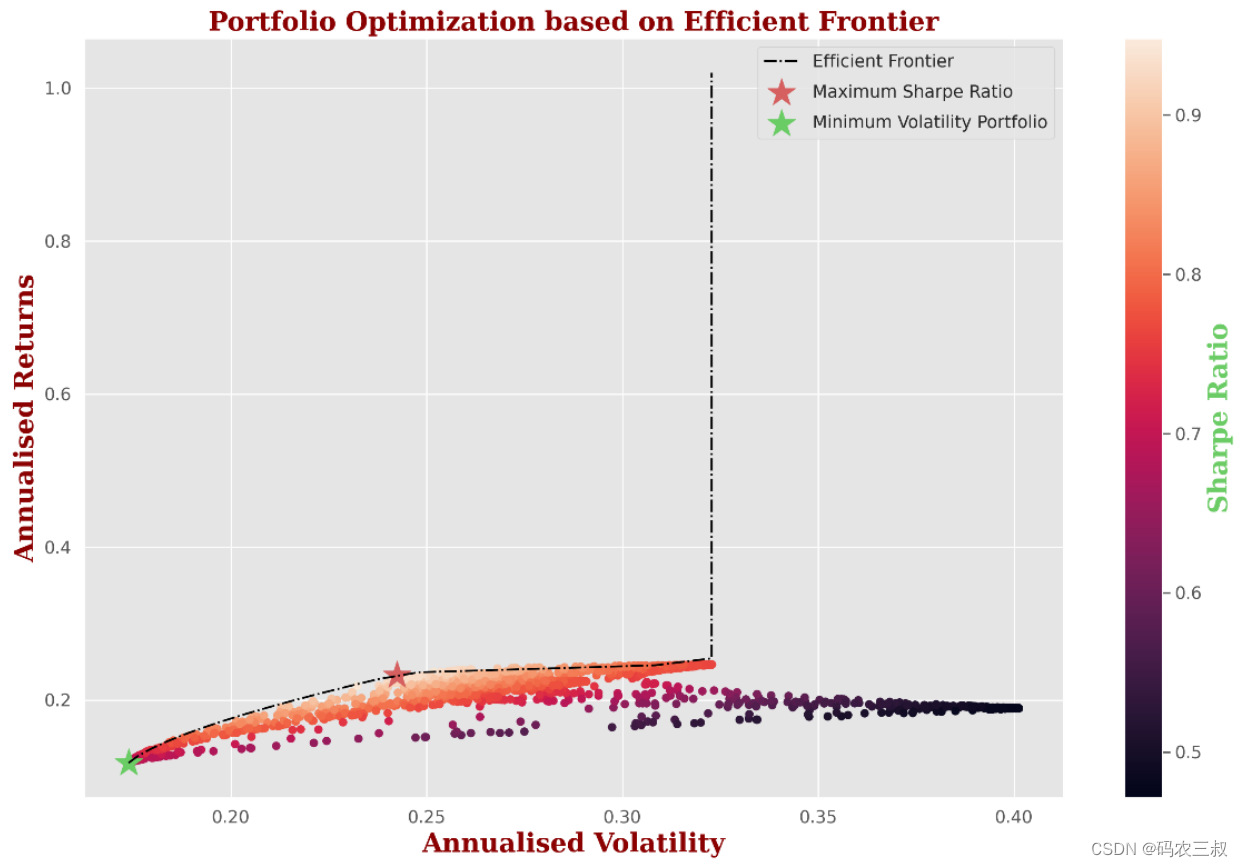
图8-8 投资组合的散点图和有效前沿
(2)现在,我们可以查看GAFAM投资组合中各资产的权重。通过如下代码查看有最高夏普比率的投资组合。当投资回报低于风险无风险利率时,夏普比率可能为负。
max_sharpe_port.to_frame().T执行后会输出:
ret stdev sharpe GOOG AAPL META AMZN MSFT GSPC
3270 0.231556 0.24312 0.849603 0.011955 0.269486 0.034679 0.209609 0.469536 0.004734(3)下面的min_vol_port.to_frame().T是一个DataFrame,其中包含最低方差投资组合的权重。
min_vol_port.to_frame().T执行后会输出:
ret stdev sharpe GOOG AAPL META AMZN MSFT GSPC
2695 0.152335 0.189673 0.67134 0.129409 0.07794 0.052775 0.016958 0.079501 0.643417查看具有最高夏普比率的投资组合权重表时,通过上面的输出结果可以看到,微软的权重比其他公司更高。相比之下,在最小方差投资组合中,Facebook的权重较低。我们可以得出结论:在这两种权重中,风险较高的那个投资组合更好。如果我们考虑风险调整后的收益,这个投资组合的夏普比率最高(0.953%),相比之下,最小方差投资组合的夏普比率较低,这意味着投资者将获得相对较高的超额收益,以换取额外的风险。
8.5.10 结论
综合而言,本项目对谷歌、苹果、Facebook、亚马逊、微软以及标准普尔500指数等公司的股市数据进行分析提供了有价值的分析。
- 波动性:对年度和月度波动性的研究显示,Meta在所有股票中表现出最高的波动性,表明其价格波动较大,存在潜在风险。这些信息有助于投资者理解这些股票的风险特征,从而做出明智的投资决策。
- 相关性:相关性分析显示标普500指数与微软、亚马逊之间以及微软与谷歌、谷歌与苹果、亚马逊与微软之间存在强烈的正相关。这些相关性表明可能存在相互依赖关系,并可以指导投资组合多元化策略。
- 风险调整回报:对夏普比率的评估提供了对股票风险调整绩效的见解。微软脱颖而出,成为夏普比率最高的股票,表明相较于其他股票和无风险投资,它具有更好的风险调整回报潜力。
总的来说,这些发现突显了在分析和选择股票进行投资时考虑波动性、相关性和风险调整回报等因素的重要性。通过充分考虑这些关键指标,投资者可以做出更为明智的决策,有效管理风险,并可能优化他们的投资组合。
本项目已经完结,欢迎点赞订阅:
(8-5-1)制作美股交易策略模型:项目介绍+准备环境-CSDN博客
(8-5-2)制作美股交易策略模型:准备环境+准备数据-CSDN博客
(8-5-3)制作美股交易策略模型:EDA+收盘价可视化-CSDN博客
(8-5-4)制作美股交易策略模型:波动性(收益率)分析-CSDN博客
(8-5-5)制作美股交易策略模型:使用有效前沿技术优化投资组合-CSDN博客
这篇关于(8-5-6)制作美股交易策略模型:投资组合模拟+可视化+结论的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



