线代专题
25考研线代攻略，老师及习题册推荐！
其实很多经验贴对大家有一定的误导 网上很多人说李永乐讲的好，确实好，但是没有说听李永乐的线代需要一定的基础 于是很多人去听完李永乐，就懵逼了，这讲的很乱啊，听的一头雾水。 其实，李永乐的基础班授课采用串联式，非常系统。他在讲解行列式时会涉及特征值，讲解向量时又会提到方程组的知识点，因此容易让人感觉有些跳跃。 你听得吃力是完全正常的。 如果你在学习线性代数时也遇到类似问题，推荐大家试试以下
避雷！线代概率论名师测评，跟对人真的可以满分
线代和概率论虽然在考研数学中占比都不大，但是也很关键 学的好的同学，线代和概率论都能满分，而学的不好的，就会丢很多没必要丢的分。 线代和概率论不像高数，线代概率论可是努努力就可以满分的，我系统的整理了一下线代和概率论价格的不错的老师的讲课特点，希望能够帮大家选到适合自己的老师： 线代老师推荐： 对于线代老师的选择，如果是基础不怎么好，我建议就去跟喻老或者汤家凤老师，如果基础还不错，
线代老师大PK，这四位胜出！
说实话，线代真的别乱跟老师 因为每个老师讲课适用的人群不一样，比如都说李永乐老师线代讲的好，但是我去听完发现，李永乐老师的线代讲的虽然好，但是对于零基础或者基础不好的考生来说，真的有点不友好，老师讲课喜欢串联后面的内容一起讲，所以很容易让人听蒙 给大家整理了四位比较火的线代老师的讲课特点，大家可以做一个参考： 如果你是零基础，真的比较推荐喻老的线代课程： 喻老的授课方式独具一格，特
线代与图形学的暧昧二三事
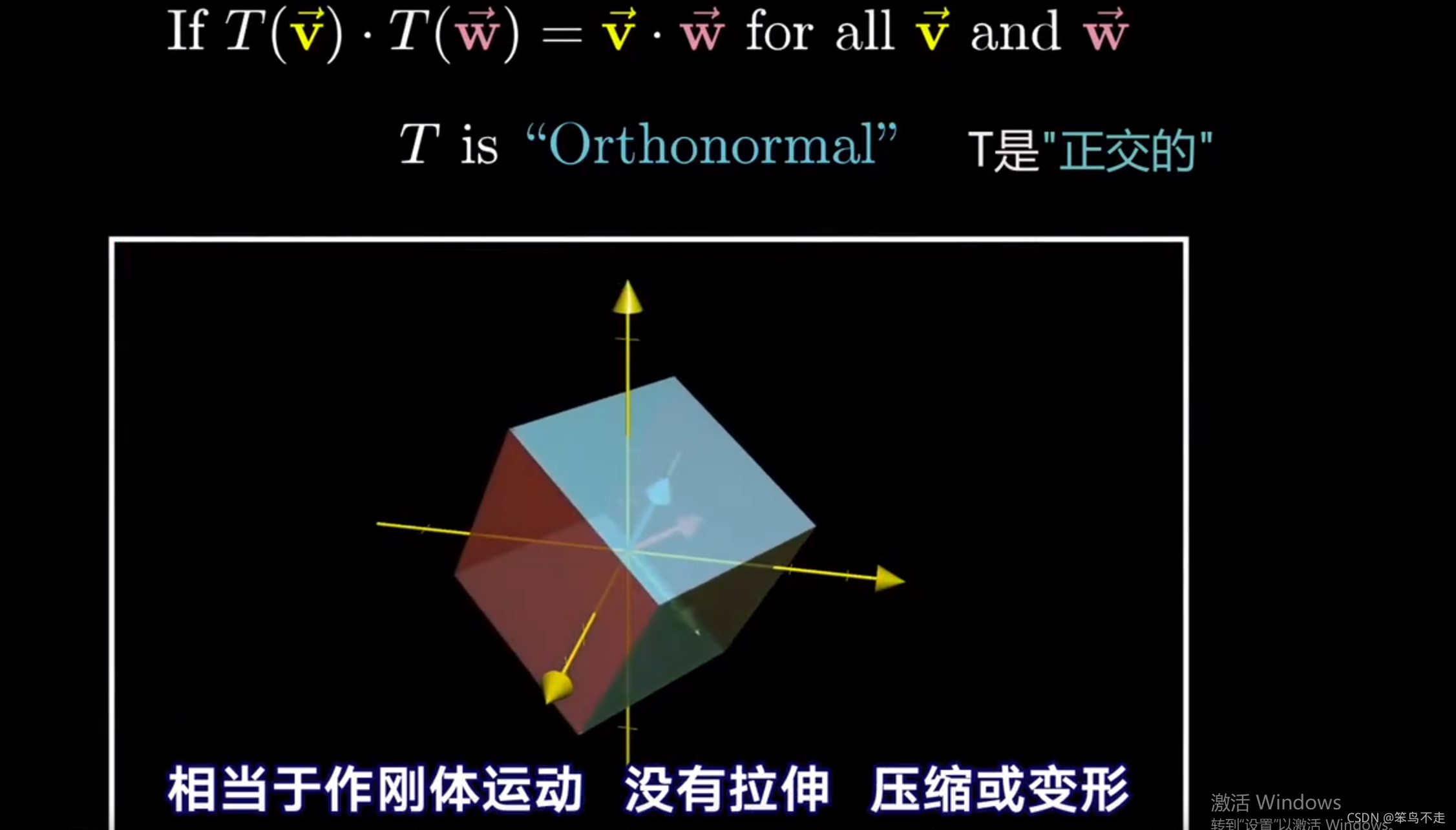
A Swift and Brutal Introduction to Linear Algebra 计算机图形学依赖于线性代数、微积分、统计...物理方面涉及到光学（波动光学：不再假设光是直线传播，作为一种光波与物体表面材质进行作用接触，如何生成不同的外观）和力学，还涉及到信号处理（分析走样、反走样技术，解决信号处理的事情），数值分析也很重要（解决一些复杂的数学计算：积分、渲染，解决递归定义的积
考研数学｜线代跟谁好，李永乐，汤家凤还是张宇？
如果线代基础不好，那建议开刚开始的时候听汤家凤老师的线代课程 汤家凤教授的线性代数课程常被忽视，多数人倾向于去听李永乐。然而，在我考研的过程中，我曾尝试听李永乐教老师的课，可能是由于我自身基础薄弱，导致我听得一头雾水。李永乐教授在授课时倾向于将后续内容串联讲解，但因为我对后续知识点尚未掌握，这种方式对于基础薄弱的学生来说，确实不太合适。 随后，我转向汤家凤老师的课程，不得不承认，汤家凤教授的授
【线代基础】张量、向量、标量、矩阵的区别
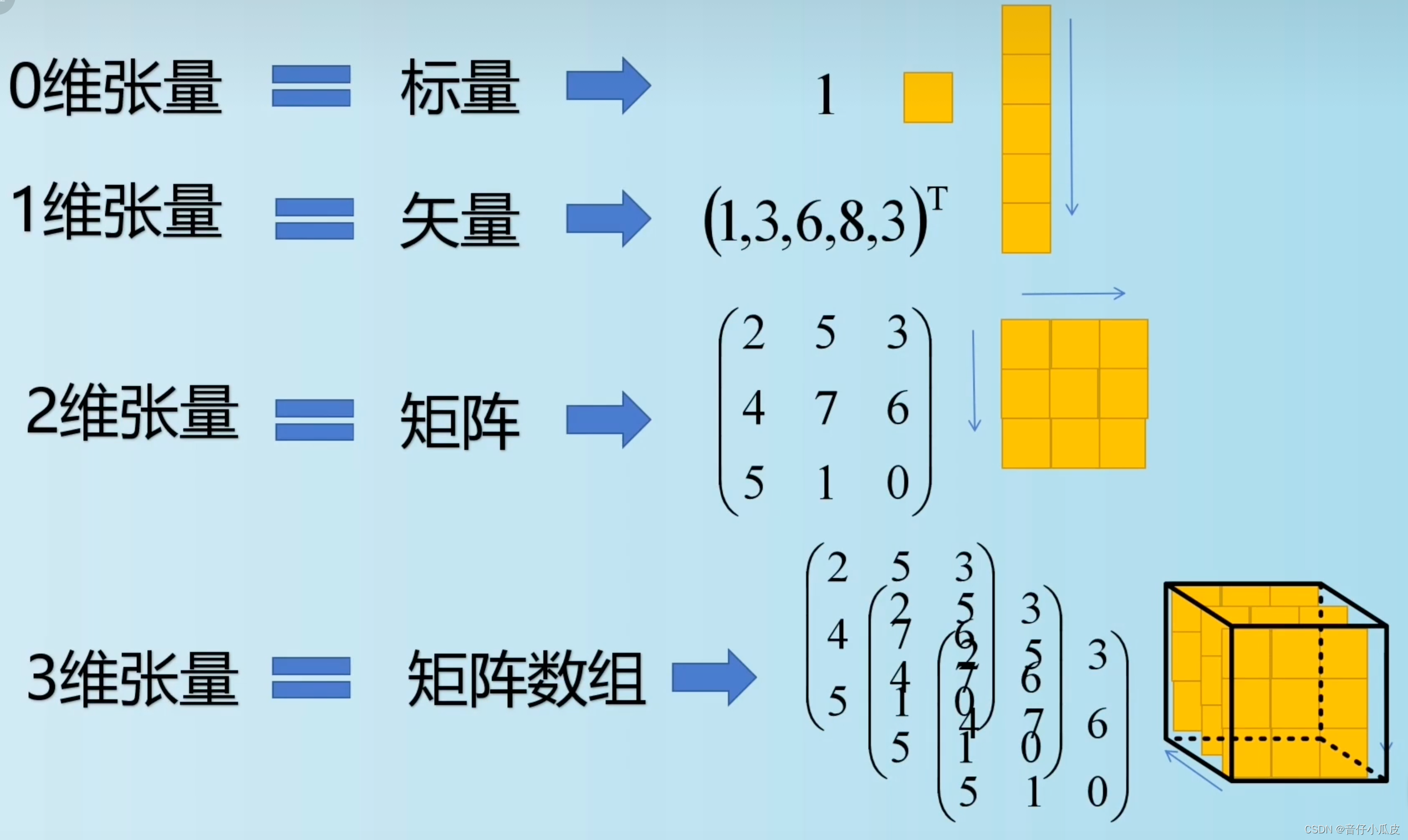
1、标量（Scalar） 纯数字，无方向性、无维度概念。因此也叫 标量张量、零维张量、0D张量 例如，x1=8，x2=1.34 x1、x2即为标量 2、张量（tensor） 具有方向性，可以理解为一个多维数组，它是标量、向量、矩阵的高维扩展，属于一个数据容器。理论上，张量是向量概念上的推广，可以理解为其在多个维度的扩展。 通常，张量的维度被称作轴(axis)，张量轴的个数也叫做阶(ra
【线代】为什么初等行变换不改变列向量/行向量的线性相关性？特征方程的简便设法？
线代中其他的一些遗留小问题，后续可能会更新。 1. 初等行变换不改变什么？（初等列变换同理） 初等行变换不改变列向量的线性相关性，也不改变行向量的线性相关性。可从以下两点来看。 ① 初等变换不改变矩阵的秩，矩阵的秩=列秩=行秩。而相关性就体现为是否满秩。 ② 不改变列向量的相关性，是因为初等行变换的过程始终保持了与原方程组同解，所以列向量间的线性关系（就是系数x1，x2……的取值，就
原神引发的一系列线代矩阵问题
由原神荒海解密引发的方程组到线代的问题 具体环境可以通过原神荒海解密完成条件，下面叙述从游戏抽出的问题模型 1.五个柱子，每个柱子都可以转动，且都有四个方向 从左至右依次编号为1，2，3，4，5 并且从上往下看（俯视角度）为顺时针旋转，切不可逆 1转动一次时3也会转动一次 2转动一次时1，3也会转动一次 3转动一次时3，5也会转动一次 4转动一次时3，5也会转动一次 5转动一次时3也会转动一次
本质矩阵8点法中的线代知识
在多视图几何的 2D 几何中，在利用八点法（Eight-point-algorithm）求解本质矩阵（Essential Matrix）的时候，出现一个将 类似二次型的形式： x T E y \mathbf{x}^{T}E\mathbf{y} xTEy 将其表示成 B E l i n e a r BE_{linear} BElinear 的过程 其中， B B B的元素 仅与 x , y
矩阵转置相关公式_「周一考研」考研数学必背公式/知识点如何整理？（高数+线代+概率）...
嗨大家晚上好，我是小R，今天是2019年9月16日，相信大多数同学已经在训练数学真题了，建议大家做真题时，每天一套，每套控制2个小时，尽量不做满3个小时，这样可以训练自己的做题专注度和速度，另外，在做题期间肯定会发现很多记不住的公式，大家可以根据自己的复习内容或者做题情况整理一份公式和知识点，方便不断翻阅和考前复习。今天就和大家以我考研期间整理公式的笔记为例，如何整理说一下考研数学必背公式/知识
2023新版PDF 高数 线代 概率论
2023新版PDF 高数 线代 概率论 考研 大学 数学 电子 教材 课本 高等数学 第8版 线性代数 第7版 概率论与数理统计 第5版 大学 数学 教材 均是2023年新出版的最新版。 部分有书签。部分可复制。 包含: 《高等数学》第8版上册 同济 《高等数学》第8版下册 同济 《高等数学习题全解指导》第8版上册 同济 《高等数学习题全解指导》第8版下册 同济 《工程数学 线性代数》第7版 同济
![线代[3]｜从增广矩阵漫谈矩阵转置对向量在四个向量子空间内的“飞舞”（第三篇）](https://img-blog.csdnimg.cn/20200427161104589.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Njk1OTY4MQ==,size_16,color_FFFFFF,t_70)
线代[3]｜从增广矩阵漫谈矩阵转置对向量在四个向量子空间内的“飞舞”（第三篇）
原创首发，转载请注明出处（CSDN：古希腊的汉密士），谢谢！ 文章目录 前言增广矩阵(Augmented matrix)｜从QR分解的角度重构增广矩阵 转置（Transpose）向量子空间（subspace）以MIT线性代数习题公开课第11题为串联脉络参考资料文章更新记录 前言 该篇文章以非齐次线性方程组为例题引出增广矩阵(A,b)的解集，配合矩阵的QR分解对增广矩阵
线代【解方程组】--猴博士爱讲课
第六课 解方程组 1/6判断方程组解的情况 判断方程组的解的情况： 齐次唯一解例题： 非齐次无解例题： 非齐次有解例题： 2/6解方程组 解方程组：共有五步 ①求增广矩阵的秩： ②变换矩阵： R=3，就变换前三行，前三列，为单位矩阵的形式 ③ 根据②得到的矩阵变回方程组： ④设未知数： ⑤整理成标准型，再用刚刚设的未知数替代
线代本质/矩阵左乘右乘的数学意义
对矩阵A而言， BxA（左乘）是对A进行行变换 AxB（右乘）是对A 进行列变换 如图 这里再讲一下A*v的几何意义; A = [ 1 − 1 1 2 ] A=\begin{bmatrix} 1 & -1 \\ 1 &2 \end{bmatrix} A=[11−12], v = [ 1 1 ] v=\begin{bmatrix} 1 \\ 1 \end{bmatrix} v=[11
