本文主要是介绍线代本质/矩阵左乘右乘的数学意义,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对矩阵A而言,
BxA(左乘)是对A进行行变换
AxB(右乘)是对A 进行列变换
如图
这里再讲一下A*v的几何意义;
A = [ 1 − 1 1 2 ] A=\begin{bmatrix} 1 & -1 \\ 1 &2 \end{bmatrix} A=[11−12], v = [ 1 1 ] v=\begin{bmatrix} 1 \\ 1 \end{bmatrix} v=[11]
A v = [ 0 3 ] Av=\begin{bmatrix} 0 \\ 3 \end{bmatrix} Av=[03]
这个在几何上怎么理解呢?
在上面部分我们知道,这个操作就是对A的列进行操作,取1份[1;1],一份[-1;2],相加得到[0,3]
那实际上也就是以A的列向量[1;1] [-1;2]分别为x\y轴构建新的坐标系,新坐标系下的[1,1],在原来的[1,0] [0,1]坐标系下表现为[0,3]
也就是Ev=v,是以E([1,0] [0,1])轴为基,v为坐标;
而因为Av=EAv,所以该表达是先以A([1,1] [-1,1])轴为基,v为该坐标系下的坐标;再放到E坐标系下,发现是[0,3]
或者更直接的这么理解:变换后x跑到[1;1] ,y跑到 [-1;2]了,由于线性变换是等距平行四边形模样,且原点不动,所以借助变换后的xy定位变换后的vector的位置:x[1;-1]+y[-1;1]
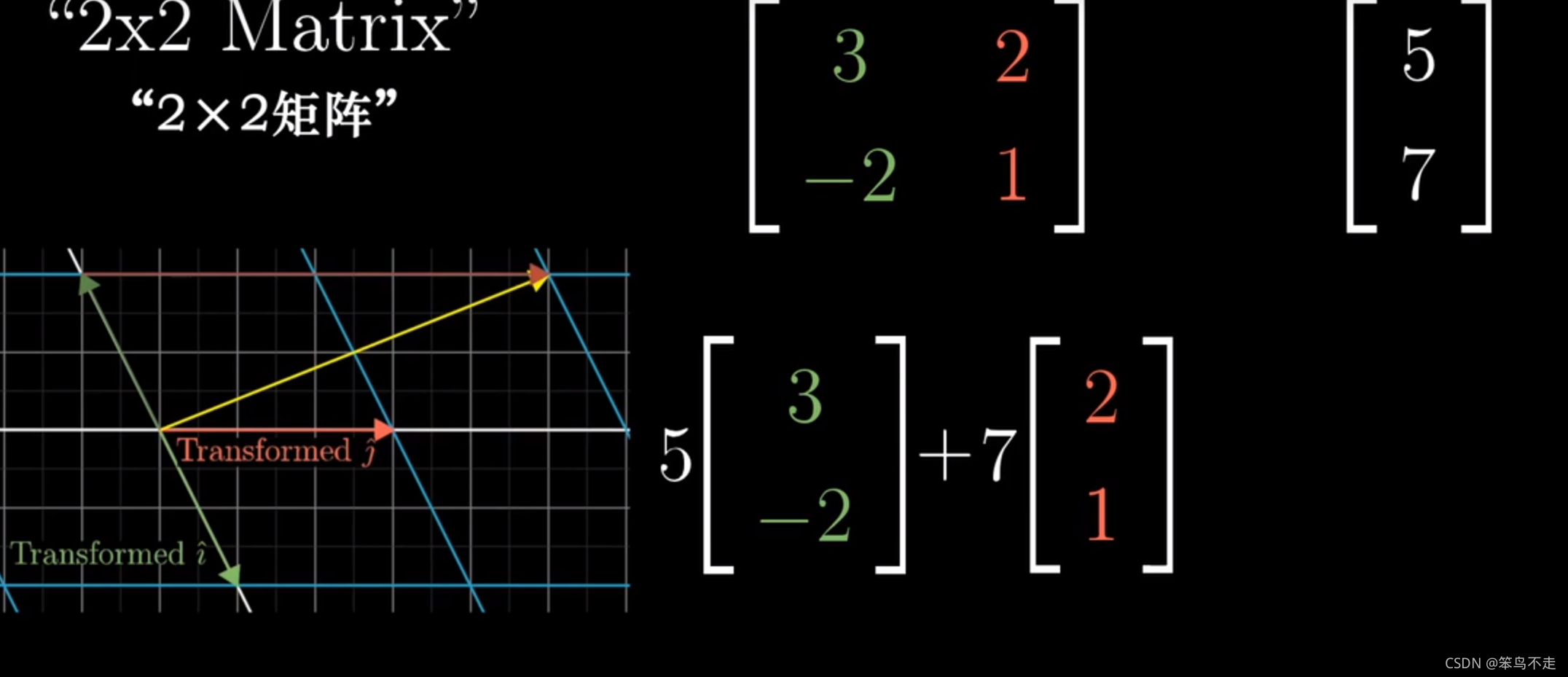
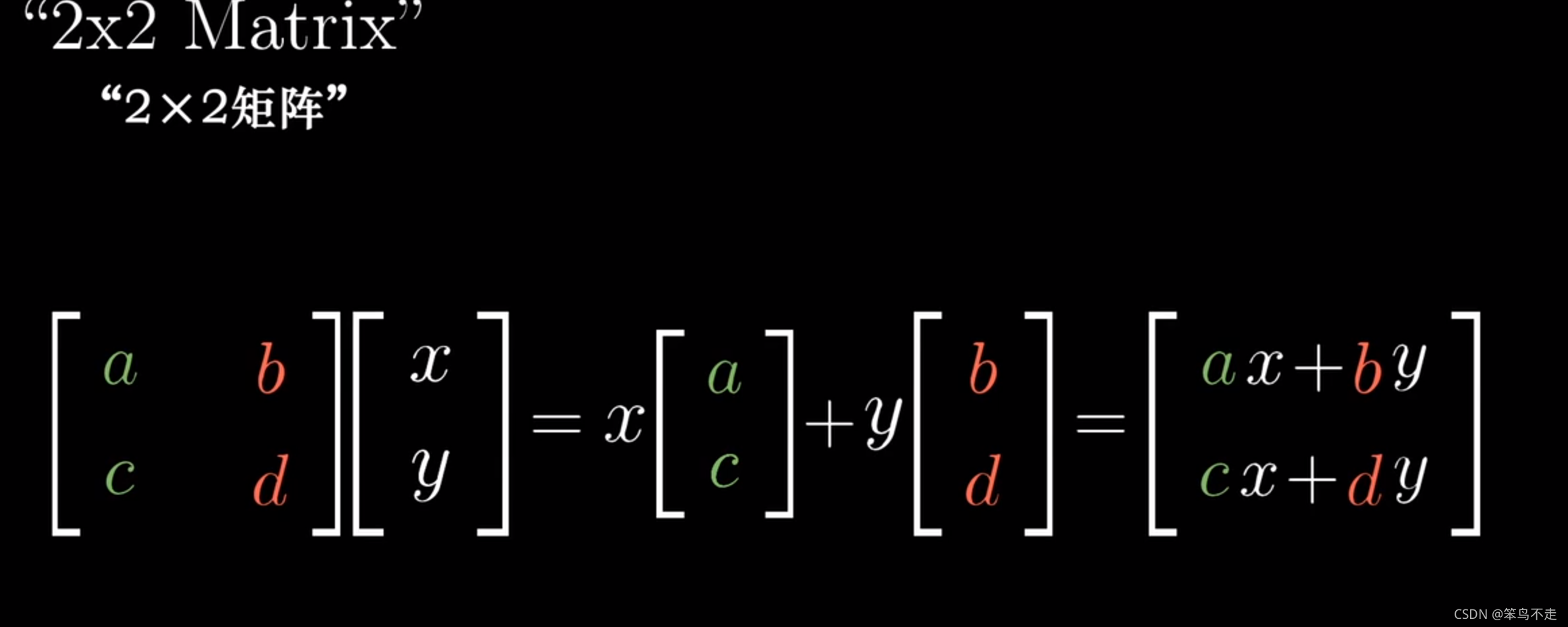
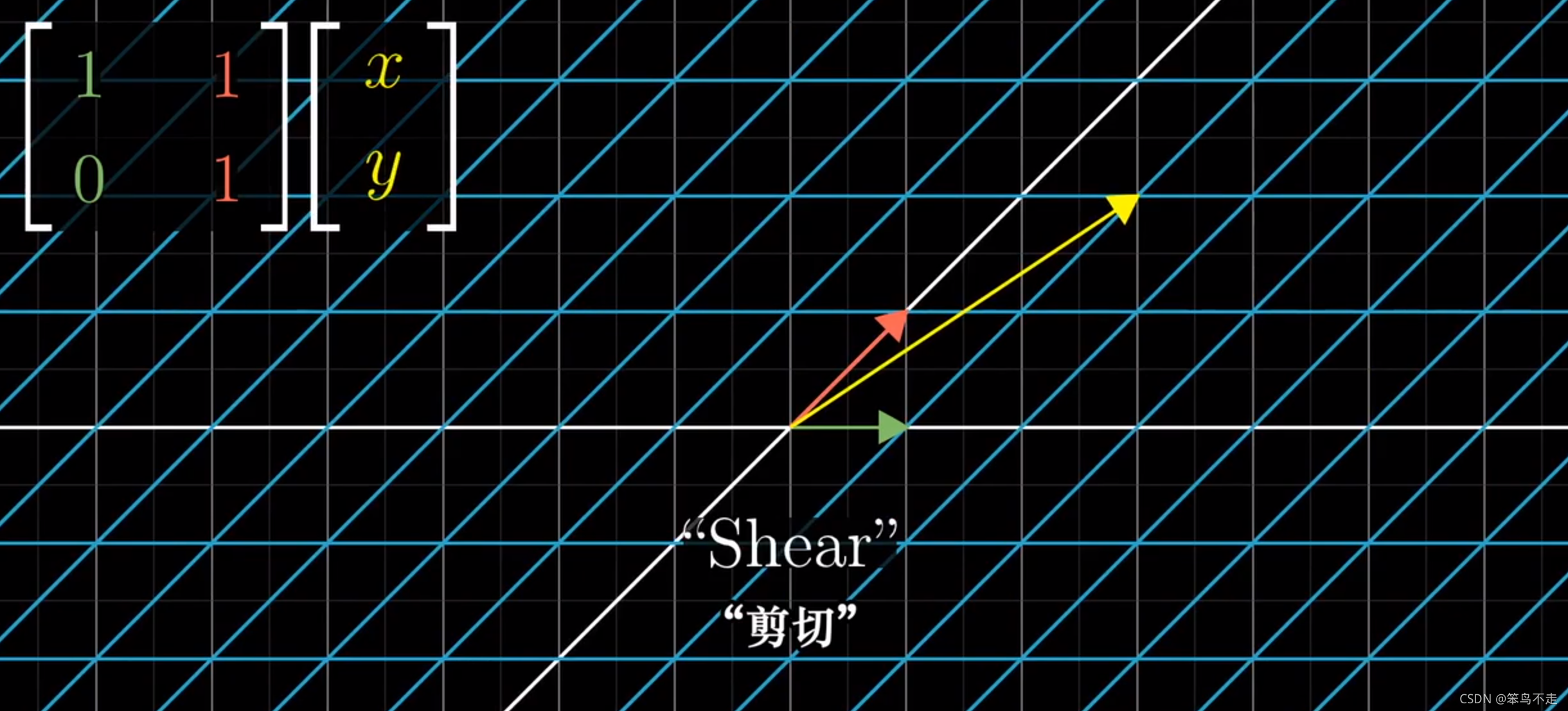
注意到这里原点不变,不然就不是线性变换,而是仿射变换。变换是线性的定义是满足(1)Add: L(vector1+vector2)=L(vector1)+L(vector2) (2)Scale: L(c vector)=c L(vector) 所以原点是固定的
白色部分是E坐标(锚),绿色、红色部分是新坐标系;取x绿, y红,相加,新坐标系中的[x,y]表现为E坐标系中的x绿+y红色。
所以A的两个列就是一个很好的记录,比如我们要旋转一个向量(x,y),假设E坐标系中的(0,1) (1,0)旋转后是A的第一二列,那么Ax就是旋转后的向量了
而det(A),就是旋转/伸缩(线性变换)后 绿,红线围成的平行四边形的面积。
假设A不满秩,也就是两条新坐标轴将共线,面积为0,det(A)=0。
当det(A)<0,说明是坐标轴翻转了(oriented?),即翻了个面,本来y轴在x轴左边的,现在跑到右边去了。
对于三维空间,det(A)是体积,表示变换后的x,y,z轴围成的cube的体积。那么原本在三维空间中的某个物体,变换后体积也相应变大为det(A)倍数。当A不满秩序,也就是有两/三条变换后的轴共线了,cube压成了平面/直线,平面/直线的体积==0, det(A)=0。当det(A)<0,就是翻转了,右手法则(右手拇指Z,食指x,中指y)变成了左手法则(右手拇指Z,食指x,中指y),本来y轴在x轴左边的,现在跑到右边去了。
det(AB)=det(A)det(B):因为AB是复合变换;先变换B,单位cube面积变化为det(B)倍;然后变换A,在上一部的基础上再变化为det(A)倍,也就是最终det(A)*det(B)倍。==》 det(A)det(B) == det(A) * det(B)
A的特征向量,对应则在这个旋转伸缩过程中不会旋转只伸缩的向量(旋转轴),对应的特征值,是指这个旋转轴方向上的伸缩量,只伸缩,不旋转。 A v = λ v Av=\lambda v Av=λv
所以为什么一个N重特征值 λ 1 \lambda_1 λ1对应着N个不同的特征向量(旋转轴)呢?这里其实是因果倒置了,逻辑是:我有N个旋转轴,不会跟着变换旋转,而只是伸缩;它们的伸缩量刚好都是是 λ 1 \lambda_1 λ1;
是这样的:方阵特征值对应的基础解系包含的向量个数不大于特征根的重数。比如说一个二重特征根它对应的特征向量基础解系的个数可能为2也可能为1。有的课本把特征根的重数叫做特征值的代数重数,把特征值对应特征向量的基础解系个数叫做特征值的几何重数,于是刚才所描述的原理也可以这么叙述:方阵特征根的几何重数不大于代数重数。那么题主可能要问,特征根几何重数等于代数重数的方阵,和特征根几何重数小于代数重数的方阵有什么区别呢?区别在于,如果一个方阵的所有特征根的几何重数均等于其代数重数,那么这个方阵是可以相似对角化的,如果这个方阵中只要有一个(或以上)的特征值的几何重数小于其代数重数,那么这个方阵就是无法相似对角化的。
再一个,我们知道实对称矩阵的特征向量都是正交的;那么普通矩阵,一个 λ 1 \lambda_1 λ1对应的多个特征向量,我们通常都将它们单位正交化;那为什么单位正交化后,还是这个特征向量/值呢? 因为从公式上来讲,特征向量的线性组合还是特征向量 A ( v 1 + v 2 ) = A v 1 + A v 2 = λ 1 v 1 + λ 1 v 2 = λ 1 ( v 1 + v 2 ) A(v_1+v2)=Av_1+Av_2=\lambda_1v_1+\lambda_1 v_2=\lambda_1(v_1+v_2) A(v1+v2)=Av1+Av2=λ1v1+λ1v2=λ1(v1+v2),即 v 1 + v 2 v_1+v_2 v1+v2仍然是特征向量,特征值即伸缩因子仍然是 λ 1 \lambda_1 λ1。但是几何上怎么理解???:
λx=Ax表示特征向量相当于沿此方向进行特征值倍数的放缩,如果一个特征值有两个线性无关的特征向量,说明在两个方向上均匀缩放,那么用这两个线性无关特征向量作为基表示整个平面,平面上处处都是均匀缩放
当A为旋转变换时,没有任何一条线是原地不动只伸缩的
因此,特征值没有实数解
也就是说,求出来特征值是虚数or复数的,对应着某种旋转
投影和特征向量
另外,对称矩阵必可以对角化(特征分解),有什么好处呢?
我们知道 (源自泛函分析绪论r)

也就是上面讲的,
“A的特征向量,对应则在这个旋转伸缩过程中不会旋转的向量(旋转轴),对应的特征值,是指这个旋转轴方向上的伸缩量,只伸缩,不旋转。”
因此


解方程Ax=y,x是待求解向量;就是求在变换A下,哪个x会变成变换后的y。
当A不满秩,也就是有的变换后的轴共线了,整个平面被变换为一条先/面,总之被压缩了,做不到一一映射了,也就找不到唯一的那个x; 逆变换也就不存在,也就是A不可逆。当然,当x本身就在压缩后的线上,那就能找到。
A − 1 A x = x A^{-1}Ax=x A−1Ax=x,因为 A − 1 A = E A^{-1}A=E A−1A=E, E x = x Ex=x Ex=x,也就是两条轴没变换,自然x或空间内的其他向量也没变换。
det(A)!=0,没坍缩,满秩。
秩:变换后的空间的维数,那就是看A的列向量张成的空间的维数
Null Space 零空间/Kernel 核:变换后落在原点的向量的集合!(二维里有一条线上的点(向量)落在原点,三维里有一个面落在原点)
Ax=0即可求解
非方阵
(1)低维到高维
A = [ 1 4 2 5 3 6 ] A=\begin{bmatrix} 1 & 4\\ 2&5\\ 3&6 \end{bmatrix} A=⎣⎡123456⎦⎤,
输入空间为2维
v = [ 1 1 ] v=\begin{bmatrix} 1 \\ 1 \end{bmatrix} v=[11]
A v = [ 5 7 9 ] Av=\begin{bmatrix} 5\\7\\9 \end{bmatrix} Av=⎣⎡579⎦⎤,
可以看到,A把2维的v变换到3维空间中了。
原本2维空间中的x轴 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01],被变换到了三维空间中的 x ^ = [ 1 2 3 ] \hat{x}=\begin{bmatrix} 1 \\ 2\\ 3\\ \end{bmatrix} x^=⎣⎡123⎦⎤;
原本2维空间中的y轴 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10],被变换到了三维空间中的 x ^ = [ 4 5 6 ] \hat{x}=\begin{bmatrix} 4 \\ 5\\ 6\\ \end{bmatrix} x^=⎣⎡456⎦⎤
对应的原本2维空间中的v,被变换到了三维空间中的 A v = [ 5 7 9 ] Av=\begin{bmatrix} 5\\7\\9 \end{bmatrix} Av=⎣⎡579⎦⎤
A:3*2,将2维变换到3维空间
(但是原本2维空间被限制在3维空间的一个面中!有变换后的 x ^ y ^ \hat{x}\hat{y} x^y^张成的一个三维空间中的一个面)

这里A仍然是二维意义上的满秩的
(2)高维到低维
如A:23
A = [ 3 1 4 1 5 9 ] A=\begin{bmatrix} 3 &1&4\\ 1&5&9 \end{bmatrix} A=[311549],
三维空间中的 [ 1 0 0 ] \begin{bmatrix} 1\\0\\0 \end{bmatrix} ⎣⎡100⎦⎤变换到了二维中的 [ 3 1 ] \begin{bmatrix} 3\\1 \end{bmatrix} [31],
[ 0 1 0 ] \begin{bmatrix} 0\\1\\0 \end{bmatrix} ⎣⎡010⎦⎤变换到了二维中的 [ 1 5 ] \begin{bmatrix} 1\\5 \end{bmatrix} [15],
[ 0 0 1 ] \begin{bmatrix} 0\\0\\1 \end{bmatrix} ⎣⎡001⎦⎤变换到了二维中的 [ 4 9 ] \begin{bmatrix} 4\\9 \end{bmatrix} [49]
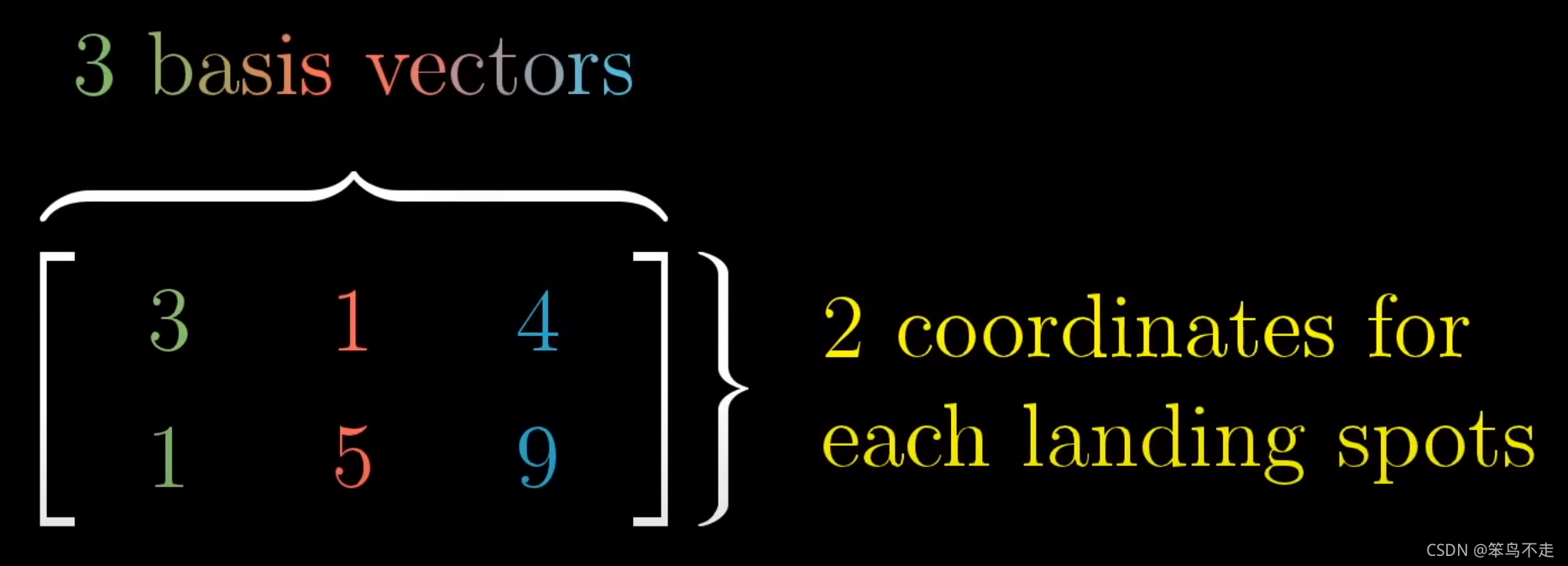
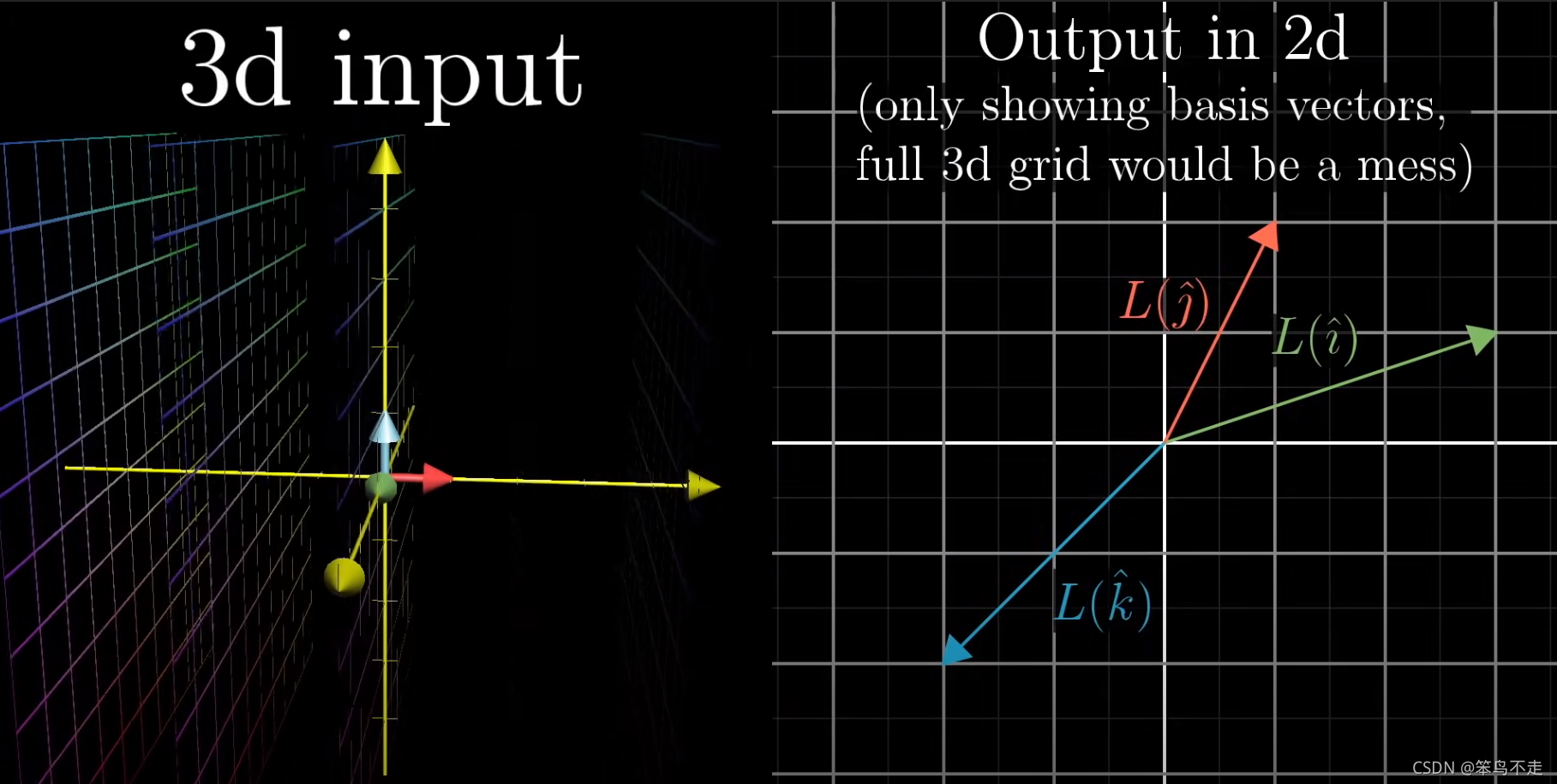
(3) A: 21 二维变换到1维
如A:2*3
A = [ 1 2 ] A=\begin{bmatrix} 1&2 \end{bmatrix} A=[12],
2维空间中的 [ 1 0 ] \begin{bmatrix} 1\\0 \end{bmatrix} [10]变换到了1维中的 [ 1 ] \begin{bmatrix} 1 \end{bmatrix} [1],
[ 0 1 ] \begin{bmatrix} 0\\1 \end{bmatrix} [01]变换到了1维中的 [ 2 ] \begin{bmatrix} 2 \end{bmatrix} [2],
这个变换与点积(dot product)紧密相关

扩展空间的概念,函数在作为空间中的向量/元素——函数空间
满足下列定理的空间,就可以利用线性代数所学的这套理论来套
线性变换——算子(函数空间到函数空间,比如对x变上限积分、对 x 2 x^2 x2求导后仍然是函数)
特征向量——特征函数

多项式空间比较容易类比向量空间( 1 , x , x 2 , ⋯ , x n , ⋯ 1,x,x^2, \cdots,x^n,\cdots 1,x,x2,⋯,xn,⋯为基/轴,无穷个 )
傅里叶变换也是, e j k w t e^{jkwt} ejkwt为基(轴), s ( t ) s(t) s(t)在各轴上的坐标就是 s ( t ) s(t) s(t)在各个轴上的投影——内积(因为 e j k w t e^{jkwt} ejkwt模长1不用除掉)——也就是 ∫ s ( t ) e j k w t d t \int s(t)e^{jkwt}dt ∫s(t)ejkwtdt
(线代的内积是离散内积,相乘再相加;到了连续变量上,相加就是积分了)
所以所谓“检波”,其实也就是在求内积,也就是求投影( ∣ a ∣ ∣ b ∣ c o s θ = ∣ a ∣ c o s θ |a||b|cos\theta=|a|cos\theta ∣a∣∣b∣cosθ=∣a∣cosθ)
正交变换后,

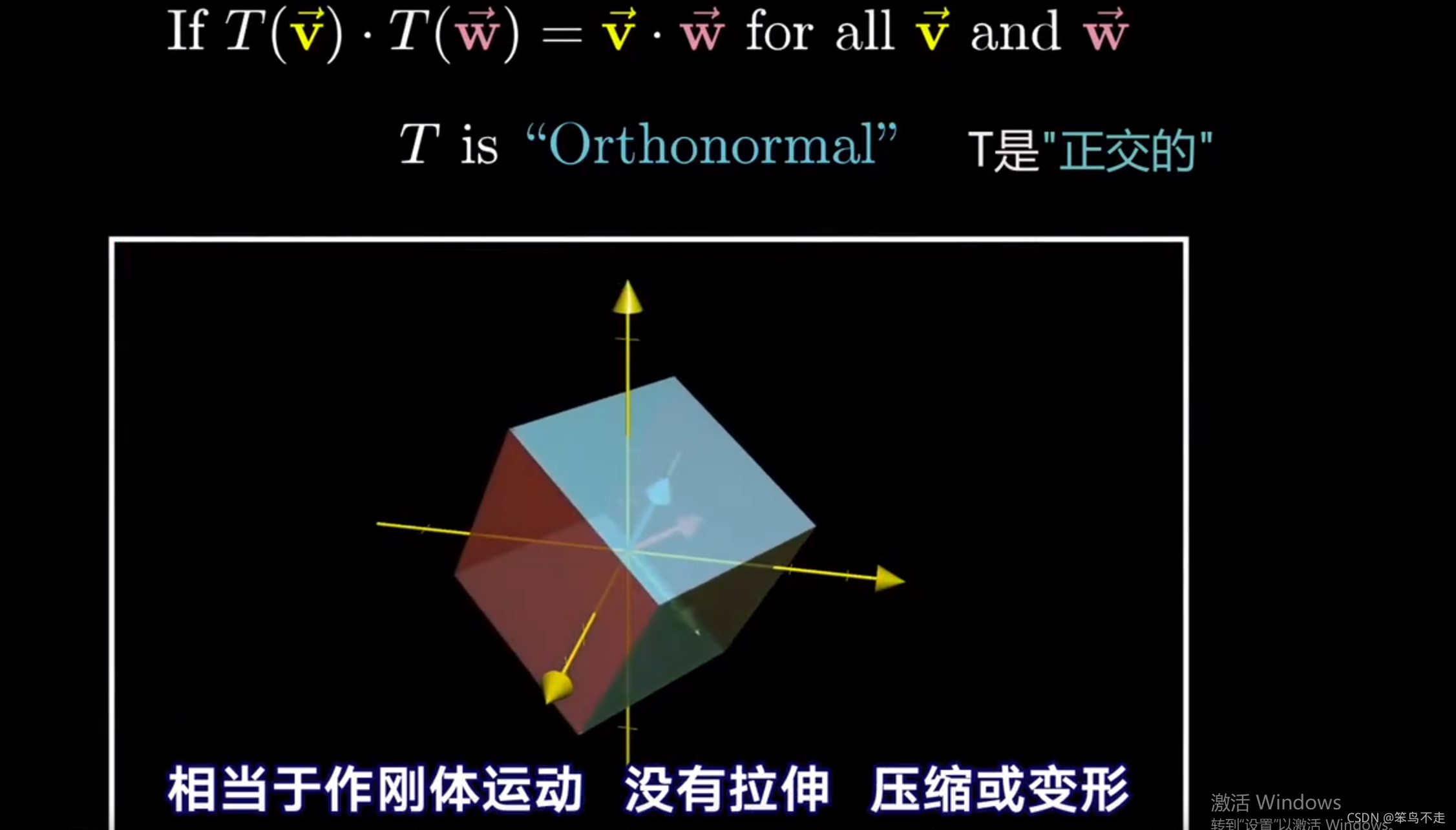
这篇关于线代本质/矩阵左乘右乘的数学意义的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






