本文主要是介绍线代知识点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、行列式
n阶行列式:
这里 表示对所有n级排列求和,
表示排列
的逆序数。每项由不同行、不同列的n个元素乘积组成,没项的正负号取决于 逆序数
。
行列式性质:
1、行列互换,其值不变
2、行列式中某行/列元素全为0,则行列式为0
3、行列式中某行/列元素有公因子k(k不为0),则k可提到行或列外面
4、行列式某行/列元素均是两个元素之和,则可拆成两个行列式之和
5、行列式两行/列互换,值取反
6、行列式两行/列元素相等或对应成比例,行列式为0
7、行列式中某行/列的k倍加到另一行/列,行列式值不变
余子式&代数余子式:
在n阶行列式中,去掉元素 所在的第i行,第j列元素,有剩下的元素按原来的位置于顺序组成的n-1阶行列式称为元素aij的余子式,记成
,
余子式 乘
后称为
的代数余子式,记
克拉默法则:
n个方程n个未知量构成的非齐次线性方程组
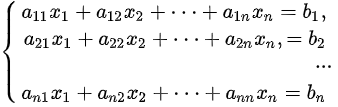
的系数行列式,则方程组有唯一解,且
,i=1,2,3.....其中
是
中第i个元素替换成方程组右端的常数项
后所构成的行列式。
推论:
若包含n个方程n个未知量的齐次线性方程组(即 都为0)的系数
,则方程组有唯一0解,反之,若齐次线性方程组有非零解,则其行列式等于0
矩阵:
特殊矩阵:零矩阵(所有元素都为零)、单位矩阵(主对角线元素均为1,其余元素为0)、数量矩阵(数k和单位矩阵的乘积)、对角矩阵(非主对角元素均为0)、上(下)三角矩阵(当i>/<j时,,为上/下三角矩阵)、对称矩阵(
)、反对称矩阵(
)、正交矩阵(
)
矩阵的逆:n阶方阵,AB=BA=E,B是A的逆矩阵
向量:
线性判别五大定理:
1、向量 可由向量组
线性表出
非齐次线性方程组
有解
2、向量组线性相关
齐次线性方程组
有非零解
3、向量组线性相关的充要条件为:向量组中至少一个向量可由其余n-1个向量线性表出
4、若向量组线性无关,而向量组向量组
线性相关,则 b 可由
线性表出,且表出法唯一
5、若向量组 中的每一个向量
都可由向量组向量组
线性表出,且s>t,则向量组
线性相关,若(1)中的每一个向量
均可由(2)线性表出,且(1)线性无关,则
向量空间
定义1、
若 是
中线性无关的有序向量组,则任一向量
均可由
线性表出,
则称有序向量组
是
的一个基,基向量的个数n成为向量的维数,而
称为向量
在基
下的坐标,或 称为
的坐标行(列)向量
定理2、
若 和
是
的两个基,且有关系
则称上式为由基
到基
的基变换公式,矩阵C称为由基
到基
的过渡矩阵,C是可逆矩阵
定理3、
设 在基
和
下的坐标分别为
,即
又基
到基
的过度矩阵为C,即
,则
得
或
,称为坐标变换公式
正交变换:
设A是n阶方阵,满足 ,则称A是正交矩阵
设A是正交矩阵,则称 为正交变换,正交变换保持向量内积不变,即保持向量长度,两向量间的夹角不变
线性方程组
1、齐次线性方程组:
当r(A)=n时( 线性无关),Ax=0有唯一零解
当r(A)<n时,Ax=0有非零解,且有n-r个线性无关解
2、非齐次线性方程组:、
若 (b不能由
线性表出),Ax=b无解
若 (
线性无关,且能线性表出b),Ax=b有唯一解
若 (
线性相关,且能线性表出b),Ax=b有无穷解
特征值
设A是n阶方阵, 是一个数,若存在n维非零向量\xi ,使得
则称
是A的特征值,
是A对应于特征值
的特征向量。
,因为
,所以
,称为A的特征方程
二次型
n 元变量 的二次齐次多项式
称为n元二次型,简称二次型。称 为二次型
的矩阵表达式,A是对称矩阵
线性变换:
对于n元二次型 ,若令
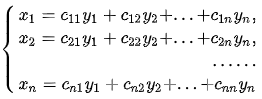
记 为
系数矩阵,
,则可写为:
上式称为从
到
的线性变换,若
可逆,即
,则称为可逆线性变换。现给出
,令
,则
记
,则
此时,二次型
通过线性变换
得到一个新二次型
可逆线性变换不会改变二次型的秩。
矩阵合同:
设A、B为n阶实对称矩阵,若存在可逆矩阵C,使得 则称A与B合同,记
,此时称
为合同二次型
可以看出,在二次型背景下,A表征的是 的“形态”,B表征的是
的“形态”。在二次型中,A与B合同,就是指在同一个二次型在可逆线性变换下的两个不同状态的联系。
二次型的标准型、规范型
若二次型中只有平方项,没有交叉项(即所有交叉项的系数全为零)的二次型称为标准型,若标准型中,系数仅为1,0,-1的二次型称为规范型。
任何二次型均可通过配方法(可逆线性变换)化成标准型及规范型:任何对称矩阵 A ,必然存在可逆矩阵 C ,使得
也可以通过正交变换化成标准型:任何实对称矩阵 A ,一定存在正交矩阵 Q ,使得
惯性定理:
无论选取什么可逆线性变换,将二次型化成标准型或规范型,其正项之数p,负项之数q都是不变的,p称为正惯性指数,q称为负惯性指数。
正定二次型:
n元二次型 ,若对任意的
,均有
,则称f为正定二次型,称二次型对应矩阵A为正定矩阵
二次型正定的必要条件:
这篇关于线代知识点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









