矩阵转置相关公式_「周一考研」考研数学必背公式/知识点如何整理？（高数+线代+概率）...

嗨大家晚上好，我是小R，今天是2019年9月16日，相信大多数同学已经在训练数学真题了，建议大家做真题时，每天一套，每套控制2个小时，尽量不做满3个小时，这样可以训练自己的做题专注度和速度，另外，在做题期间肯定会发现很多记不住的公式，大家可以根据自己的复习内容或者做题情况整理一份公式和知识点，方便不断翻阅和考前复习。今天就和大家以我考研期间整理公式的笔记为例，如何整理说一下考研数学必背公式/知识点。（工作组花了几天时间整理成pdf共18页）

考研数学一个很重要的点就是要记住大量的计算公式和知识点，对我来说，记公式主要有3个方法：

1. 通过做题去加深记忆。每做一道题，你对公式的理解和记忆一定会进步很大，这是毋庸置疑的。
2. 整理公式和知识点。通过自己的整理，一来可以把不懂的共识理解一下，二来可以归类记忆，我下面的线性代数公式，就是一个很典型的例子。
3. 默写总是记不住的公式。有些公式可能没办法通过多做题记住（比如中心极限定理的各个公式，考得不多)，就真的要在草稿纸多默写啦，我记得自己当时把一个公式每天早上一过来就默写一遍，默写了一个月，记得很牢很牢。

下面用我考研时整理的部分笔记举例讲述一下整理的特点，请认真看哦！

ps：以下图片均整理自小R的笔记，需要pdf 的同学可以拉到文末免费获取。

高数01

高数最开始要背的就是积分表，把自己一直背不上的积分记在笔记上，做题发现自己总是忘记的时候不要崩溃……默默翻阅一下笔记，争取下次可以记住：

其次就是自己一直记不住的泰勒公式：比较难，也考得没有以前那么勤快，但是掌握了还是很有成就感的。

还有幂级数的展开，这个真的很重要很重要，太经常用到了！

线代02

线代最重要的就是矩阵和行列式公式表，我当时手动整理下面的表格花了很长时间，真的超值超值超值！因为这个表涵盖了所有要背的相关式子，而且整理的时候是会分类整理的，把转置和转置的放在一列，逆矩阵和伴随矩阵相关的公式放在另外两列，真的很好记！而且应该是独一无二的，因为当时自己也买了一些公式大全，都没有自己整理的全。

忘记的时候只需要看一下这个表顺便默写一下就可以。（我当时抄写在便利贴然后贴在桌子上，真的是随看随记。）

这个表如果你们自己没有的话，可以把我的打印下来贴在显眼的位置看。

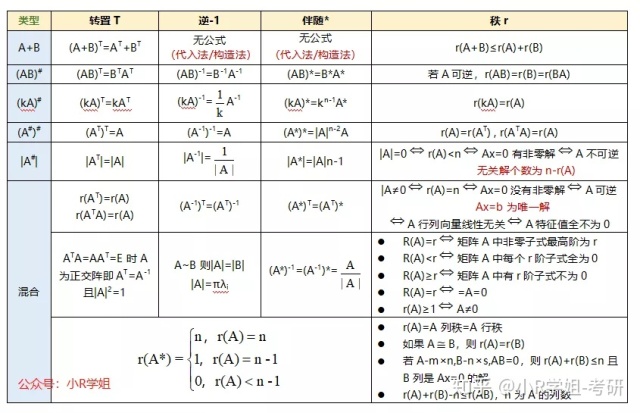
还有向量表：

概率03

概率中我认为最重要的就是几个常考的分布表格，我将这些分布都整理在一页纸，记下每个的期望和方差，方便记忆：（部分）

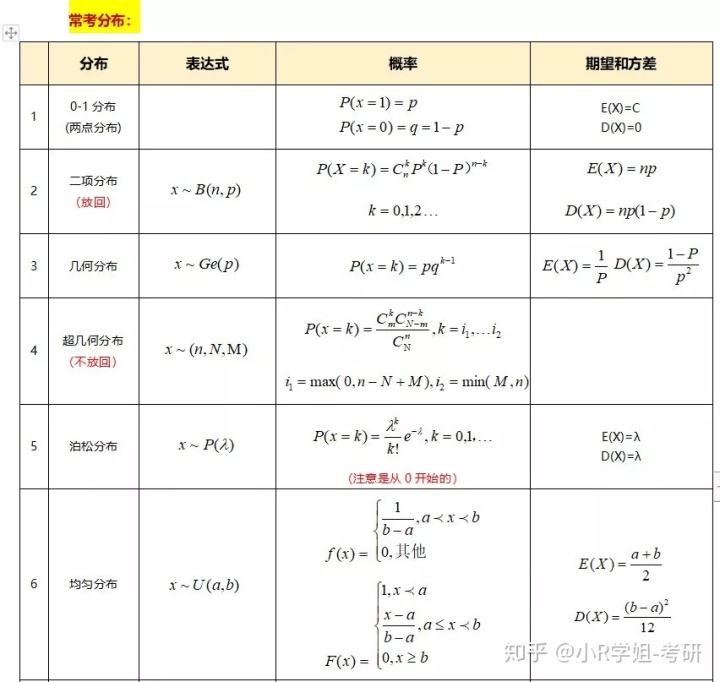
通过我上面的部分笔记，大家能看出来特点吗？？？

简单来说要做到4点：

1.只记自己记不住的知识点和公式！没必要重复浪费时间在已经记住的公式上，所以这个整理过程真的很适合二轮以后做，因为你知道自己哪里一直记不住，哪里真的掌握不好。

2.归类整理。比如线代矩阵表格那里，一定要归类！归类！归类！归类能够让人联想记忆，效果会更好！

3.重要的知识点。说实话，能在大纲里的都是重要的，但是也难免有一些真的很赘述也十年不考的点，这些可以不记或者说记不上也没关系，考场前可以迅速过一下，应付万一。

4.版面好看。不管是手写还是电脑打印，版面一定要好看好看好看，不然看不下去……

好啦，数学是考研过程中一道比较难的坎，每天复习，认真分析，相信你一定可以获得理想的分数！

小R数学笔记只有数学三的知识点，数学一少数缺少的知识点需要大家自己去补充。

获取笔记的方式：转发这条推送到超过100人的考研群或者朋友圈空间（所有人可见，10min以上），将截图发送至公众号后台，审核没问题就会发哦（24h内）！

希望理解哦，公式我们整理了好久。

考研加油！

编 辑丨小 R

策 划丨小 R

审 核丨小R学姐工作组

提 醒丨关注“小R学姐”，了解考研精彩干货

我们专注考研干货

我们只发原创文章

我们了解你，因为我们曾经是“你”