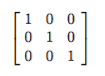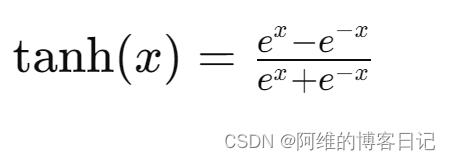转置专题
![[深度学习]转置卷积(Transposed Convolution)](https://img-blog.csdn.net/20171016205530158?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMzI1MDQxNg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
[深度学习]转置卷积(Transposed Convolution)
一.写在前面 在GAN（Generative Adversarial Nets， 直译为生成式对抗网络）中，生成器G利用随机噪声Z，生成数据。那么，在DCGAN中，这部分是如何实现呢？这里就利用到了Transposed Convolution（直译为转置卷积），也称为Fractional Strided Convolution。那么，接下来，从初学者的角度，用最简单的方式介绍什么是转置卷积，以及
数学基础 -- 线性代数之共轭转置矩阵
共轭转置矩阵 1. 共轭转置矩阵的定义 共轭转置矩阵（Hermitian transpose）是线性代数中的一个重要概念，特别是在处理复数矩阵时经常使用。它的定义包括两个步骤： 转置：将矩阵的行和列互换。共轭：对矩阵中的每个元素取复共轭，即将复数的虚部取负。 数学表达 对于一个 m × n m \times n m×n 的复矩阵 A A A ，其共轭转置矩阵 A † A^{\dag
如何实现一个二维数组的转置
#include<iostream>#include<stdlib.h>#include<time.h>using namespace std;void printMatrix(int* ,int ,int );void tranMatrix(int* ,int ,int );int main(){int A[5][5]={};srand((unsigned)time(NULL));/
1164C语言实验——矩阵转置
题目描述 输入N*N的矩阵，输出它的转置矩阵。 输入 第一行为整数N（1≤N≤100）。 接着是一个N*N的矩阵。 输出 转置矩阵。 示例输入 21 21 2 示例输出 1 12 2 #include <stdio.h>int main(){int i,j,n,d[100][100];scanf("%d",&n);for (i=0;i<n;i++)
【Pytorch】tensor 转置 t()
tensor的t()属性实现转置 >>> import torch>>> x = torch.Tensor([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])>>> x1 2 3 4 56 7 8 9 10[torch.FloatTensor of size 2x5] >>> x.t()1 62 73 84 95 10
JAVA之矩阵的转置
package test;import java.util.Scanner;public class DEMO2 {public static void main(String[] args) {int m,n,min,i,j,k;Scanner s=new Scanner(System.in); System.out.println("请输入您想创建的矩阵的行数与列数,m为行，n为列");Sys
在CUDA中优化矩阵转置
https://dmacssite.github.io/materials/MatrixTranspose.pdfhttps://dmacssite.github.io/materials/MatrixTranspose.pdf Chapter 1. Introduction 矩阵转置优化CUDA内存管理 本文档讨论了CUDA应用程序性能的各个方面，这些方面与有效使用GPU内存和应用于矩阵
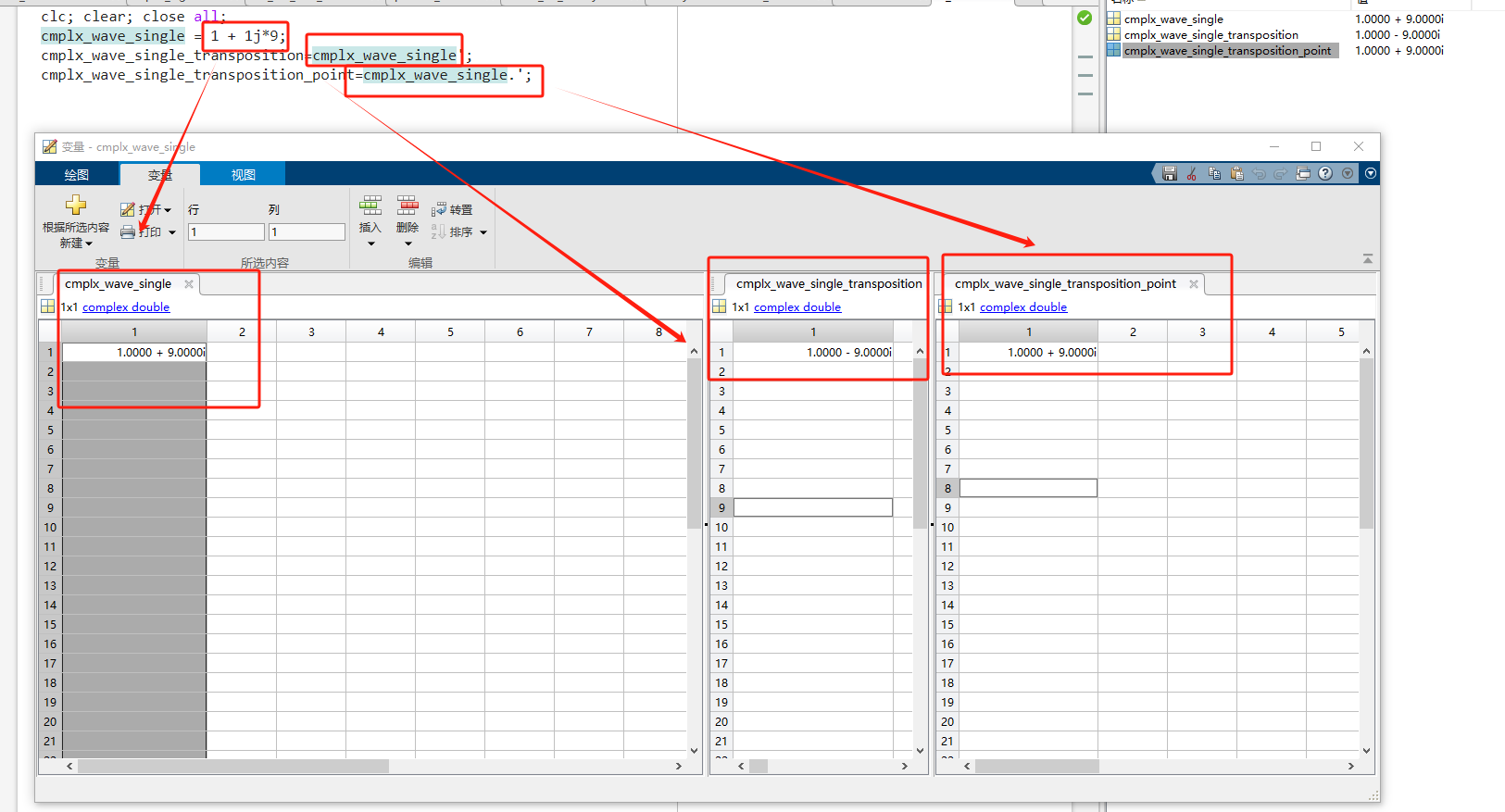
使用matlab的大坑，复数向量转置！！！！！变量区“转置变量“功能（共轭转置）、矩阵转置（默认也是共轭转置）、点转置
近期用verilog去做FFT相关的项目，需要用到matlab进行仿真然后和verilog出来的结果来做对比，然后计算误差。近期使用matlab犯了一个错误，极大的拖慢了项目进展，给我人都整emo了，因为怎么做仿真结果都不对，还好整体的代码都是我来写的，慢慢往下找就找到了问题的来源，全网没有看到多少人把这个愚蠢的错误写出来，我来引入一下。 代码错误的表现：复数向量的虚部被取反，正数变成负数，负数
一文让你看懂转置卷积（反卷积，分数卷积），非常详细的图解描述
点击上方“AI公园”，关注公众号，选择加“星标“或“置顶” 作者：Naoki Shibuya 编译：ronghuaiyang 导读 如果你听说过转置卷积并对它的实际含义感到困惑，这篇文章就是为你写的。 如果你听说过转置卷积并对它的实际含义感到困惑，这篇文章就是为你写的。 上采样的需求 当我们使用神经网络来生成图像的时候，通常需要从低分辨率的图像上采样成高分辨率的图像。 有很多的方
矩阵---A的行列式的值与A的转置的行列式的值是一致的
假设对A逐次进行行变换 这也就相对于A的转置来说,逐次进行相应的列变换 这也就意味着,A的行列式与A的转置的行列式,他们的值,都是一致的 只不过我们是将他们横着看,还是竖着来看的问题
sql-行转列2(转置)
行转列的常规做法是，group by+sum(if())【或count(if())】 例题： 表table如下： DDateshengfu2015-05-09胜2015-05-09胜2015-05-09负2015-05-09负2015-05-10胜2015-05-10负2015-05-10负 如果要生成下列结果, 该如何写sql语句? DDate胜负2015-05-09222015-05-
数组_例题：将3行4列的数组转置成4行3列并反向输出
# include <stdio.h>int main(void){ int a[3][4] = {11,12,13,14,21,22,23,24,31,32,33,34}; int b[4][3]; int i, j; for(i=0; i<4; i++) //转置数组； for(j=0; j<3; j++) b[i][j] = a[j][i]; for(i=3; i>=0;
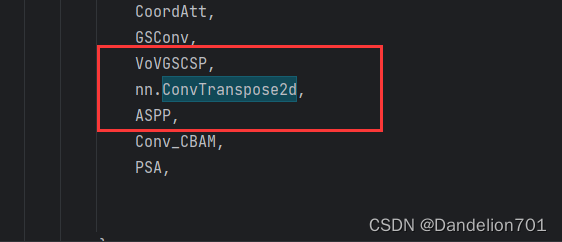
YOLOV5更换转置卷积，助力涨点！
由于转置卷积是nn库自带的，所以我们直接找到models文件夹中的yolo.py文件中的 parse_model函数，再在如下图的地方添加转置卷积模块 # YOLOv5 🚀 by Ultralytics, AGPL-3.0 license"""YOLO-specific modules.Usage:$ python models/yolo.py --cfg yolov5s.yam
2.3 单位矩阵和转置矩阵
声明：该文章翻译自MIT出版的《DEEP LEARNING》，博主会定期更新文章内容。由于博主能力有限，中间有过错之处希望大家给予批评指正，一起学习交流。 线性代数提供了一个强有力的工具 ——矩阵求逆，可以解决等式 Ax=b。 \boldsymbol{Ax}=\boldsymbol{b} 。 为了描述矩阵逆，我们首先需要定义单位矩阵的概念。当我们用单位矩阵乘以其它矩阵时，它不改变矩阵的值。我
矩阵转置 O(1)空间
题目：用O(1)的空间实现矩阵的转置 另外一篇文章：http://www.qushichao.com/archives/47.html 为了方便，使用一维数组来分析。所谓矩阵转置，行变列，列变行。在转置的过程中，有的元素位置是不变的；对于变化位置的元素，要求O(1)空间完成，那么这些位置的变化一定是有着规律的。 举例，2×5的矩阵，A={0,1,2,3,4,5,6,7,8,9
Python笔记：纯python处理矩阵：对矩阵进行转置
方法一 ：使用常规的思路 def transpose(M):# 初始化转置后的矩阵result = []# 获取转置前的行和列row, col = shape(M)# 先对列进行循环for i in range(col):# 外层循环的容器item = [] # 在列循环的内部进行行的循环for index in range(row):item.append(M[index][i])result
【深度学习理论】卷积神经网络的反卷积/转置卷积
卷积过程： 利用卷积核与覆盖的区域进行内积操作（就是对应元素相乘求和） 反卷积过程： 原名叫做反卷积，但是并不是很合理，所以转置卷积更合理一点。具体过程如下： （1）首先将卷积与感知野的乘积转换一下，将4*4的卷积核转换为下面的矩阵，然后4*4的原始数据转换为16*1的向量，这样子下面的矩阵一共有四行对应了四次卷积运算，0则表示在实际卷积过程中，卷积核与原图不重叠的位置。 （
计算图中反向传播求导权重矩阵需要转置的说明
在计算图中，基于链式法则的计算图反向求导是模型训练的关键算法，下面用图例说明为什么反向传播的时候，权重矩阵需要转置 按着图中箭头方向“从左向右进行计算”称为正向传播,即从计算图的出发点到结束点的传播, “从右往左计算”称为反向传播. 另一个例子: 当反向传播进来的是误差对上一层的导数时，反向传播矩阵使用正向传播矩阵的转置. 结束！
去雾笔记-Pixel Shuffle，逆Pixel Shuffle，棋盘效应，转置卷积
文章目录 1.Pixel Shuffle2.Inverse Pixel Shuffle3.棋盘效应4.转置卷积5.宽激活块6.PSPNet7.反射填充层（Reflective Padding Layer）8.tanh层 1.Pixel Shuffle Pixel Shuffle是一种用于图像超分辨率的技术，它通过重新排列图像的像素来增加图像的分辨率。具体来说，Pixel Shuf
10,09_维度变换,view、reshape,unsqueeze,Squeeze,expand,repeat,矩阵转置,transpose维度交换,permute,Broadcasting
1.9.Tensor维度变换 1.9.1.view、reshape 1.9.2.unsqueeze 1.9.3.Squeeze 1.9.4.expand 1.9.5.repeat 1.9.6.矩阵转置 1.9.7.transpose维度交换 1.9.8.permute 1.10.Broadcasting 1.9.Tensor维度变换 1.9.1.view、reshape 1.两者功能一样：将
矩阵分块转置降低 cache miss分析 （Cache Lab PartB）
Lab中给出的cache规格为： s=5, E=1, b=5 矩阵A和B在内存中连续存放。 Lab要求分别对32 * 32 ， 64 * 64， 61 * 67的矩阵做转置优化，用到的都是将矩阵分块分别转置的方法。相较于普通转置，为什么分块能够优化cache miss次数？ 分块是通过什么来实现优化的 — > 通过减少B一次访问的行数。 最根本的原因在于： Cache不能够一次装满整个矩阵，以最
用三元组存储稀疏矩阵并实现转置
基本概念 在学习线性代数的时候，经常用到矩阵。在C语言中，表示矩阵的最直观形式就是二维数组。然而在实际应用中，很多高阶矩阵中的非零元素非常少，这个时候如果继续使用二维数组存储，那么就会浪费很多存储空间。 在数据结构中，我们用三元组存储稀疏矩阵。三元组定义为(i,v,j)，这三个值一次表示矩阵的行、列、值。 有了基本的概念之后，就可以定义数据结构了 定义一个结构体，来表示三元组的基