本文主要是介绍2.3 单位矩阵和转置矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
声明:该文章翻译自MIT出版的《DEEP LEARNING》,博主会定期更新文章内容。由于博主能力有限,中间有过错之处希望大家给予批评指正,一起学习交流。
线性代数提供了一个强有力的工具 ——矩阵求逆,可以解决等式 Ax=b。
为了描述矩阵逆,我们首先需要定义单位矩阵的概念。当我们用单位矩阵乘以其它矩阵时,它不改变矩阵的值。我们用 In 表示n维单位矩阵。正式地,
∀x∈Rn,Inx=x.
单位矩阵的结构很简单:沿着主对角线的元素都是1,而其它元素都是0。如下图:
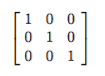
A 的逆表示为 A−1 ,并且满足条件:
A−1A=In.
现在我们可以通过下面的步骤解决等式2.1:
Ax=b
A−1Ax=A−1b
Inx=A−1b
x=A−1b
当然,这依赖于
A−1 。在下一节,我们将讨论
A−1 存在的条件。
当 A−1 存在时,有几种不同的算法可以在闭合式(closed form)中找到它。理论上,对于不同的 b 值,可以用同样的逆矩阵求解。然而, A−1 作为理论工具有用,但实际中的许多软件应用不应该使用它。因为在数字计算机上 A−1 只能表示有限的精度,而充分利用 b 值的算法通常可以得到 x 更精确的估计值。
这篇关于2.3 单位矩阵和转置矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




