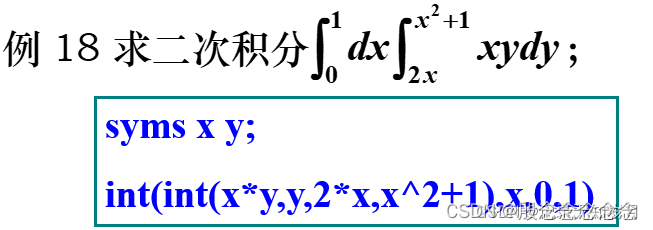高数专题
高数函数的连续性与间断点
这几天做的真题中涉及到的函数的连续性和间断点的题也不少,而且正确率不高,下面总结一下这部分知识。 【知识点】 一、连续性 所谓连续,顾名思义,下面有两种定义方法: (1) 该定义主要是用于证明题,考查逻辑推理问题。 (2)设函数f(x)在点X0的某一领域内有定义,且有x->时,f(x)的极限等于f(
【高数】三角函数积累
1.两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1
【MATLAB】(高数)
参考文章 函数极限 导数与偏导 极值和最值 局部范围的最值 局部范围内的最值,相当于函数的极值 离散数据的最值 多元函数的极值 fminunc [x, fval] = fminunc(fun, x0) fun为代求极值的函数;x0为起始点,即从这个点开始寻找极值,由于该函数用于无约束的多元函数极值问题 fmincon [x, fval] =
人工智能的数学基础(高数)
🌞欢迎来到人工智能的世界 🌈博客主页:卿云阁 💌欢迎关注🎉点赞👍收藏⭐️留言📝 🌟本文由卿云阁原创! 📆首发时间:🌹2024年5月29日🌹 ✉️希望可以和大家一起完成进阶之路! 🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢! 🙏本书是自己写的哦,因为编辑太麻烦啦,就粘贴了图片,如果需要电子版的可以私信哈。 目录 数列 数列与递推关系式 数列极限 累加 函数
AI算法-高数5.1-线性代数-向量间的关系
宋浩老师: 3.2 向量间的线性关系(一)_哔哩哔哩_bilibili 向量间的关系: 判断向量贝塔(β)是否是阿尔法(α)的线性组合,按如上转化成方程组,方程组有解是线性组合,没解就不是,如下图。
AI算法-高数5-线性代数1-基本概念、向量
线性代数:主要研究1、张量==>CV计算机视觉 2、研究张量的线性关系。 深度学习的表现之所以能够超过传统的机器学习算法离不开神经网络,然而神经网络最基本的数据结构就是向量和矩阵,神经网络的输入是向量,然后通过每个矩阵对向量进行线性变换,再经过激活函数的非线性变换,通过层层计算最终使得损失函数的最小化,完成模型的训练。所以要想学好深度学习,对这些基础的数据结构还是要非常了解。 一、基本概念:
AI算法工程师课程学习-数学基础-高数1-微积分
机器学习数学基础学习路线:1.高中数学-->大学2.微积分-->3.线性代数-->4.概率论-->5.优化理论。 为尽快进入到AI算法课程的学习,现在高数的学习要求: 1.看得懂,知道是什么,能听得懂,能理解讲的是什么;2.会查资料,例如通过市面上相关的AI工具来计算(省时省力),我也是第一次学AI算法工程师,我将数学基础部分的学习都记录下来,希望对走同样路的小伙伴们有些帮助。 1.微积
【考研高数】学习笔记分享
派大星说数学(导学部分) 关于做题 测试 答疑阶段 直播 群内 高中基础知识导学 一、数与式 述了课程学习和因式分解、分式拆解等知识点。学生应了解课程内容,带着疑问听课,不要抄笔记,导学课和基础课都有测验,定期答题并上传过程,会有批改。跟学课程难度不大,放心学习。在因式分解方面,视频介绍了如何将假分式拆成多项式和真分式,强调了分母的因式分解是处理真分式的第一步。处理假
考研高数(对比一元微分学和一元积分学概念)
1.一元微分学的概念和一元积分学的概念 一元微分 1.导数 函数一点可导的充要条件:左右导数均存在且相等(也可说左右极限存在且相等) 函数一点可导的必要条件:若f(x)在一点可导,则f(x)在该点连续。反之未必。 2.导数的几何意义 函数y=f(x) 在x=x0处的导数 f′(x0),表示曲线y=f(x)在点P(x0,f(x0))处的切线的斜率k。 注意:一点的导数存在-->
第三章:00023工本高数第二章多元函数的微分学考点
1.考点一:一元极限基础知识 不考一元极限,但作为基础知识必不可少 1.了解运用两个重要极限 1. lim x → 0 s i n x x
考研数学——高数:高斯公式
助记: 关于积分时什么时候可以将变量整体代入积分式的问题:在积分过程中,如果某一整体恒为常量,则可以直接替换为定值,常见于对线或面的积分。 而在这题,用高斯公式之前是面积分,如果有这个整体出现的话是可以带的,但是用了高斯公式之后是属于重积分,是对一个球体进行积分,而在积分过程中x²+y²+z²≤R²,不是恒等式,所以代入肯定是有问题的。
Python数值微积分,摆脱被高数支配的恐惧
文章目录 差分和累加积分多重积分 Python科学计算:数组💯数据生成 差分和累加 微积分是现代科学最基础的数学工具,但其应用对象往往是连续函数,而其在非连续函数的类比,便是差分与累加。在【numpy】中,可通过【diff】和【cumsum】来完成这两项任务。 以 y = sin 2 x y=\sin 2x y=sin2x为例,其导数为 d y d x = 2 cos
专升本高数定理及性质集锦
专升本高数定理及性质集锦 1.数列极限的存在准则2.数列极限的四则运算定理3.极限的充要条件4.函数极限的定理5.无穷小量的基本性质6.等价无穷小量代换定理7.两个重要极限8.函数在一点处连续的性质9.闭区间上连续函数的性质10.零点定理11.初等函数的连续性12.可导与连续的关系13.导数的计算14.微分的计算15.微分形式不变性16.定积分的基本性质17.变上限定积分求导定理
考研数学——高数:多元函数微分法及其应用
因为复习阶段全篇很细节的写下来一来比较费时间,二容易导致为了记笔记而记。 接下来的内容只会保留上课中比较有意义的地方,以及有自己助于理解的想法 全微分 助记: 证明是否可微,首先判断两个偏导数是否存在,不存在则直接否定; 若存在,则接着利用可微的定义中(A为对x的偏导,B为对y的偏导,ρ为 ) 代入后表示为高阶无穷小的形式(相除极限趋于0)即可证明 助记: 由两
考研数学——高数:不定积分
一、换元定积分法 ①第一类换元法 定理1 若 则 这个方法也叫凑微分法,实际运用中是将被积函数的一部分拿到d的后面(相当于对部分求积分)然后将d之后的部分看成一个整体,再对原函数积分,起到化简的效果 例题(求下列不定积分) ②
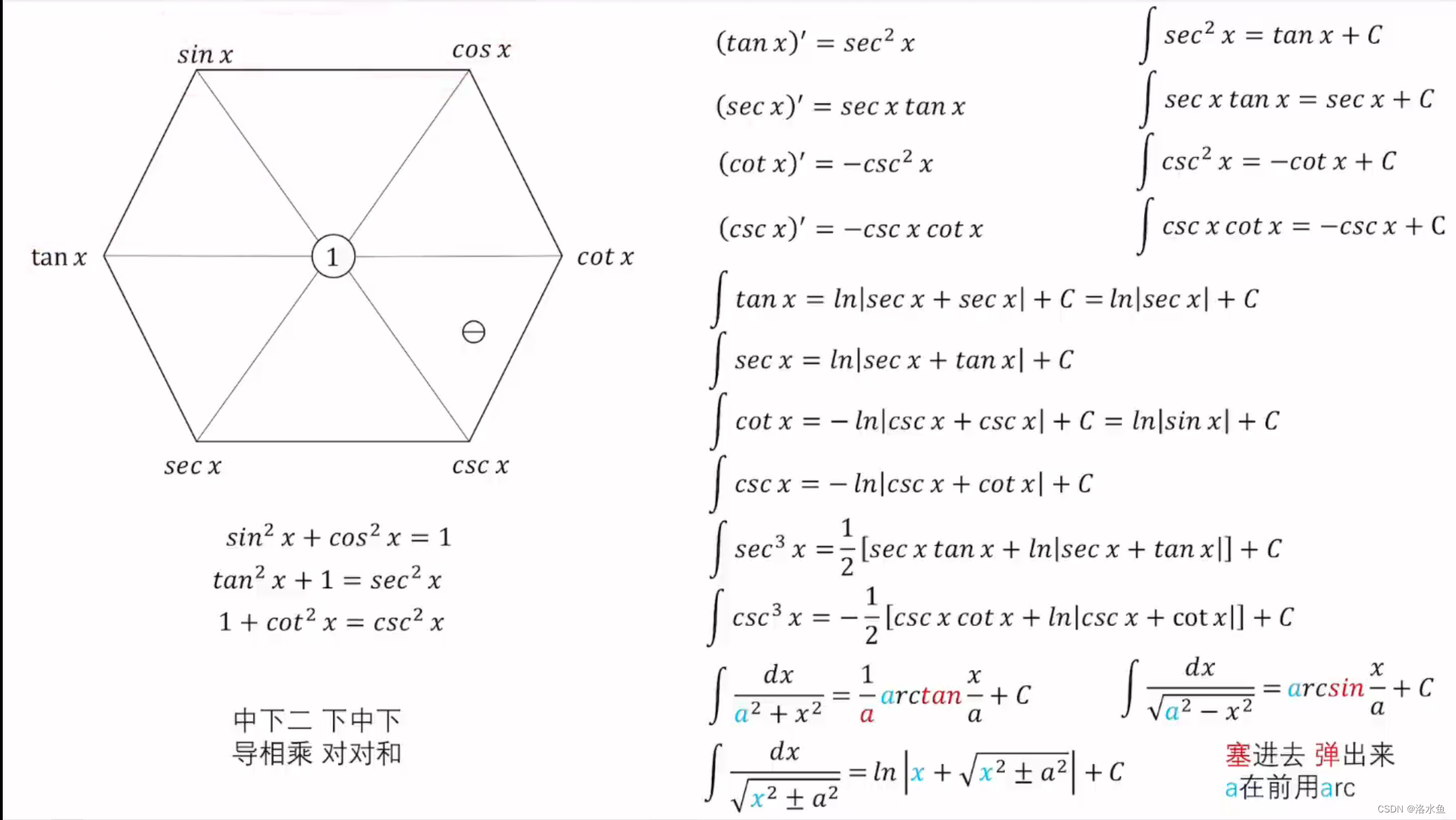
高数考研 -- 公式总结(更新中)
1. 两个重要极限 (1) lim x → 0 sin x x = 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}=1 limx→0xsinx=1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) = 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)