本文主要是介绍【考研高数】学习笔记分享,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
派大星说数学(导学部分)
关于做题

测试

答疑阶段
-
直播
-
群内
高中基础知识导学
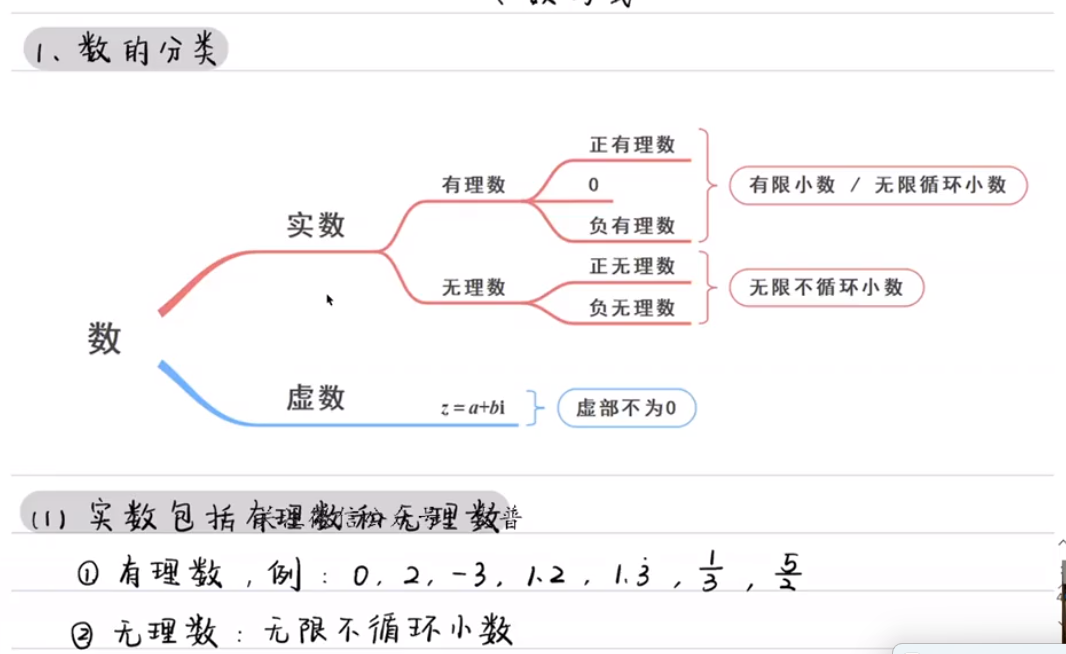
一、数与式
述了课程学习和因式分解、分式拆解等知识点。学生应了解课程内容,带着疑问听课,不要抄笔记,导学课和基础课都有测验,定期答题并上传过程,会有批改。跟学课程难度不大,放心学习。在因式分解方面,视频介绍了如何将假分式拆成多项式和真分式,强调了分母的因式分解是处理真分式的第一步。处理假分式时,不能拆成真分式。







长除法—试根法




待定系数法

裂项求待定系数,下面是x-1(x-2)(x-2)**直接弄成三项消去
有时候最傻的方法才是最聪明的方法。
二、代数
六种初等函数
- 常数函数
- 幂函数
- 指数函数
- 对数函数
- 三角函数
- 反三角函数

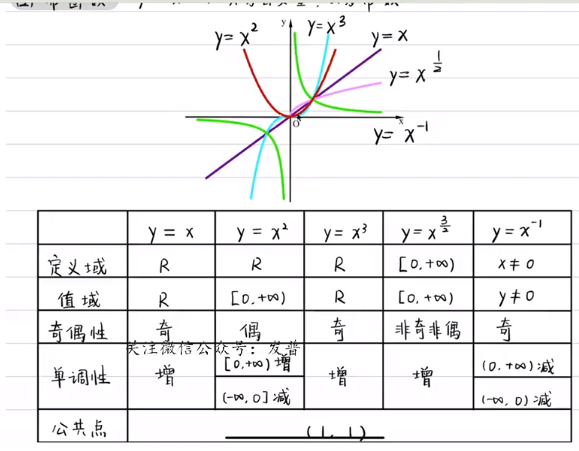
注意点
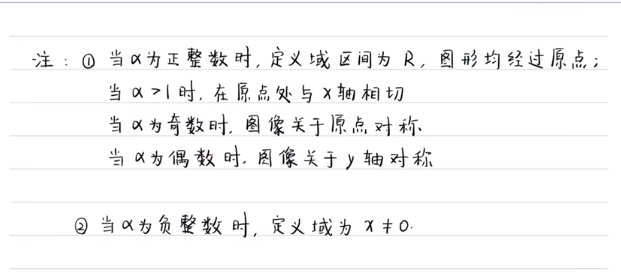
指数函数
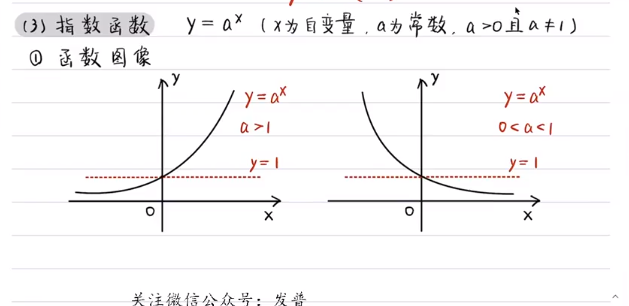
都经过(0,1)点


对数函数:

常用对数函数:

对数函数图像:
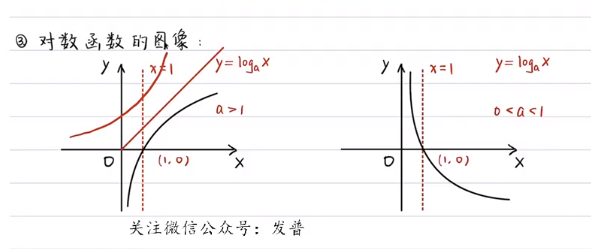
性质


换底公式(不常考)

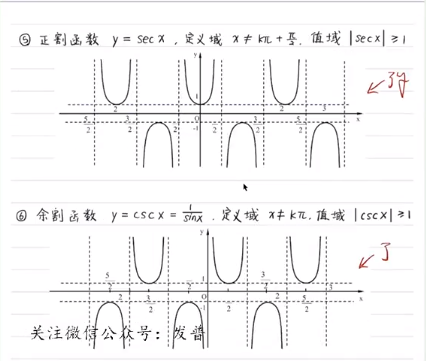
三角函数

记住c和s是一对的倒数关系。

函数图像:
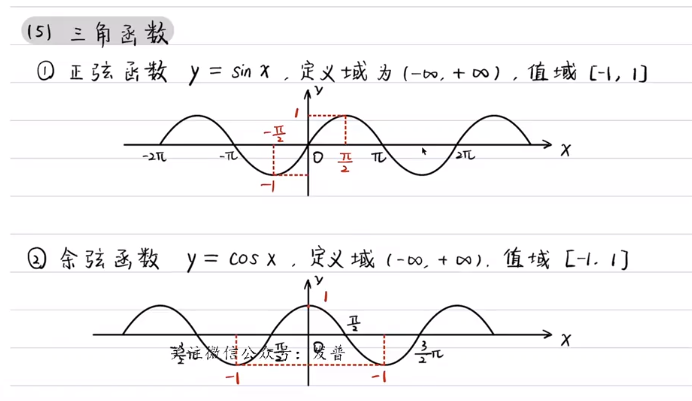
三角函数的性质

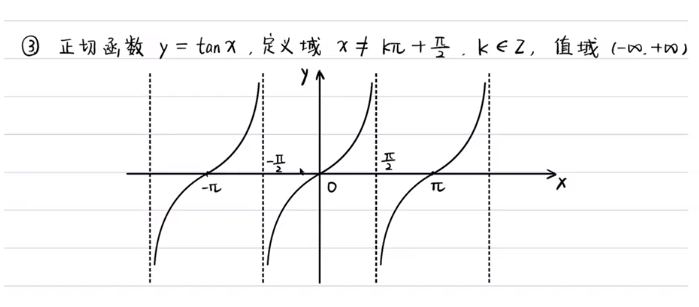
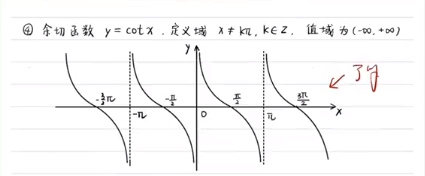

反函数的理解
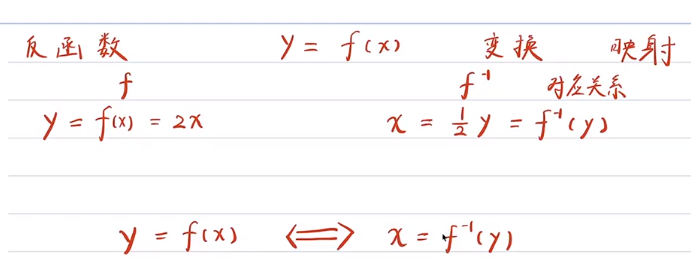
关于y=x对称
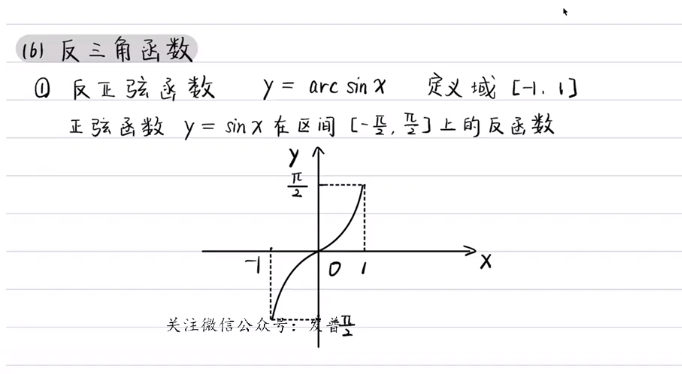
一一对应的关系函数才存在反函数。acsinx就是认为缩短区间
KaTeX parse error: Undefined control sequence: \matrix at position 23: …osx a = \left[ \̲m̲a̲t̲r̲i̲x̲{ \alpha_1 & …
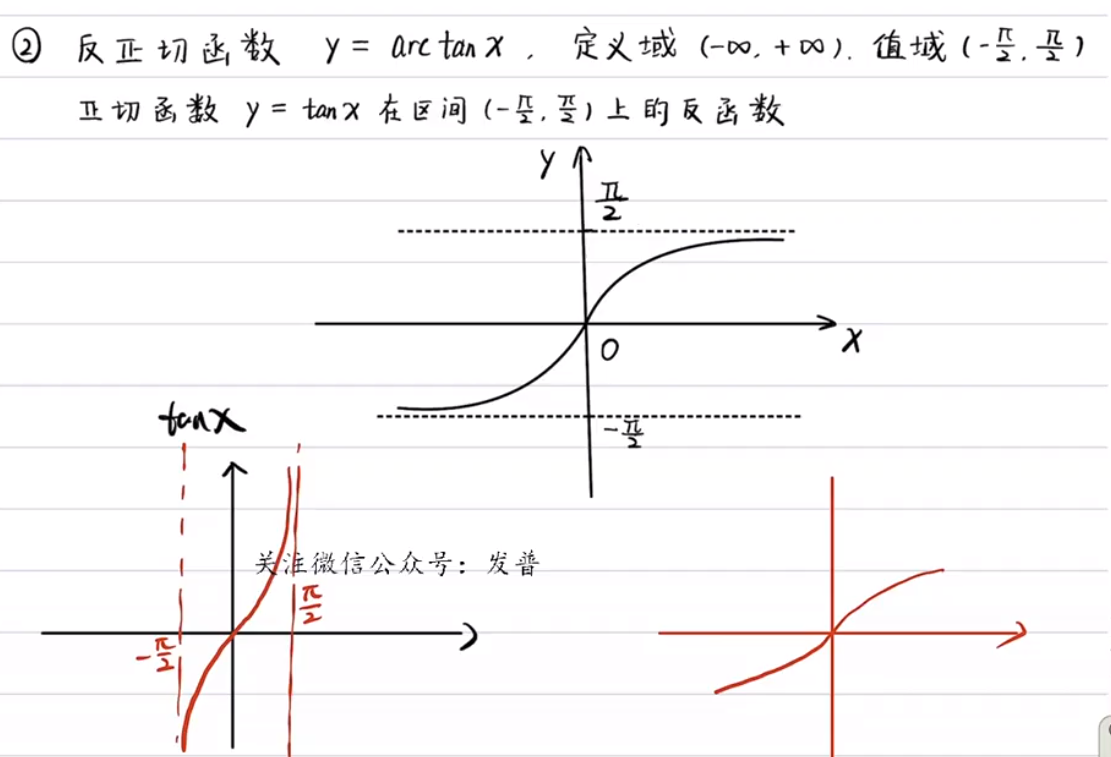
三角函数公式:


补充
诱导公式

奇数变偶不变




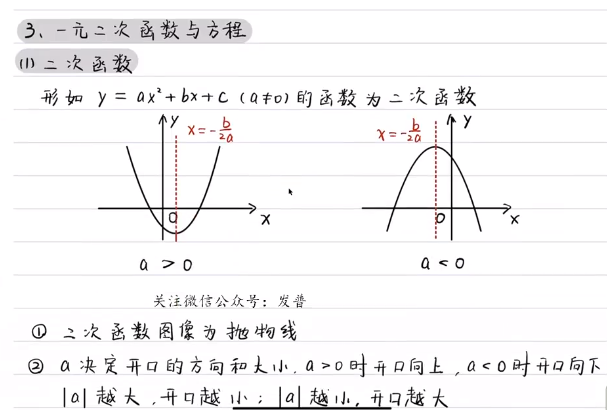

数形结合
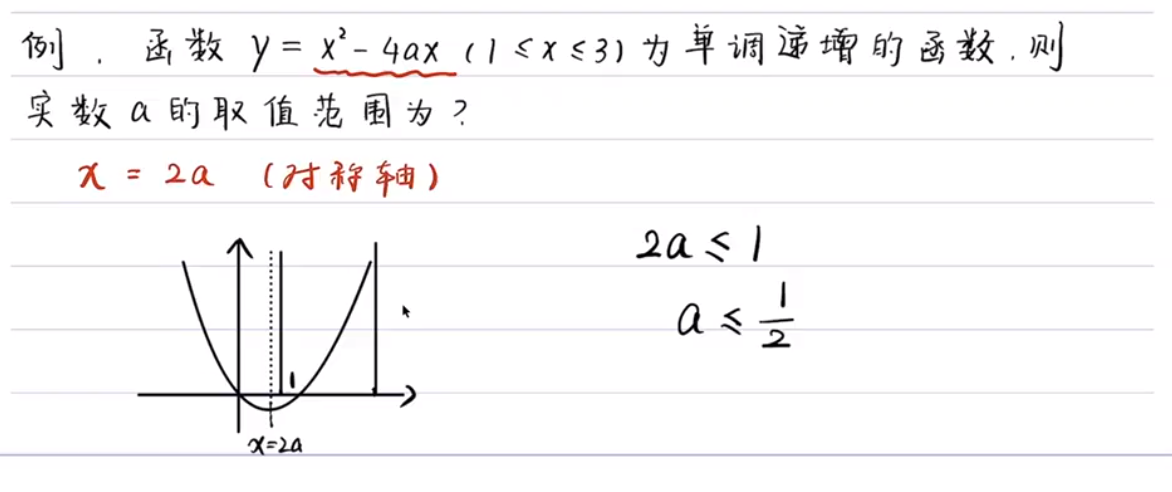




韦达定理例题

不要跳步骤!!!

注意检查
数列






等比数列
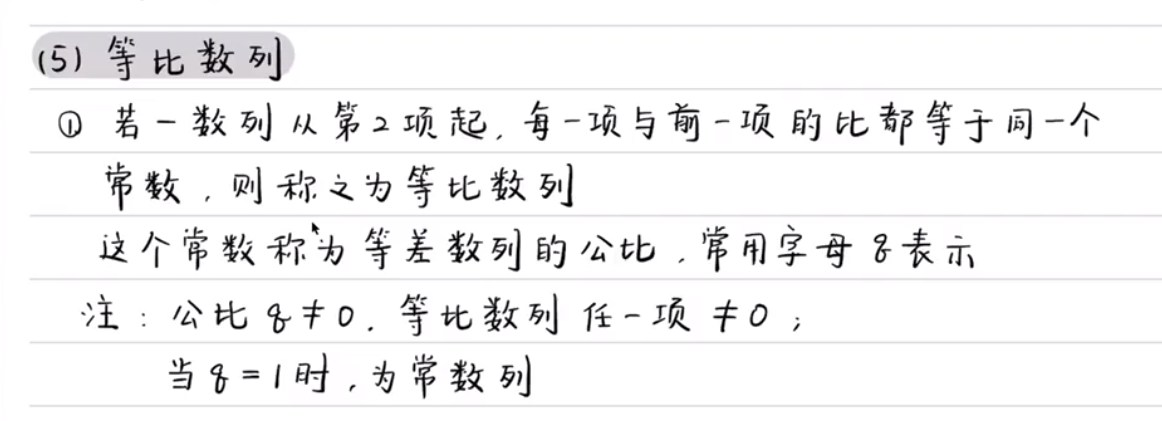




三、几何
来
- 平面几何
- 立体几何
- 解析几何
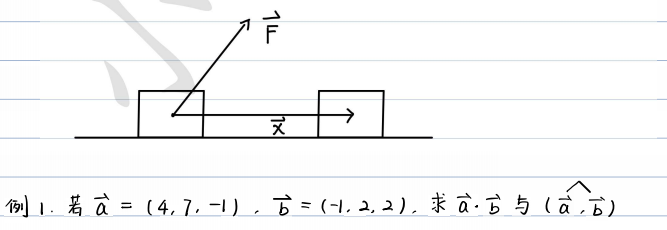
- 向量解析
平面几何

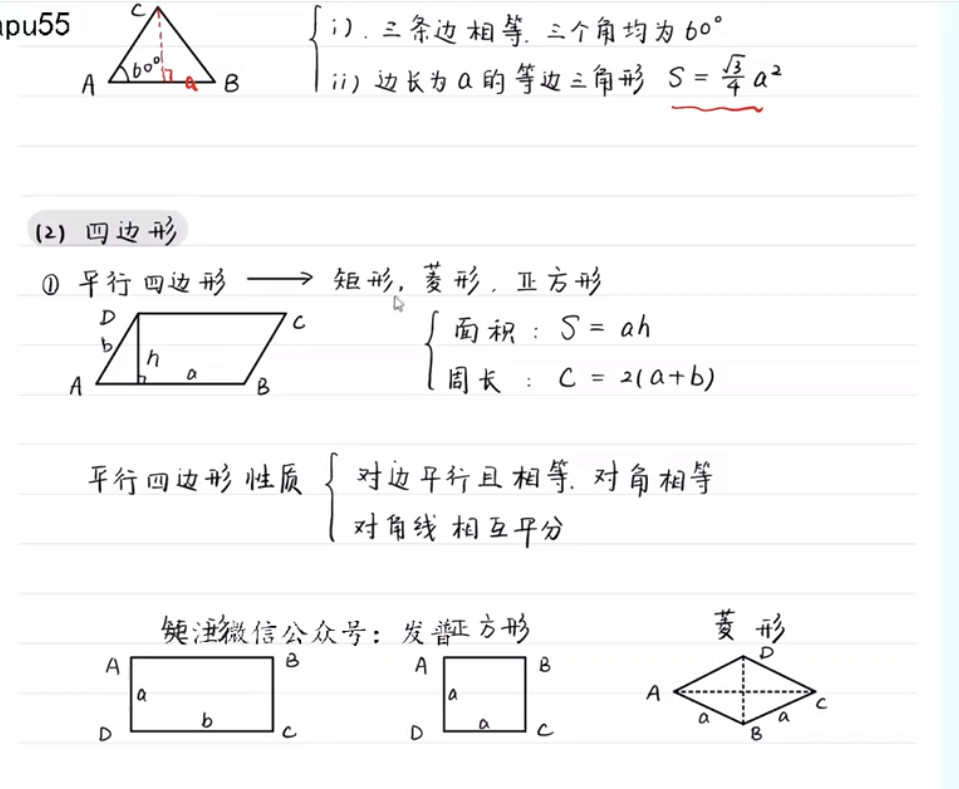
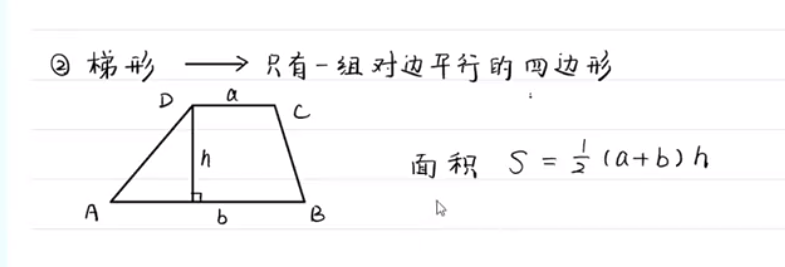



立体几何
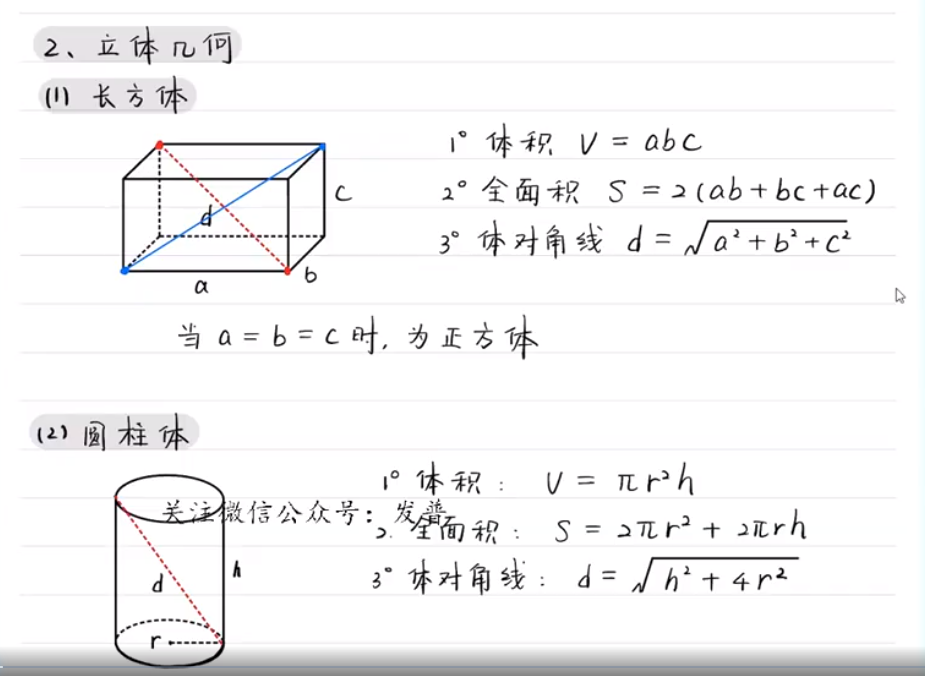
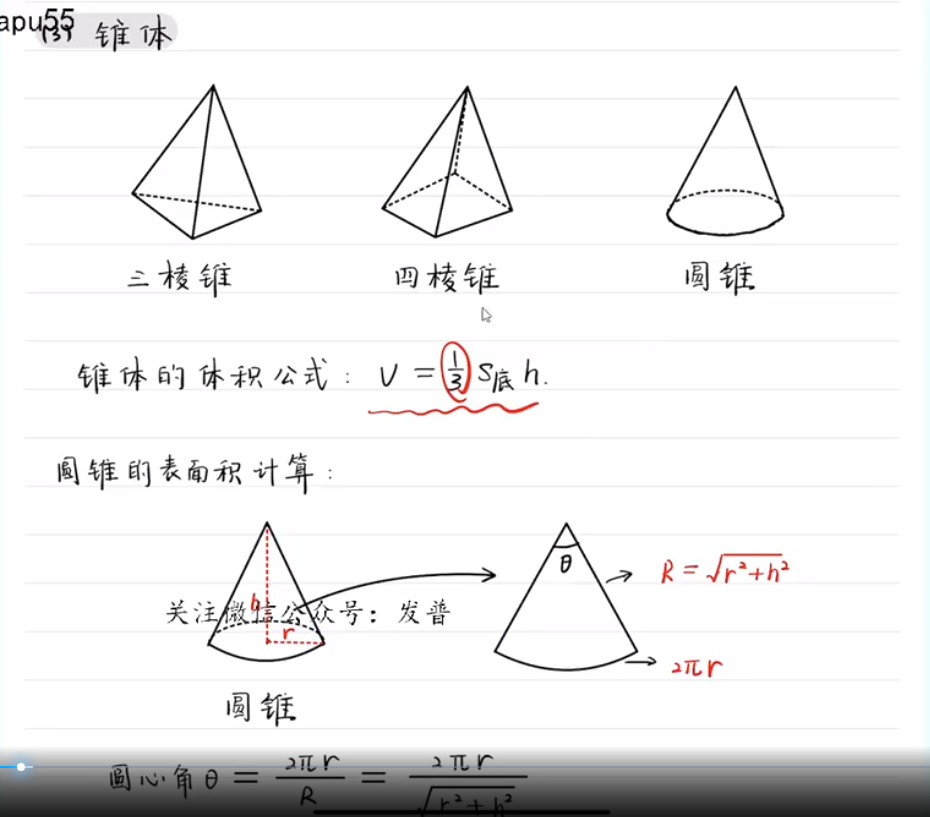
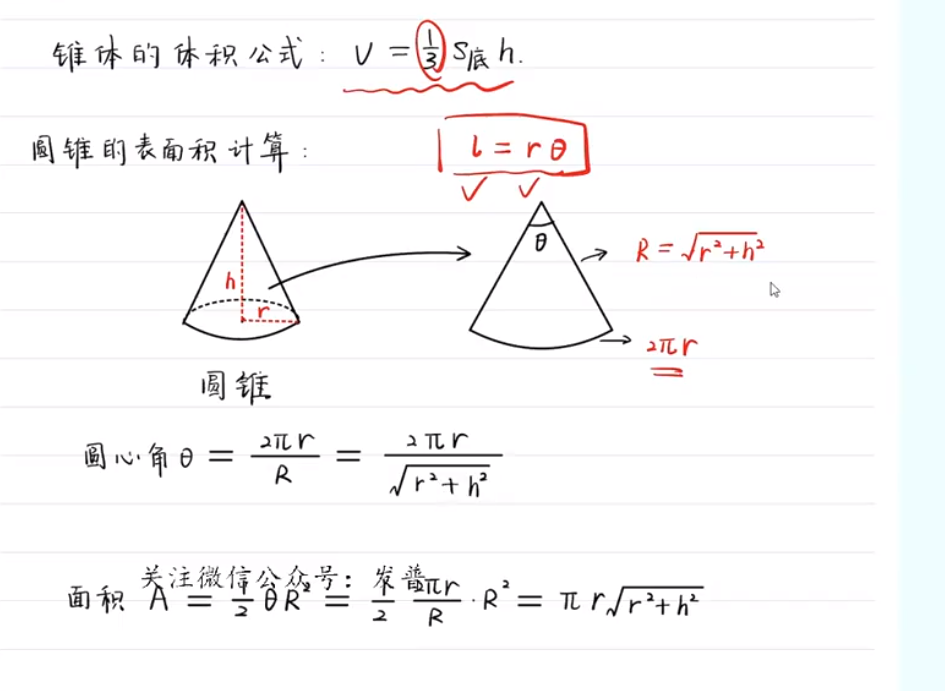
圆台
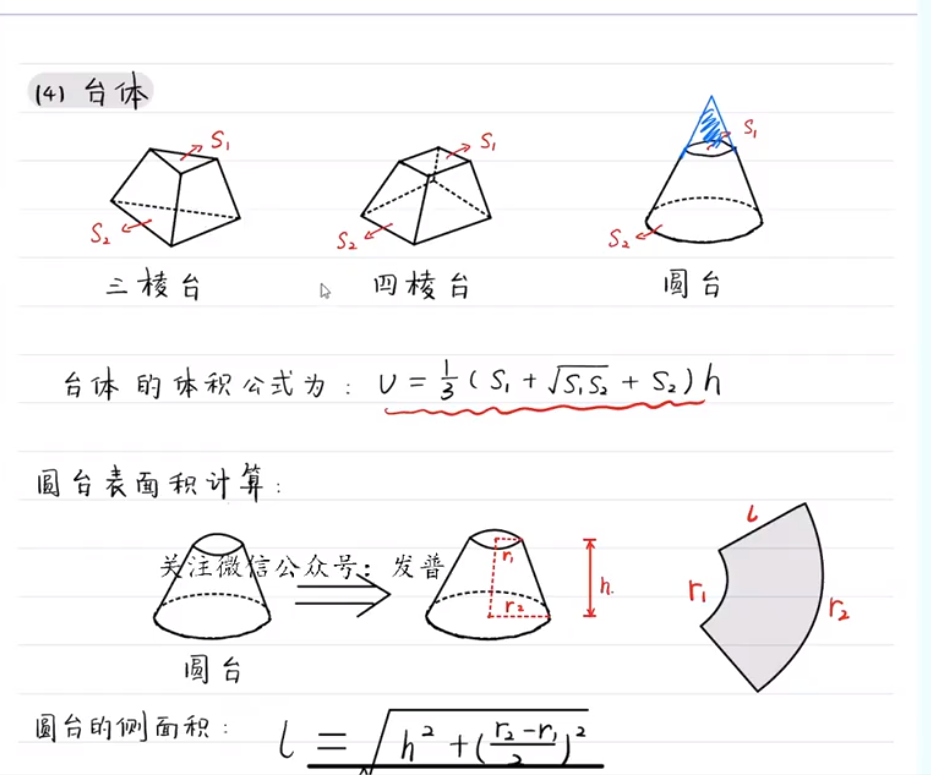

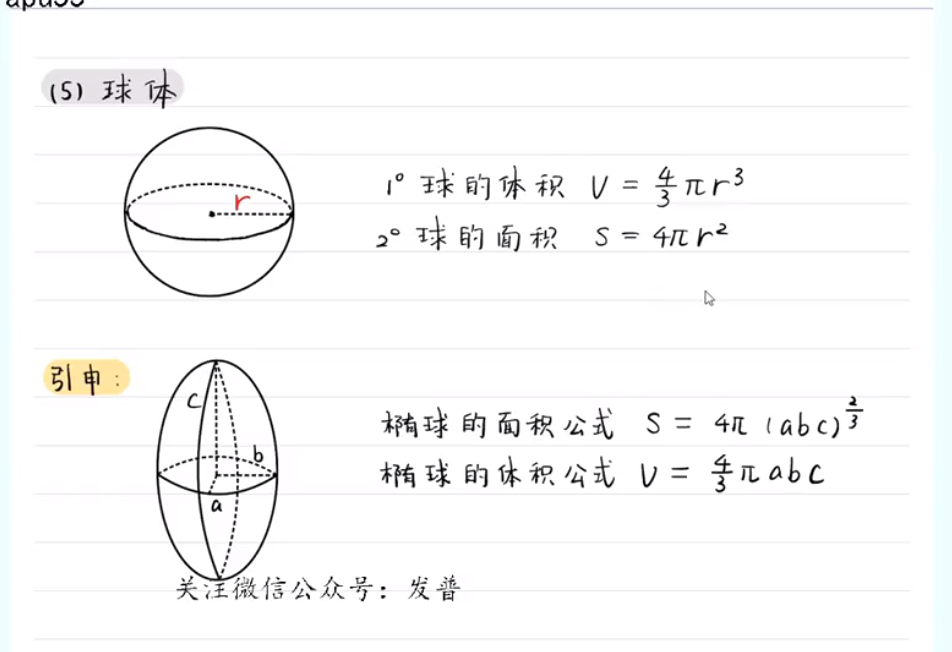



解析几何
笛卡尔直角坐标系



二者转换
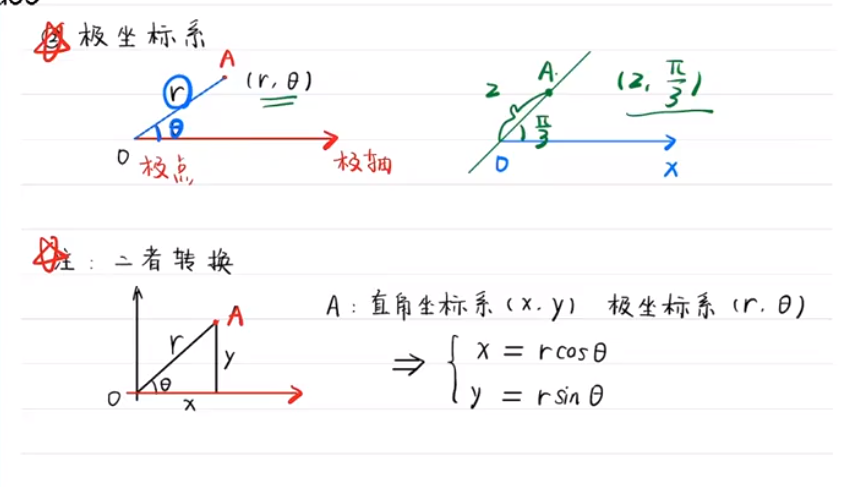
常见的极坐标系曲线


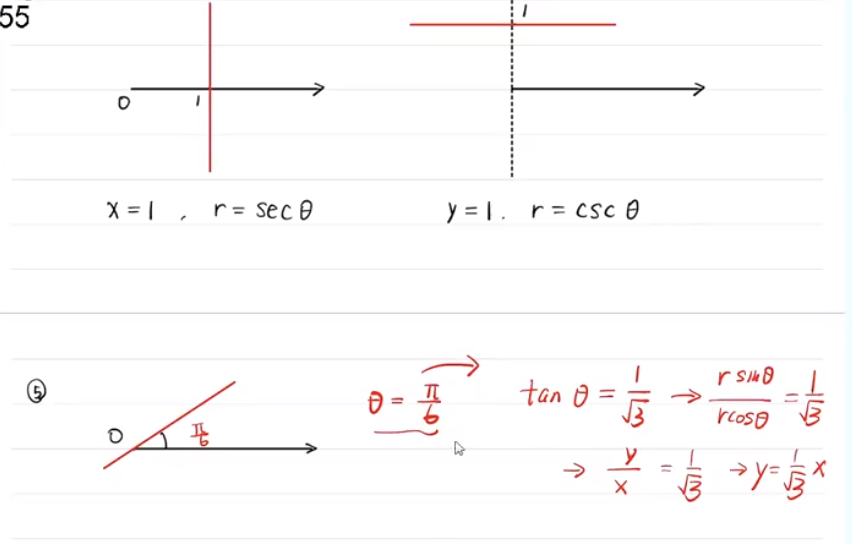


描点法
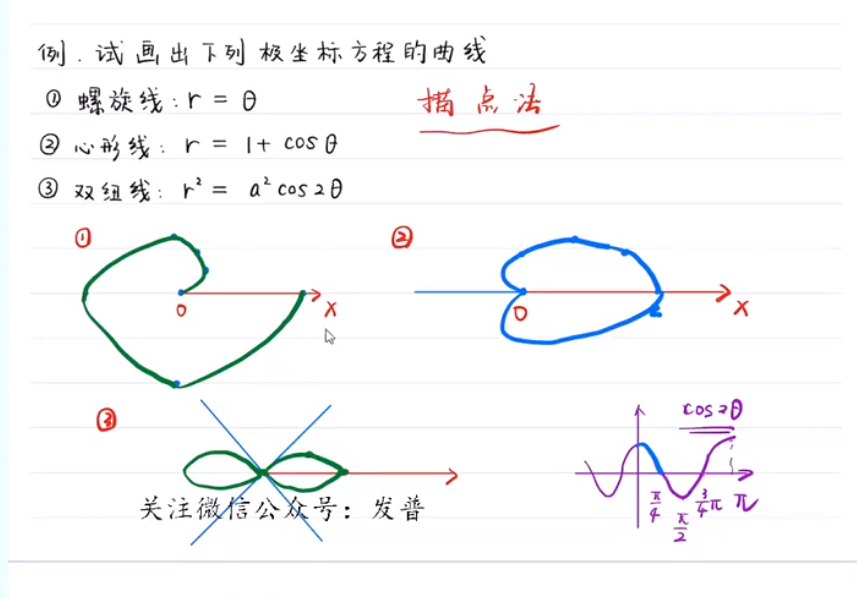

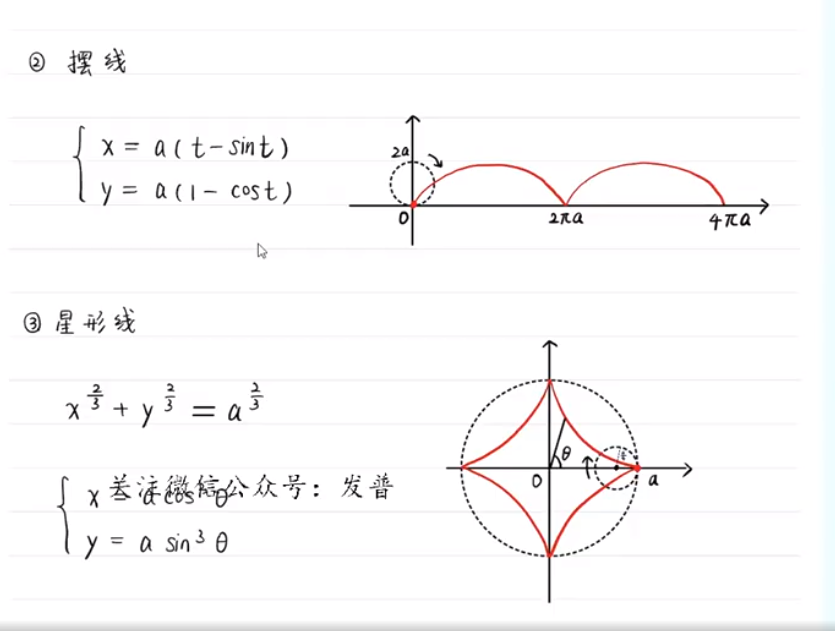
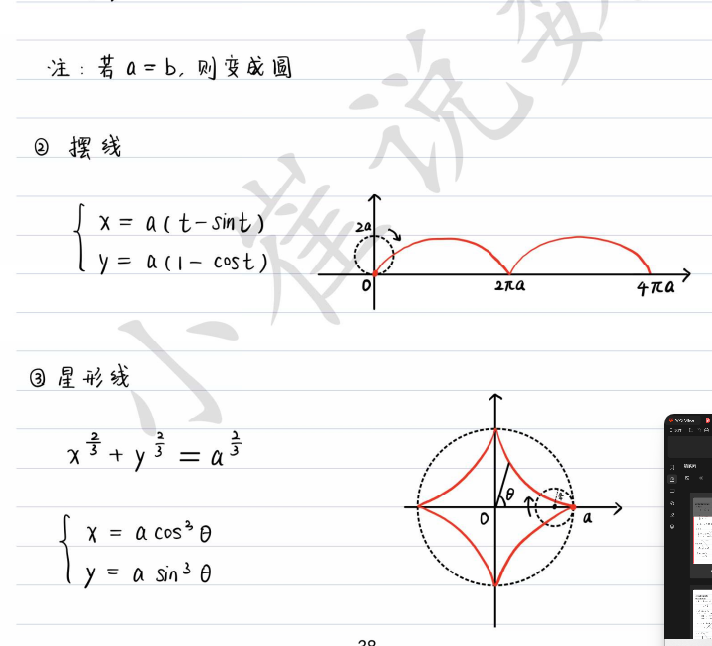
摆线






这篇关于【考研高数】学习笔记分享的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




