着色专题

回溯法-图的m着色问题

图的 m 着色问题问题描述给定一个无向连通图 ( G = (V, E) ) 和 ( m ) 种颜色，我们的任务是为图 ( G ) 的每个顶点着色，使得相邻的顶点颜色不同。如果存在这样的着色方案，我们称之为图 ( G ) 的 ( m ) 可着色问题。算法思路初始化：创建一个二维数组 colors 来记录每个顶点的颜色。选择起始点：从图中任选一个顶点作为起始点，并为其着色。相邻顶点着色

1079: [SCOI2008]着色方案（dp之记忆化搜索）

题目链接题意：略解答：考虑到每种颜色最多只能涂5个，设dp[a][b][c][d][e][last]：能涂一个格子的颜色有a种，能涂2个格子的颜色有b种，能涂3个格子的颜色有c种，能够涂4个格子的颜色有d种，能够涂5个格子的颜色有e种，且上一次涂的是last，的方案数。能够想到的是，比如一种颜色x能涂3个格子，当我们使用它涂一个格子后，那么它就会变为能涂2个格子的类别中去了。这一点决定

通过MindOpt APL建模求解组合优化问题中的常见问题：图着色问题

组合优化问题：图着色问题通过MindOpt APL建模求解组合优化问题中的常见问题：图着色问题 1. 背景知识 1.1. 组合优化问题在之前发布的《组合优化问题：装箱问题》中，我们讲解了什么是组合优化（Combinatorial Optimization，CO）。这里仅简述： “组合”指的是从有限的对象集合中选择其中一部分元素作为解的过程，而“优化”则指的是在满足一定条件下，使得

如何为 Polar DataFrame 着色

继续使用 Polars 库，同时能够为表格添加颜色和样式本文中的示例展示了 Polars 表格在样式调整前后的对比欢迎来到雲闪世界。自 2022 年 Polars 库发布以来，它作为超高速 DataFrame 库迅速流行起来。与 Pandas 相比，白熊经过测试，速度更快。根据Polars 官方网站的说法，它声称性能提升了 30 倍以上。然而，没有什么是

日撸Java三百行（day35：图的m着色问题）

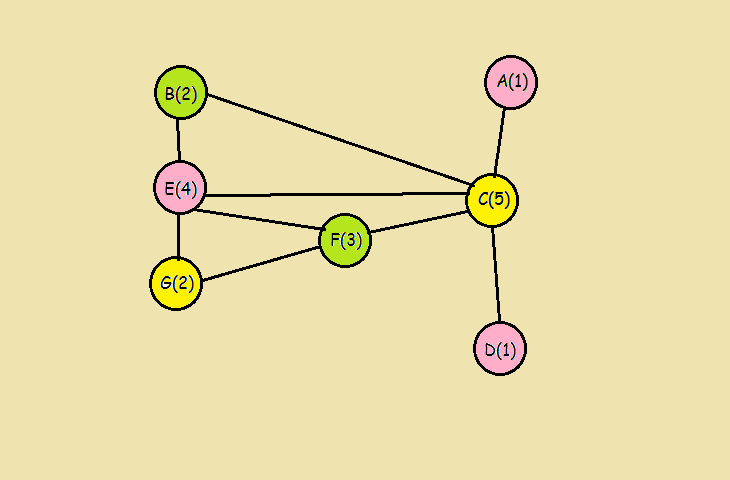
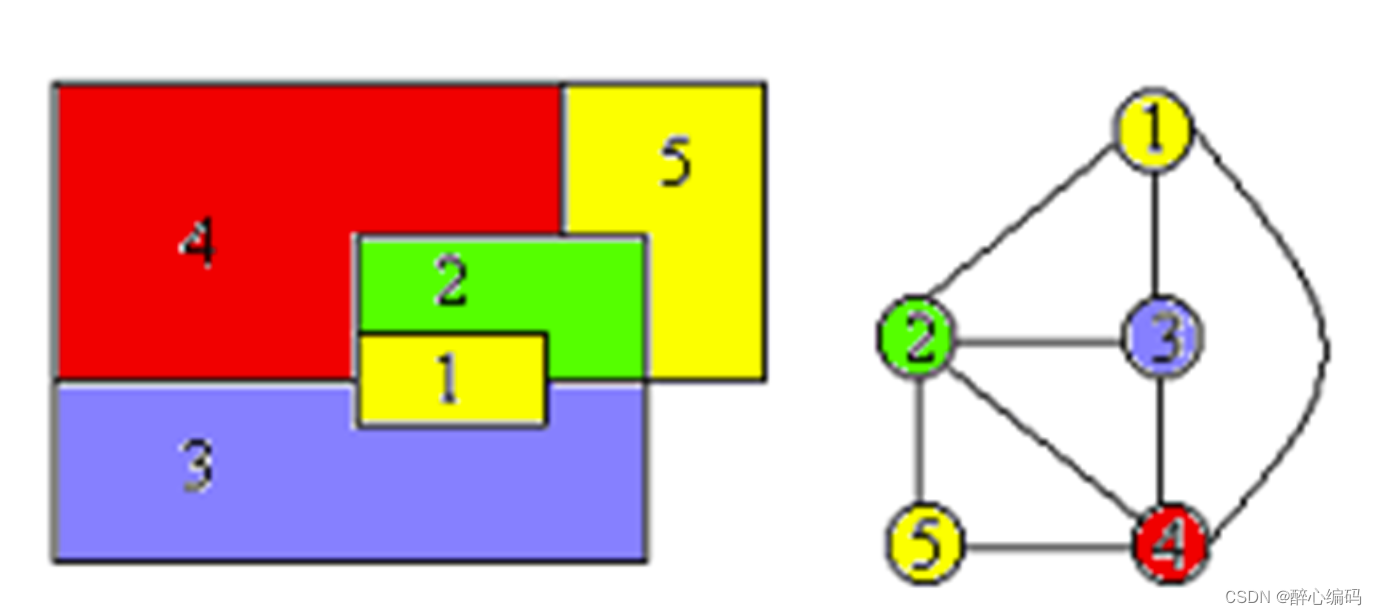
目录一、问题描述二、思路分析三、代码实现总结一、问题描述在高中学习排列组合的时候，有一个非常经典的问题，就是涂色问题，即用m种颜色给n块区域涂色，要求每块区域只能涂同一种颜色且相邻区域的颜色不能相同，问一共有多少种涂色方案。还记得当时自己是怎么做的吗？下面我们就用一个具体的例子来回顾一下。如下图，共有A、B、C、D四块区域，用五种颜色给它们涂色，要求每块区域只能

语法没错，vim却有时不着色（高亮显示）的原因

linux下vim编辑器，在编辑文件时，明明语法没有问题，有时候它能着色高亮显示，有时候就不行，这曾让我对linux的整体印象大打折扣。你遇到过吗？大家都是做软件的，应该明白这种完美主义心理。就比如设计一个软件，只要是正式发布的，我愿意让它“麻雀虽小五脏俱全”，可以功能不强大，可以不是最好看，但必须完整。安装是否容易顺畅挑环境？卸载是否顺畅不留垃圾？按F1是否能调出适宜的帮助手册？是否禁得起时

slab算法中着色[cachep-colour_off]的物理意义

Cited from http://www.sudu.cn/info/article/articleInfo.php?aId=291684 对于arm9处理器,当使用指令控制协处理器cp15打开数据缓存(DCache)时,arm9内部的数据总线上的数据就都会被缓存到arm9内部的物理cache中,对于arm9处理器at91rm9200来说,dcache大小为16k, 物理分布情况是这样的:

顶点着色技术在AI去衣中的作用

在当今的数字时代，人工智能（AI）已经渗透到我们生活的方方面面，从智能家居到自动驾驶汽车，再到在线购物推荐。然而，AI的影响远不止于此。近年来，AI在图像处理和计算机视觉领域的应用取得了显著进展，其中之一就是AI去衣技术。这种技术利用深度学习算法，可以在不侵犯隐私的情况下去除照片或视频中的衣物。在这个过程中，顶点着色技术发挥了关键作用。本文将探讨顶点着色技术在AI去衣中的作用。首先，我们需要了

【图论及其运用 — 电子科技大学】（七）第七章图的着色

一、图的边着色 (一)、相关概念定义1 给定图 G = ( V , E ) G=(V,E) G=(V,E)，称映射 π : E → { 1 , 2 , 3 , . . . , k } \pi : E \to \{1, 2, 3, ..., k\} π:E→{1,2,3,...,k} 为 G G G 的一个 k k k 边着色，简称边着色，称 { 1 , 2 , 3 , .

图表控件LightningChart .NET中文教程 - 创建3D网格模型实时着色应用

LightningChart.NET完全由GPU加速，并且性能经过优化，可用于实时显示海量数据-超过10亿个数据点。 LightningChart包括广泛的2D，高级3D，Polar，Smith，3D饼/甜甜圈，地理地图和GIS图表以及适用于科学，工程，医学，航空，贸易，能源和其他领域的体绘制功能。立即获取LightningChart.NET新版下载 3D网格模型实时着色应用程序在这个例

slab着色--一种必然认输的妥协

在最新的linux2.6.28内核当中已经不见slab着色的踪迹了，记得研究2.6.9的时候，我还为理解slab着色大伤脑筋，而实际上我当时根本没有理解它的设计初衷以及最终的效果，只是把它当成了一个纯粹的“算法”来玩，还玩得不亦乐乎... slab的目的是什么？其实它是为了在软件缓存和硬件缓存冲突的时候达成的一种妥协，而普遍的观点是只有相互平等的当事者才具有妥协的可能，如果关系根

【算法设计与分析】实验报告c++python实现(TSP问题、哈夫曼编码问题、顾客安排问题、最小生成树问题、图着色问题)

一、实验目的 1．加深学生对贪心算法设计方法的基本思想、基本步骤、基本方法的理解与掌握； 2．提高学生利用课堂所学知识解决实际问题的能力； 3．提高学生综合应用所学知识解决实际问题的能力。二、实验任务用贪心算法实现： 1、TSP问题 TSP问题（Travelling Salesman Problem）即旅行商问题，又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行

Qt_OpengGL：平面图形的着色渲染小测

Qt_OpengGL：平面图形的着色渲染小测 //.h #ifndef GLWIDGET_H#define GLWIDGET_H#include <QtOpenGL>#include <QWidget>class GLWidget : public QGLWidget{Q_OBJECTpublic

现代计算机图形学笔记（五）——深度测试、着色

可见性与遮挡(Z-buffering) 根据常识，我们很容易的想到画家在作画的时候如何体现遮挡。在作画时一般都是先画远处的物体，之后再画近处的物体，这样画出的画就可以体现出遮挡，该算法称为画家算法。画家算法需要先对所有物体的深度进行排序（最少需要 n log ⁡ n n\log n nlogn的时间复杂度），然后依次按顺序画在屏幕上（光栅化）。画家算法虽然思想简单，但并不能解决所有的遮挡

区间图着色问题：贪心算法设计及实现

区间图着色问题：贪心算法设计及实现 1. 问题定义2. 贪心算法设计2.1 活动排序2.2 分配教室2.3 算法终止 3. 伪代码4. C语言实现5. 算法分析6. 结论7. 参考文献在本文中，我们将探讨如何使用贪心算法解决一个特定的资源分配问题，即区间图着色问题。该问题可以描述为将一系列活动分配到最少数量的教室中，其中任意活动都可以在任意教室进行，但两个不兼容的活动不能安排在同一

基于贪心策略的，游戏战略地图着色算法设计（Unity）

一共有九种颜色，初始化有11个国家，所以相邻国家势必有颜色冲突的可能性（因为随着游戏进程国家有消失或新增的可能，因此不能写死），为此需要设计一种着色算法，因为游戏中的国家数量不会特别多，所以性能不是考虑的首要因素，因此采取贪心策略，最终算法时间复杂度为 O ( n 2 ) O(n^2) O(n2)。初始的游戏地图：将其抽象成无向图，存储国家间的邻近关系，如下：（国家序号从0到10：燕、晋

1079: [SCOI2008]着色方案（记忆化搜索）

Description 　　有n个木块排成一行，从左到右依次编号为1~n。你有k种颜色的油漆，其中第i种颜色的油漆足够涂ci个木块。所有油漆刚好足够涂满所有木块，即c1+c2+…+ck=n。相邻两个木块涂相同色显得很难看，所以你希望统计任意两个相邻木块颜色不同的着色方案。 Input 　　第一行为一个正整数k，第二行包含k个整数c1, c2, … , ck。 Output 　　输出一个整数

流通分量的_边框着色

文章目录 1、描述2、关键字3、思路4、notes5、复杂度6、code 1、描述给你一个大小为 m x n 的整数矩阵 grid ，表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。当两个网格块的颜色相同，而且在四个方向中任意一个方向上相邻时，它们属于同一连通分量。连通分量的边界是指连通分量中的所有与不在分

习题 8-9 K度图的着色（K-Graph Oddity, ACM/ICPC NEERC 2010, UVa1613）

原题链接：https://vjudge.net/problem/UVA-1613 分类：贪心法备注：简单思维题 #include<bits/stdc++.h>using namespace std;const int maxn=1e4+5;vector<int>e[maxn];int n,m,k,color[maxn];bool check(int x,int c){for(int

(装)发布Live Writer代码着色插件CNBlogs.CodeHighlighter

在解决了使用Windows Live Writer发博所遇到的“建分类、加标签、写摘要”与“设置EntryName”的四个问题之后，我们趁热打铁，解决了第五个问题 —— 代码着色的问题。代码着色以Live Writer插件的方式实现，采用了“云中着色”技术（呵呵，跟随当前云计算的潮流。实际只是将代码提交至服务器端处理）。该代码着色的特点是所见即所得，着色效果与博客后台编辑器中的一样。插

Java着色问题(含面试大厂题和源码)

图的着色问题是一个经典的图论问题，其目标是将图的顶点按照某种规则进行着色，使得相邻的顶点具有不同的颜色。图的着色问题可以应用于多种实际场景，如课程安排、频谱分配、地图着色等。以下是图的着色问题的一些关键知识点：基本概念顶点着色：给图的每个顶点分配一种颜色。合法着色：如果图中任意两个相邻的顶点都分配了不同的颜色，则称这种着色为合法的。色数：图的色数（chromatic number）是指对图

Games101-着色（着色频率、图形管线、纹理映射）

着色频率从边界可以看出三个球，拥有完全相同的几何形状。但是着色之后结果各不相同着色频率：着色要应用在哪些点上。第一个球，把着色应用在一个面上。一个平面只做一次shading。第二个球，每一个平面有4个顶点，每个顶点都算出对应的法线，进行shading。每3个顶点，可以围成一个三角形，三角形内部的颜色通过插值的方法计算第三个球，着色应用在每一个像素上。求出每一个三角形的法线，将法线进行

LeetCode 第 148 场周赛【递减元素使数组呈锯齿状】【二叉树着色游戏】

5147. 递减元素使数组呈锯齿状给你一个整数数组 nums，每次操作会从中选择一个元素并将该元素的值减少 1。如果符合下列情况之一，则数组 A 就是锯齿数组：每个偶数索引对应的元素都大于相邻的元素，即 A[0] > A[1] < A[2] > A[3] < A[4] > …或者，每个奇数索引对应的元素都大于相邻的元素，即 A[0] < A[1] > A[2] < A[3] >

C#，图论与图算法，图着色问题（Graph Coloring）的威尔士-鲍威尔（Welch Powell Algorithm）算法与源代码

Welsh, D.J.A. and Powell, M.B. (1967) An Upper Bound for the Chromatic Number of a Graph and Its Application to Timetabling Problems. 《The Computer Journal》, 10, 85-86. 《The Computer Journal》

【ASE入门学习】ASE入门系列九——软粒子与顶点着色

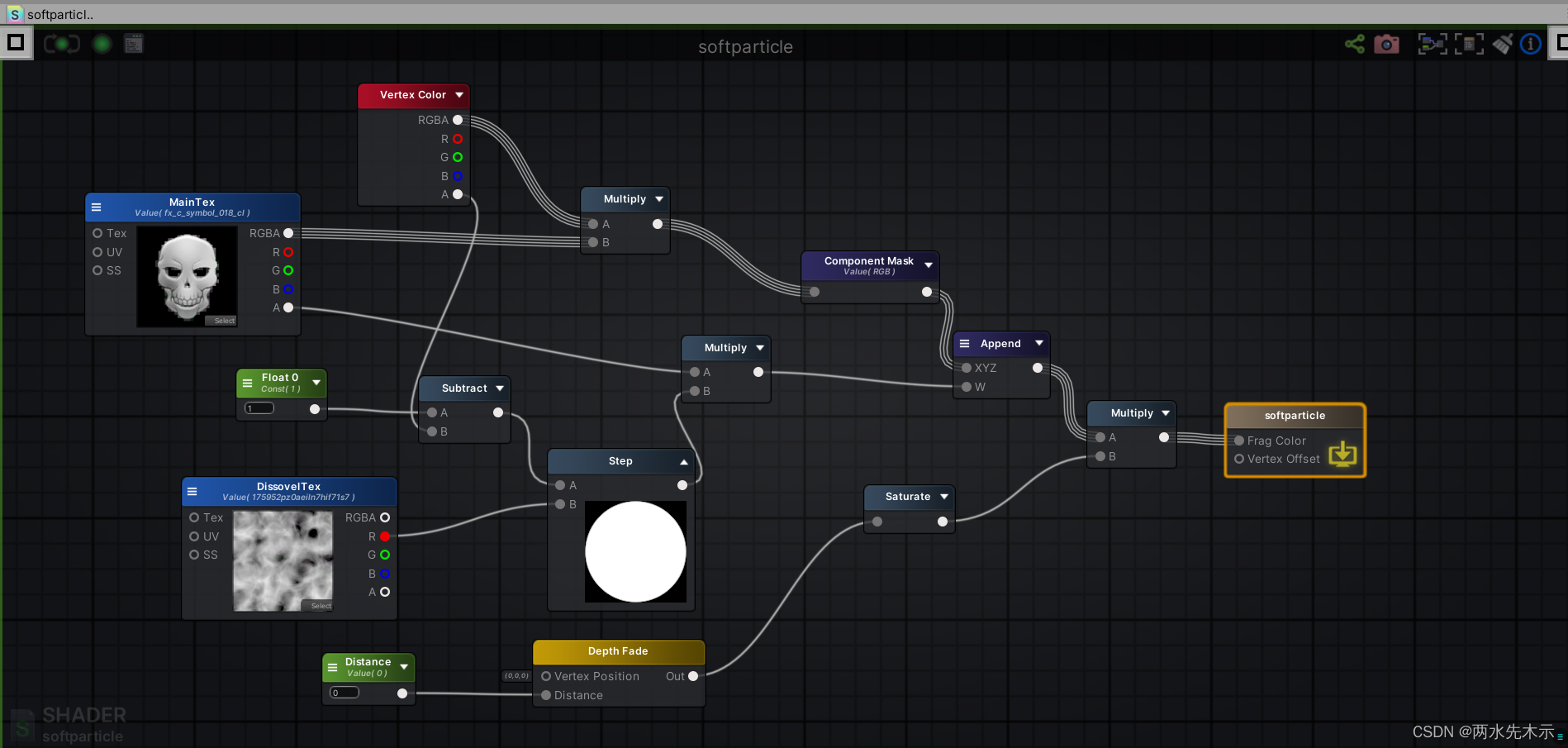
涵盖知识点：Depth Fade（软粒子）、粒子顶点着色、粒子消融、扩展——软粒子消融、深度图、深度写入、透明通道渲染顺序开启深度写入以及无软粒子（深度渐变）效果如上图，自身遮挡自身情况是开启深度写入导致，粒子与其他物体（地面）造成的切割感是没有实现深度渐变（非软粒子）表现。关闭深度写入后，自身粒子贴图不会遮挡其他自身粒子贴图了。假设我们在制作了一个深度写入的粒子（红色骷髅头

Cg Programming/Unity/Toon Shading卡通着色

本教程涵盖了卡通着色（也叫做卡通渲染）作为非真实感渲染技术的一个实例。奶牛图标。本节中的所有图片都由Mariana Ruiz提供。这是几个关于光照教程中的其中之一，这个光照超出了Phong反射模型的范围。但是，它是基于用章节“光滑镜面高光”中描述的Phong反射模型实现的逐像素光照。如果你还没有阅读过那章，建议你最好先读一下它。非真实感渲染是计算机图形学中的一个非常宽泛的术语，它涵盖了