【算法设计与分析】实验报告c++python实现(TSP问题、哈夫曼编码问题、顾客安排问题、最小生成树问题、图着色问题)

2024-05-03 15:36
文章标签 python 算法 分析 c++ 实现 设计 问题 最小 生成 编码 安排 着色 实验报告 顾客 哈夫曼 tsp

本文主要是介绍【算法设计与分析】实验报告c++python实现(TSP问题、哈夫曼编码问题、顾客安排问题、最小生成树问题、图着色问题)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、实验目的

1．加深学生对贪心算法设计方法的基本思想、基本步骤、基本方法的理解与掌握；
2．提高学生利用课堂所学知识解决实际问题的能力；
3．提高学生综合应用所学知识解决实际问题的能力。

二、实验任务

用贪心算法实现：
1、TSP问题
TSP问题（Travelling Salesman Problem）即旅行商问题，又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
2、哈夫曼编码问题
a.写一个程序，为给定的英文文本构造一套哈夫曼编码，并对该文本编码。
b.写一个程序，对一段用哈夫曼编码的英文文本进行解码。
c.做一个实验，测试对包含1000个词左右的一段英文文本进行哈夫曼编码时，典型的压缩率位于什么样的区间。
3、设有n个顾客同时等待一项服务，顾客i 需要的服务时间为ti ,i=1，2，3，…，n 。从时刻0开始计时，若在时刻t开始对顾客i服务，那么i的等待时间为t,应该怎么安排n个顾客的服务次序使得总的等待时间（每个顾客等待时间的总和）最少？
假设服务时间分别为{1，3，2，15，10，6，12}，用贪心算法给出这个问题的解。
4、最小生成树问题（Prim算法和Kruskal算法）
设G=(V，E)是一个无向连通网，生成树上各边的权值之和称为该生成树的代价，在G的所有生成树中，代价最小的生成树称为最小生成树（Minimal Spanning Trees）。
5、图着色问题
给定无向连通图G=(V, E)，求图G的最小色数k，使得用k种颜色对G中的顶点着色，可使任意两个相邻顶点着色不同。

三、实验设备及编程开发工具

笔记本，Windows10操作系统，Dev-C++，Pycharm

四、实验过程设计（算法设计过程）

（一）TSP问题

1、TSP问题

在TSP问题上，假设城市集合为B，我们每次只选择距离当前城市最近的城市移动。同时集合s记录已经遍历过得城市，下次从集合(B-s)中选择。

# 贪心法
import pandas as pd
import numpy as np
import math
import time
dataframe = pd.read_csv("./data/TSP100cities.tsp", sep=" ", header=None)
v = dataframe.iloc[:, 1:3]train_v = np.array(v)
train_d = train_v
dist = np.zeros((train_v.shape[0], train_d.shape[0]))# 计算距离矩阵
for i in range(train_v.shape[0]):for j in range(train_d.shape[0]):dist[i, j] = math.sqrt(np.sum((train_v[i, :] - train_d[j, :]) ** 2))
"""
s:已经遍历过的城市
dist：城市间距离矩阵
sumpath:目前的最小路径总长度
Dtemp：当前最小距离
flag：访问标记
"""
i = 1
n = train_v.shape[0]
j = 0
sumpath = 0
s = []
s.append(0)
start = time.clock()
while True:k = 1Detemp = 10000000while True:l = 0flag = 0if k in s:flag = 1if (flag == 0) and (dist[k][s[i - 1]] < Detemp):j = k;Detemp = dist[k][s[i - 1]];k += 1if k >= n:break;s.append(j)i += 1;sumpath += Detempif i >= n:break;
sumpath += dist[0][j]
end = time.clock()
print("结果：")
print(sumpath)
for m in range(n):print("%s-> " % (s[m]), end='')
print()
print("程序的运行时间是：%s" % (end - start))

（二）哈夫曼编码问题

(1)问题分析：
哈夫曼提出构造最优前缀码的贪心算法，由此产生的编码方案称为哈夫曼编码。其构造步骤如下：
(1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
(2)算法以|C|个叶结点开始，执行|C|－1次的“合并”运算后产生最终所要求的树T。
(3)假设编码字符集中每一字符c的频率是f©。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。

(2)算法实现：

import requests
# 实现节点类
class Node:def __init__(self, freq):self.left = Noneself.right = Noneself.father = Noneself.freq = freqdef is_left(self):return self.father.left == self# 为每一个节点赋权值
def create_nodes(frequencies):return [Node(freq) for freq in frequencies]# 创建哈夫曼树
def createHuffmanTree(nodes):queue = nodes[:]while len(queue) > 1:queue.sort(key=lambda item: item.freq)  # 将字符出现的频率视为权值，按权值排序。sort()默认升序排列node_left = queue.pop(0)  # 将弹出的第一个元素（最小）赋给左边节点node_right = queue.pop(0)node_father = Node(node_left.freq + node_right.freq)  # 将左右子树的权值相加赋给父节点# 构建节点之间的关系node_father.left = node_leftnode_father.right = node_rightnode_left.father = node_fathernode_right.father = node_fatherqueue.append(node_father)  # 将父节点插入到队列中queue[0].father = None  # 第一个节点没有父节点# print(type(queue[0]))  queue[0] 中保存的是什么数据return queue[0]# 遍历叶节点
def huffman_encoding(nodes, root):codes = [''] * len(nodes)for i in range(len(nodes)):node_tmp = nodes[i]while node_tmp != root:if node_tmp.is_left():codes[i] = '0' + codes[i]else:codes[i] = '1' + codes[i]node_tmp = node_tmp.fatherreturn codes# 获取字符出现的频数
def count_frequency(input_string):# 用于存放字符char_store = []# 用于存放频数freq_store = []# 解析字符串for index in range(len(input_string)):if char_store.count(input_string[index]) > 0:temp = int(freq_store[char_store.index(input_string[index])])temp = temp + 1freq_store[char_store.index(input_string[index])] = tempelse:char_store.append(input_string[index])freq_store.append(1)# 返回字符列表和频数列表return char_store, freq_store# 获取字符、频数的列表
def get_char_frequency(char_store=[], freq_store=[]):# 用于存放char_frequencychar_frequency = []for item in zip(char_store, freq_store):temp = (item[0], item[1])char_frequency.append(temp)return char_frequency# 解压缩huffman文件
def decode_huffman(input_string,  char_store, freq_store):encode = ''decode = ''for index in range(len(input_string)):encode = encode + input_string[index]for item in zip(char_store, freq_store):if encode == item[1]:decode = decode + item[0]encode = ''return decodeinput_string = input()
a, b = count_frequency(input_string)
char_freqs = get_char_frequency(a, b)
nodes = create_nodes([item[1] for item in char_freqs])
root = createHuffmanTree(nodes)
codes = huffman_encoding(nodes, root)
for item in zip(char_freqs, codes):print('Character:%s freq:%-2d   encoding: %s' % (item[0][0], item[0][1], item[1]))

（三）顾客等待问题

(1) 问题分析：
服务时间最小的顾客先服务，第一位顾客服务时，每一位顾客都等待A[0]个时间；第二个时，有n-1位顾客等待；以此类推，第i个顾客服务时，有n- i个顾客在等待中，由此得出公式 总的等待时间 time += （n - i） * A [ i ] ，最小平均等待时间为 time / n。

(2) 算法实现：

#include <stdio.h>
#include <string.h>
#define SIZE 10
int A[SIZE];
void sort(int A[],int n);
double greedy(int A[],int n);
void swap(int * a,int * b);int  main()
{int n,i;// n个顾客printf("请输入顾客数:\n");scanf("%d",&n);printf("请输入每个顾客的服务时间:\n");for(i = 1;i<=n;i++){printf("No.%d\n",i);scanf("%d",&A[i-1]);}sort(A,n);printf("最小平均等待时间:%.2f",greedy(A,n));return 0;
}double greedy(int A[],int n)
{int i,time = 0;double t = 0;//最小平均等待时间for(i = 0;i < n;i++){time = time +(n-i)*A[i];}t = time/n;return t;
}
void sort(int A[],int n)
{int i,j;for(i = 0;i < n;i++){for(j = i+1;j < n;j++){if(A[i] > A[j])swap(&A[i],&A[j]);}}
}
void swap(int *a,int *b)
{int temp;temp = *a;*a = *b;*b = temp;
}

（四）最小生成树问题

(1) Prim算法
任选一个顶点，并以此建立起生成树，每一步的贪心选择是简单地把不在生成树中的最近顶点添加到生成树中。设最小生成树T=(U,TE)，初始化时U={u0}（u0为任意顶点），TE={ }。Prim算法的关键是如何找到连接 U 和 V-U 的最短边来扩充生成树T。
对于每一个不在当前生成树中的顶点v∈ V-U，必须知道它连接生成树中每一个顶点u∈U的边信息，从中选择最短边。
所以，对当前不在生成树中的顶点v∈ V-U，需要保存两个信息：lowcost[v]表示顶点v到生成树中所有顶点的最短边；adjvex[v]表示该最短边在生成树中的顶点。

(2) Kruskal算法
设G=(V,E)是一个无向连通网，令T=(U,TE)是G的最小生成树。最短边策略从TE={ }开始，每一次贪心选择都是在边集E中选择最短边(u,v)，如果边(u,v)加入集合TE中不产生回路，则将边(u,v)加入边集TE中，并将它在集合E中删去。

class Graph(object):def __init__(self, maps):self.maps = mapsself.nodenum = self.get_nodenum()self.edgenum = self.get_edgenum()def get_nodenum(self):return len(self.maps)def get_edgenum(self):count = 0for i in range(self.nodenum):for j in range(i):if self.maps[i][j] > 0 and self.maps[i][j] < 9999:count += 1return countdef kruskal(self):res = []if self.nodenum <= 0 or self.edgenum < self.nodenum - 1:return resedge_list = []for i in range(self.nodenum):for j in range(i, self.nodenum):if self.maps[i][j] < 9999:edge_list.append([i, j, self.maps[i][j]])  # 按[begin, end, weight]形式加入edge_list.sort(key=lambda a: a[2])  # 已经排好序的边集合group = [[i] for i in range(self.nodenum)]for edge in edge_list:for i in range(len(group)):if edge[0] in group[i]:m = iif edge[1] in group[i]:n = iif m != n:res.append(edge)group[m] = group[m] + group[n]group[n] = []return resdef prim(self):res = []if self.nodenum <= 0 or self.edgenum < self.nodenum - 1:return resres = []seleted_node = [0]candidate_node = [i for i in range(1, self.nodenum)]while len(candidate_node) > 0:begin, end, minweight = 0, 0, 9999for i in seleted_node:for j in candidate_node:if self.maps[i][j] < minweight:minweight = self.maps[i][j]begin = iend = jres.append([begin, end, minweight])seleted_node.append(end)candidate_node.remove(end)return resmax_value = 9999
row0 = [0, 7, max_value, max_value, max_value, 5]
row1 = [7, 0, 9, max_value, 3, max_value]
row2 = [max_value, 9, 0, 6, max_value, max_value]
row3 = [max_value, max_value, 6, 0, 8, 10]
row4 = [max_value, 3, max_value, 8, 0, 4]
row5 = [5, max_value, max_value, 10, 4, 0]
maps = [row0, row1, row2, row3, row4, row5]
graph = Graph(maps)
print('邻接矩阵为\n%s' % graph.maps)
print('节点数据为%d，边数为%d\n' % (graph.nodenum, graph.edgenum))
print('------最小生成树kruskal算法------')
print(graph.kruskal())
print('------最小生成树prim算法')
print(graph.prim())

（五）图着色问题

(1) 问题分析：
图的m色优化问题:给定无向连通图G,为图G的各顶点着色, 使图中任2邻接点着不同颜色,问最少需要几种颜色。所需的最少颜色的数目m称为该图的色数。
若图G是可平面图,则它的色数不超过4色(4色定理).
4色定理的应用:在一个平面或球面上的任何地图能够只用4种
颜色来着色使得相邻的国家在地图上着有不同颜色。
(2) 算法实现：

#include<stdio.h>int color[100];
//int c[100][100];
bool ok(int k ,int c[][100])//判断顶点k的着色是否发生冲突
{int i,j;for(i=1;i<k;i++)if(c[k][i]==1&&color[i]==color[k])return false;return true;
}void graphcolor(int n,int m,int c[][100])
{int i,k;for(i=1;i<=n;i++)color[i]=0;//初始化k=1;while(k>=1){color[k]=color[k]+1;while(color[k]<=m)if (ok(k,c)) break;else color[k]=color[k]+1;//搜索下一个颜色if(color[k]<=m&&k==n)//求解完毕，输出解{for(i=1;i<=n;i++)printf("%d ",color[i]);printf("\n");//return;//return表示之求解其中一种解}else if(color[k]<=m&&k<n)k=k+1;    //处理下一个顶点else{color[k]=0;k=k-1;//回溯}}
}
void main()
{int i,j,n,m;int c[100][100];//存储n个顶点的无向图的数组printf("输入顶点数n和着色数m:\n");scanf("%d %d",&n,&m);printf("输入无向图的邻接矩阵:\n");for(i=1;i<=n;i++)for(j=1;j<=n;j++)scanf("%d",&c[i][j]);printf("着色所有可能的解:\n");graphcolor(n,m,c);
}

五、实验结果及算法复杂度分析
（一）TSP问题
img
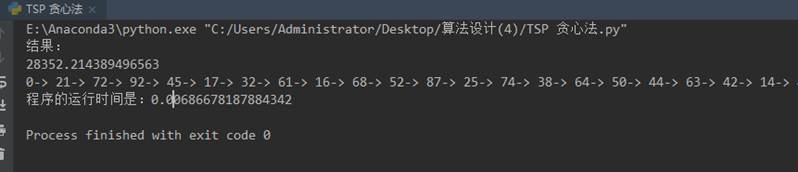
（二)哈夫曼编码问题
img
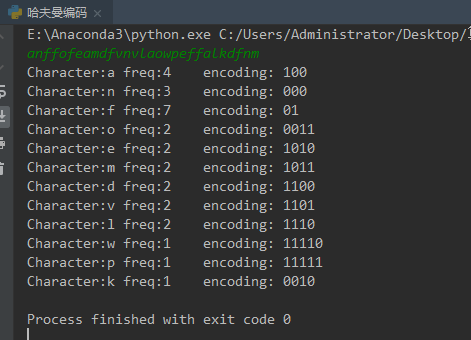
（三)动态服务问题

img
（四）最小生成树问题
img

(1)Prim算法
设连通网中有 n 个顶点，则第一个进行初始化的循环语句需要执行 n-1 次，第二个循环共执行 n-1 次，内嵌两个循环，其一是在长度为 n 的数组中求最小值，需要执行 n-1 次，其二是调整辅助数组，需要执行 n-1 次，所以，Prim 算法的时间复杂度为O(n2)。
(2) Kruskal算法
为了提高每次贪心选择时查找最短边的效率，可以先将图G中的边按代价从小到达排序，则这个操作的时间复杂度为O(elog2e)，其中e为无向连通网中边的个数。对于两个顶点是否属于同一个连通分量，可以用并查集的操作将其时间性能提高到O(n)，所以Kruskal算法的时间性能是O(elog2e)。

（五）图着色问题
img

实验小结（包括问题和解决方法、心得体会等）

通过本次实验，利用C/python语言编程实现解决了TSP问题，哈夫曼编码问题，顾客等待问题，最小生成树问题。对贪心算法有了更进一步的认识，对算法设计这门课程有了更多的认识。

本次实验增加了动手编码能力，对算法设计有了更进一步的认识，但是技术上的缺陷，编码能力上存在的短板，在今后的实验中还需要加大练习力度。

这篇关于【算法设计与分析】实验报告c++python实现(TSP问题、哈夫曼编码问题、顾客安排问题、最小生成树问题、图着色问题)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/957068。

相关文章

不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
python: 多模块(.py)中全局变量的导入

python: 多模块(.py)中全局变量的导入

文章目录 global关键字可变类型和不可变类型数据的内存地址单模块(单个py文件)的全局变量示例总结 多模块(多个py文件)的全局变量from x import x导入全局变量示例 import x导入全局变量示例 总结 global关键字 global 的作用范围是模块(.py)级别： 当你在一个模块（文件）中使用 global 声明变量时，这个变量只在该模块的全局命名空
阅读更多...
好题——hdu2522（小数问题：求1/n的第一个循环节）

好题——hdu2522（小数问题：求1/n的第一个循环节）

好喜欢这题，第一次做小数问题，一开始真心没思路，然后参考了网上的一些资料。 知识点***********************************无限不循环小数即无理数，不能写作两整数之比*****************************（一开始没想到，小学没学好） 此题1/n肯定是一个有限循环小数，了解这些后就能做此题了。 按照除法的机制，用一个函数表示出来就可以了，代码如下
阅读更多...
hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

利用康拓展开将一个排列映射成一个自然数，然后就变成了普通的广搜题。 #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#inclu
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
【C++ Primer Plus习题】13.4

【C++ Primer Plus习题】13.4

大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream>#include "port.h"int main() {Port p1;Port p2("Abc", "Bcc", 30);std::cout <<
阅读更多...
AI一键生成 PPT

AI一键生成 PPT

AI一键生成 PPT 操作步骤 作为一名打工人，是不是经常需要制作各种PPT来分享我的生活和想法。但是，你们知道，有时候灵感来了，时间却不够用了！😩直到我发现了Kimi AI——一个能够自动生成PPT的神奇助手！🌟 什么是Kimi？ 一款月之暗面科技有限公司开发的AI办公工具，帮助用户快速生成高质量的演示文稿。 无论你是职场人士、学生还是教师，Kimi都能够为你的办公文
阅读更多...
性能分析之MySQL索引实战案例

性能分析之MySQL索引实战案例

文章目录 一、前言二、准备三、MySQL索引优化四、MySQL 索引知识回顾五、总结 一、前言 在上一讲性能工具之 JProfiler 简单登录案例分析实战中已经发现SQL没有建立索引问题，本文将一起从代码层去分析为什么没有建立索引？ 开源ERP项目地址：https://gitee.com/jishenghua/JSH_ERP 二、准备 打开IDEA找到登录请求资源路径位置
阅读更多...
csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

这是一道扩展欧几里得算法的简单应用题，这题是在湖南多校训练赛中队友ac的一道题，在比赛之后请教了队友，然后自己把它a掉 这也是自己独自做扩展欧几里得算法的题目 题意：把题意转变下就变成了：求d1*x - d2*y = f2 - f1的解,很明显用exgcd来解 下面介绍一下exgcd的一些知识点：求ax + by = c的解 一、首先求ax + by = gcd(a,b)的解 这个
阅读更多...
C++包装器

C++包装器

包装器 在 C++ 中，“包装器”通常指的是一种设计模式或编程技巧，用于封装其他代码或对象，使其更易于使用、管理或扩展。包装器的概念在编程中非常普遍，可以用于函数、类、库等多个方面。下面是几个常见的 “包装器” 类型： 1. 函数包装器 函数包装器用于封装一个或多个函数，使其接口更统一或更便于调用。例如，std::function 是一个通用的函数包装器，它可以存储任意可调用对象（函数、函数
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2