本文主要是介绍【图论及其运用 — 电子科技大学】(七)第七章 图的着色,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、图的边着色
(一)、相关概念

定义1 给定图 G = ( V , E ) G=(V,E) G=(V,E),称映射 π : E → { 1 , 2 , 3 , . . . , k } \pi : E \to \{1, 2, 3, ..., k\} π:E→{1,2,3,...,k} 为 G G G 的一个 k k k 边着色,简称边着色,称 { 1 , 2 , 3 , . . . , k } \{1, 2, 3, ..., k\} {1,2,3,...,k} 为色集。若 π \pi π 为 G G G 的边着色且 ∀ e ′ , e ′ ′ ∈ E \forall e{'}, e{''} \in E ∀e′,e′′∈E,当
e ′ 与 e ′ ′ e{'} 与 e{''} e′与e′′ 相邻时, π ( e ′ ) ≠ π ( e ′ ′ ) \pi(e') ≠ \pi(e'') π(e′)=π(e′′),则称该着色是正常的。图 G G G 的正常 k k k 边着色的最小值 k k k 称为 G G G 的边色数。( π ( e ) \pi(e) π(e) 为图 G G G 的边着色, e e e 为 G G G 的边)
即 G G G 是图,对 G G G的边进行染色,若相邻边染不同颜色,则称对 G G G进行正常边着色;
如果能用 k k k种颜色对图 G G G进行正常边着色,称 G G G是 k k k边可着色的。

定义2 设 G G G是图,对 G G G进行正常边着色需要的最少颜色数,称为 G G G的边色数,记为: χ ′ ( G ) \chi^{\prime}(G) χ′(G) ( χ \chi χ 读为 kappa)
注: 对图的正常边着色,实际上是对 G G G的边集合的一种划分,使得每个划分块是 G G G的一个边独立集(无环时是匹配); 图的边色数对应的是图的最小独立集划分数。
因此,图的边着色,本质上是对应实际问题中的“划分”问题或“分类”问题。
在对 G G G正常边着色时,着相同颜色的边集称为该正常着色的一个色组。
(二)、几类特殊图的边色数
1、偶图的边色数
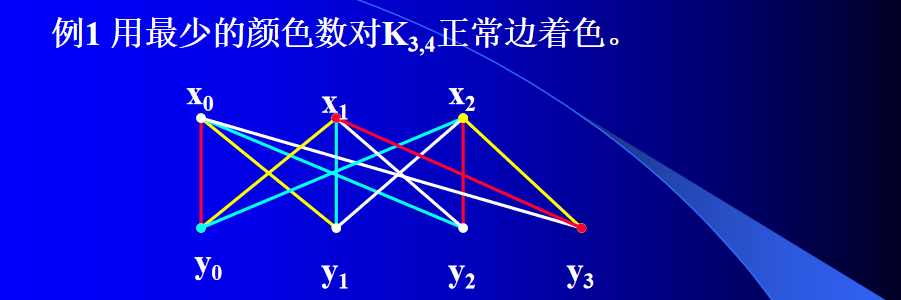
定理 1 χ ′ ( K m , n ) = Δ \chi^{\prime}(K_{m,n})=\Delta χ′(Km,n)=Δ (完全偶图的边色数 = 最大度)
完全偶图的最大度为,当 m > n,最大度为 m, 当 n > m,最大度为 n
且任何正常边着色中和任何一个顶点关联得各边必须着不同色,因此 χ ′ ≥ Δ \chi^{\prime} ≥ \Delta χ′≥Δ

使用上面定理,使用最大度的颜色:4 进行边着色
定义3 设 π \pi π是 G G G的一种正常边着色,若点 u u u关联的边的着色没有用到色 i i i,则称点 u u u缺 i i i色。
定理2 (哥尼,1916) 若 G G G是偶图,则 χ ′ ( G ) = Δ \chi^{\prime}(G)=\Delta χ′(G)=Δ

2、一般简单图的边色数
引理: 设 G G G是简单图, x x x与 y 1 y_1 y1是 G G G中不相邻的两个顶点, π \pi π是 G G G的一个正常 k k k边着色。若对该着色 π , x , y 1 \pi, x,y_1 π,x,y1以及与 x x x 相邻点均至少缺少一种颜色,则 G + x y 1 G+xy_1 G+xy1 是 k k k边可着色的。

定理3 (维津定理,1964) 若 G G G是单图,则: χ ′ ( G ) = Δ 或 χ ′ ( G ) = Δ + 1 \chi^{\prime}(G)=\Delta\text{或 }\chi^{\prime}(G)=\Delta+1 χ′(G)=Δ或 χ′(G)=Δ+1
为什么这里会说 G 1 G_1 G1 的 Δ ( G ) + 1 \Delta(G) + 1 Δ(G)+1 正常边着色,会显然每个顶点都至少缺少一种颜色?
很显然, G 1 G_1 G1 的最大度为 Δ ( G ) \Delta(G) Δ(G),而为这个最大度进行边着色,最多只需用到 Δ ( G ) \Delta(G) Δ(G) 种颜色, Δ ( G ) + 1 \Delta(G) + 1 Δ(G)+1 正常边着色,肯定至少要剩一种颜色出来。

注: (1) 根据维津定理,单图可以按边色数分成两类图,一是色数等于 Δ ( G ) Δ(G) Δ(G)的单图,二是色数等于 Δ ( G ) + 1 Δ(G)+1 Δ(G)+1的单图。
3、三类特殊简单图的边色数
定理4 设 G G G是单图且 Δ ( G ) > 0 Δ(G)>0 Δ(G)>0。若 G G G中只有一个最大度点或恰有两个相邻的最大度点,则: χ ′ ( G ) = Δ ( G ) \chi^{\prime}(G)=\Delta(G) χ′(G)=Δ(G)


定理5 设 G G G是单图。若点数 n = 2 k + 1 n=2k+1 n=2k+1 且边数 m > k Δ m>kΔ m>kΔ, 则: χ ′ ( G ) = Δ ( G ) + 1 \chi^{\prime}(G)=\Delta(G)+1 χ′(G)=Δ(G)+1
为什么着同色的边最多 n − 1 2 \frac{n - 1}{2} 2n−1 ? 是因为假设这 n n n 个点组成一条路,某个颜色交替的在这条路上进行着色,也只有 k k k 条边着这个色。
为什么边数最多 k Δ k \Delta kΔ ,是因为着某个颜色最多只能着 k k k 条,如果最小着色集 χ ′ = Δ \chi' = \Delta χ′=Δ,那么能着的色做多也就是 k Δ k \Delta kΔ



顶点数 n = 2 ∗ 2 + 1 = 5 n = 2 * 2 + 1 = 5 n=2∗2+1=5,且 m = 9 > 2 ∗ 4 m = 9 > 2 * 4 m=9>2∗4,因此 χ ′ = Δ + 1 \chi' = \Delta + 1 χ′=Δ+1
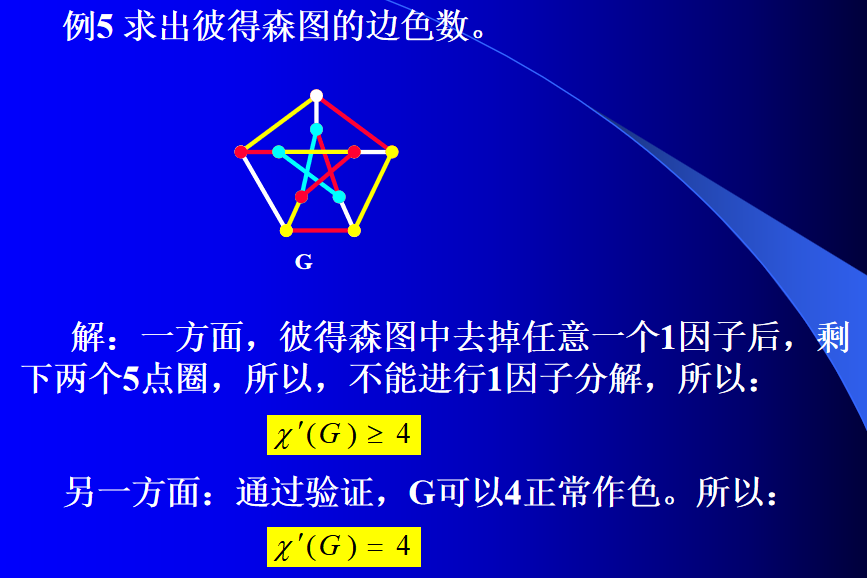
定理6 设 G G G是奇数阶 Δ Δ Δ正则单图, 若 Δ > 0 Δ>0 Δ>0, 则: χ ′ ( G ) = Δ ( G ) + 1 \chi^{\prime}(G)=\Delta(G)+1 χ′(G)=Δ(G)+1
Δ \Delta Δ 正则单图,每个顶点度为 Δ \Delta Δ,则边数为 n Δ 2 \frac{n \Delta}{2} 2nΔ,

C n C_n Cn 的每个点度为 2,满足奇数阶正则单图

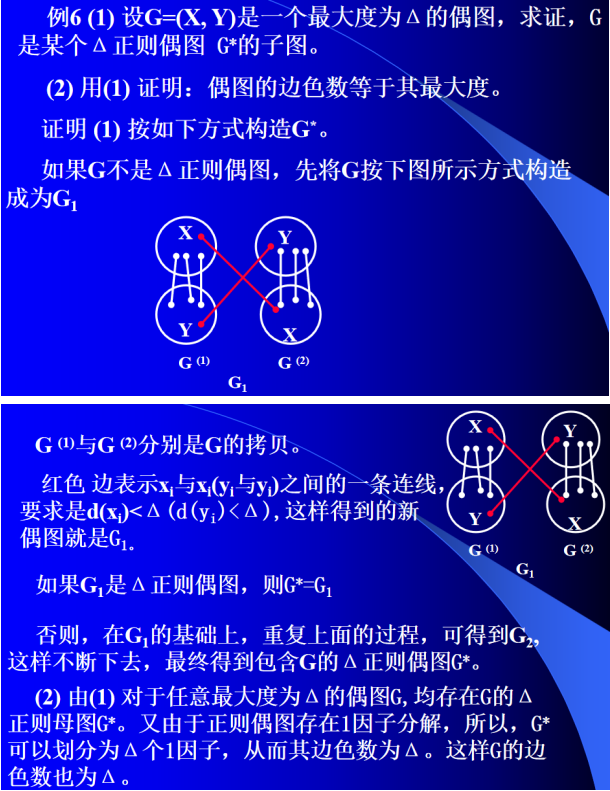

(三)、边着色的应用
边着色对应的实际问题就是图的匹配分解问题。边色数对应的是最小匹配分解问题。所以,生活中的许多问题都可模型为边着色问题来解决。
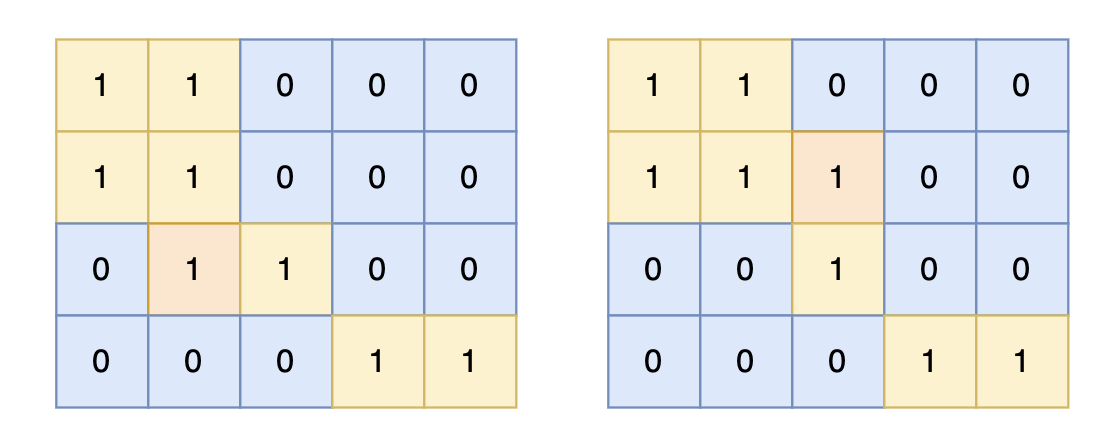
例 1 中(1)问每一行的和就代表 x i x_i xi 的度数,每一列之和就代表 y i y_i yi 的度数,边着色的最大度即找最大的行或列的和
(2)每天 8 节课,一周就是 40 节课,总课时是 240 ,教室就是 240 / 40


P187—190 习题7 :1----6
二、图的顶点着色
(一)、相关概念
跟图的边着色问题一样,生活中的很多问题,也可以模型为所谓的图的顶点着色问题来处理。例如课程安排问题。
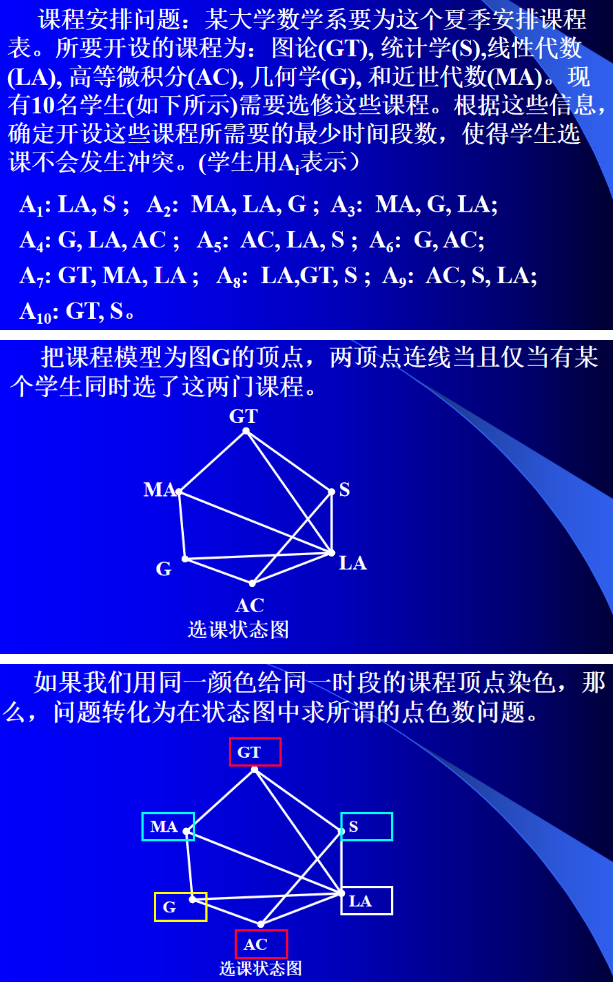
定义1 设 G G G是一个图,对 G G G的每个顶点着色,使得相邻顶点着不同颜色,称为对 G G G的正常顶点着色;
定义1 给定图 G = ( V , E ) G=(V,E) G=(V,E),称映射 π : V → { 1 , 2 , 3 , . . . , k } \pi : V \to \{1, 2, 3, ..., k\} π:V→{1,2,3,...,k} 为 G G G 的一个 k k k 点着色,简称着色,称 { 1 , 2 , 3 , . . . , k } \{1, 2, 3, ..., k\} {1,2,3,...,k} 为色集。若 π \pi π 为 G G G 的点着色且 ∀ u , v ∈ E \forall u, v \in E ∀u,v∈E,当
u 与 v u 与 v u与v 相邻时, π ( u ) ≠ π ( v ) \pi(u) ≠ \pi(v) π(u)=π(v),则称该着色是正常的。图 G G G 的正常 k k k 着色的最小值 k k k 称为 G G G 的色数。( π ( u ) \pi(u) π(u) 为图 G G G 的点着色, u u u 为 G G G 的顶点)
如果用 k k k种颜色可以对 G G G进行正常顶点着色,称 G G G可 k k k正常顶点着色;
对图 G G G正常顶点着色需要的最少颜色数,称为图 G G G的点色数。图 G G G的点色数用 χ ( G ) \chi\left(G\right) χ(G) 表示。
注: 对图的正常顶点着色,带来的是图的顶点集合的一种划分方式。所以,对应的实际问题也是分类问题。属于同一种颜色的顶点集合称为一个 色组,它们彼此不相邻接,所以又称为点独立集。用点色数种颜色对图 G G G正常着色,称为对图 G G G的最优点着色。(一个色组就是一个点独立集)
定义2 色数为 k k k的图称为 k k k色图。
(二)、图的点色数的几个结论(了解性学习)
定理1 对任意的图 G G G,有: χ ( G ) ≤ Δ ( G ) + 1 \left.\chi\left(G\right.\right)\leq\Delta\left(G\right.)+1 χ(G)≤Δ(G)+1
分析: 事实上,定理结论容易想到,因为任意一个顶点度数至多为 Δ Δ Δ,因此,正常着色过程中,其邻点最多用去 Δ Δ Δ种颜色,所以,至少还有一种色可供该点正常着色使用。

对于 G G G来说,可以给出其 Δ ( G ) + 1 Δ(G)+1 Δ(G)+1正常点着色算法。

其中的 C ( v i ) C(v_i) C(vi)

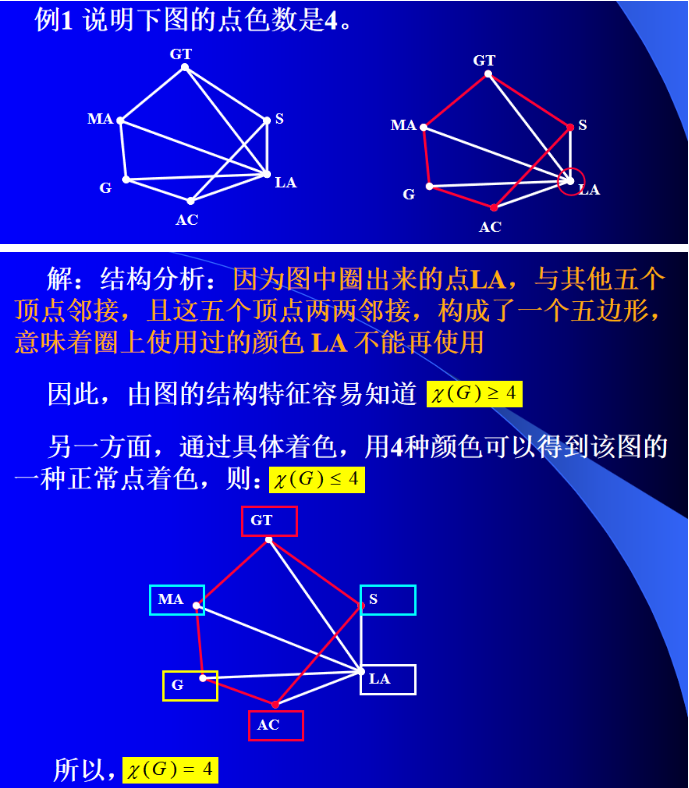
注: (1)不能通过上面算法求出色数,例如,根据上面算法,我们求出了一个4色方案,但G是3色图:
(2) Welsh—Powell稍微对上面算法做了一个修改,着色时按所谓最大度优先策略,即使用上面算法时,按顶点度数由大到小的次序着色。这样的着色方案起到了对上面算法的一个改进作用。
对于简单图 G G G来说,数学家布鲁克斯(Brooks)给出了一个对定理 1 1 1的色数改进界。这就是下面著名的布鲁克斯定理。
定理2(布鲁克斯,1941) 若 G G G是连通的单图,并且它既不是奇圈,又不是完全图,则: χ ( G ) ≤ Δ ( G ) \chi\left(G\right)\leq\Delta\left(G\right) χ(G)≤Δ(G)
对于简单图的点色数,还可以在定理2的基础上获得改进。
定义3 设 G G G是至少有一条边的简单图,定义:
Δ 2 ( G ) = max u ∈ V ( G ) max v ∈ N ( u ) d ( v ) ≤ d ( u ) d ( v ) \Delta_2(G)=\max_{u\in V(G)}\max_{\begin{array}{c}v\in N\left(u\right)\\d\left(v\right)\leq d\left(u\right)\end{array}}d\left(v\right) Δ2(G)=u∈V(G)maxv∈N(u)d(v)≤d(u)maxd(v)
如果令: V 2 ( G ) = { v ∣ v ∈ V ( G ) , N ( V ) 中 存在点 u , 满足 d ( u ) ≥ d ( V ) } V_2(G)=\begin{Bmatrix}v|v\in V(G),N(V)\text{中 存在点}u\text{, 满足}d(u)\geq d(V)\end{Bmatrix} V2(G)={v∣v∈V(G),N(V)中 存在点u, 满足d(u)≥d(V)}
那么,
Δ 2 ( G ) = max { d ( v ) ∣ v ∈ V 2 ( G ) } \Delta_2\left(G\right)=\max\left\{d\left(v\right)|v\in V_2(G)\right\} Δ2(G)=max{d(v)∣v∈V2(G)}

注: 由次大度的定义知: Δ 2 ( G ) ≦ Δ ( G ) Δ_2(G)≦Δ(G) Δ2(G)≦Δ(G)
定理3 设 G G G是非空简单图,则: χ ( G ) ≤ Δ 2 ( G ) + 1 \chi(G)\leq\Delta_2(G)+1 χ(G)≤Δ2(G)+1
注: 定理3是对定理2的一个改进!
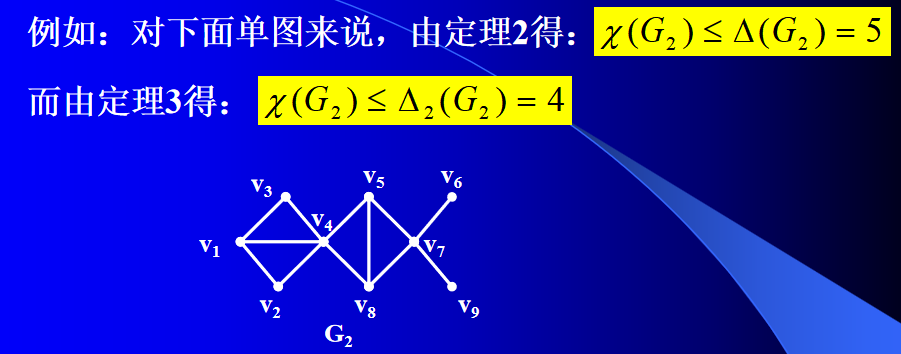
推论: 设 G G G是非空简单图,若 G G G中最大度点互不邻接,则有: χ ( G ) ≤ Δ ( G ) \chi(G)\leq\Delta(G) χ(G)≤Δ(G)
(三)、四色与五色定理
1、四色定理
2、五色定理
定理4 (希伍德) 每个平面图是 5 5 5可着色的。
根据平面图和其对偶图的关系,上面定理等价于每个平面图是 5 5 5可顶点正常着色的。

(四)、顶点着色的应用
图的正常顶点着色对应的实际问题是“划分”问题。

P187—190 习题7 :7----9
三、与色数有关的几类图和完美图(不管)
(一)、与色数有关的几类图
1、临界图
定义1 若对图 G G G的任意真子图 H H H,都有 χ ( H ) < χ ( G ) \chi(H)<\chi(G) χ(H)<χ(G),则称 G G G是临界图。点色数为 k k k的临界图称为 k k k临界图。

注: 临界图由狄拉克在1952年首先提出并研究。上面的4临界图是Grotzsch(格勒奇)在1958年提出的。
定理1 临界图有如下性质
(1) k k k色图均有 k k k临界子图;
(2) 每个临界图均为简单连通图;
(3) 若 G G G是 k k k临界图,则 δ ≥ k − 1 δ≥k-1 δ≥k−1。
证明: (1)是显然的。
(2) 因为删掉环或平行边中的一条边并不破坏原有的顶点正常着色,所以每个临界图是单图;又因为删掉色数较小的分支,剩下部分的图的色数和原图色数相等,所以,临界图必须是连通图。
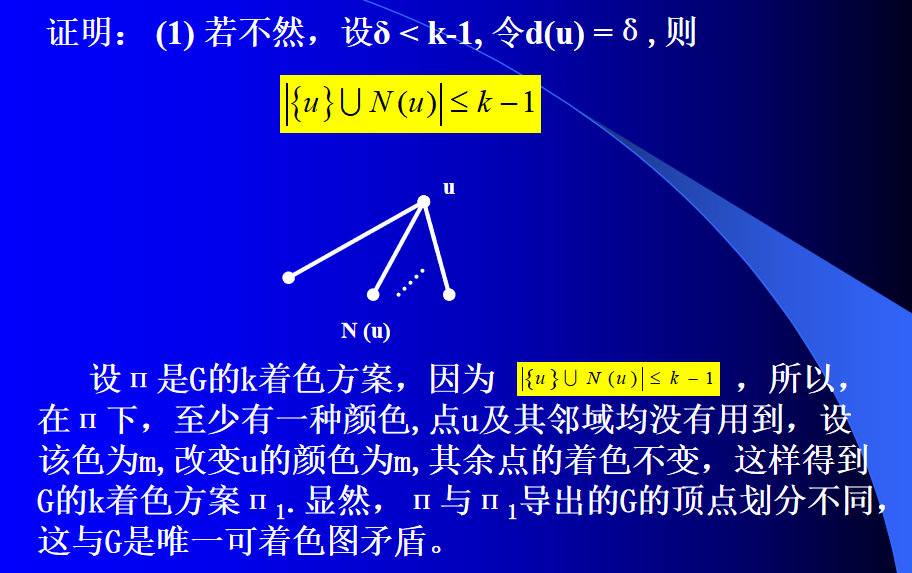
(3) 若不然, δ < k − 1 δ< k-1 δ<k−1。
设 d ( v ) = δ d(v)=δ d(v)=δ。因为 G G G是 k k k临界图,所以 G − v G-v G−v是 k − 1 k-1 k−1可正常顶点着色的。设 п п п是 G − v G-v G−v的 k − 1 k-1 k−1正常顶点着色方案,显然,它可以扩充为 G G G的 k − 1 k-1 k−1正常点着色方案。这与 G G G是 k k k临界图相矛盾。
推论: 每个 k k k色图至少有 k k k个度不小于 k − 1 k-1 k−1的顶点。





(2) 由例4中命题推布鲁克斯定理。

2、唯一可着色图
对图的顶点进行正常着色,实际上给出图的顶点集合的一种划分,不同的着色方案,给出的划分一般不同。但是,也存在一类特殊图,对于任意的最优着色方案,导出的顶点划分却是相同的。为此,我们给出如下定义。
定义2 设简单标定图 G G G的点色数是 k k k, 如果在任意的 k k k正常点着色方案下,导出的顶点集合划分唯一,称 G G G是唯一 k k k可着色图,简称唯一可着色图。
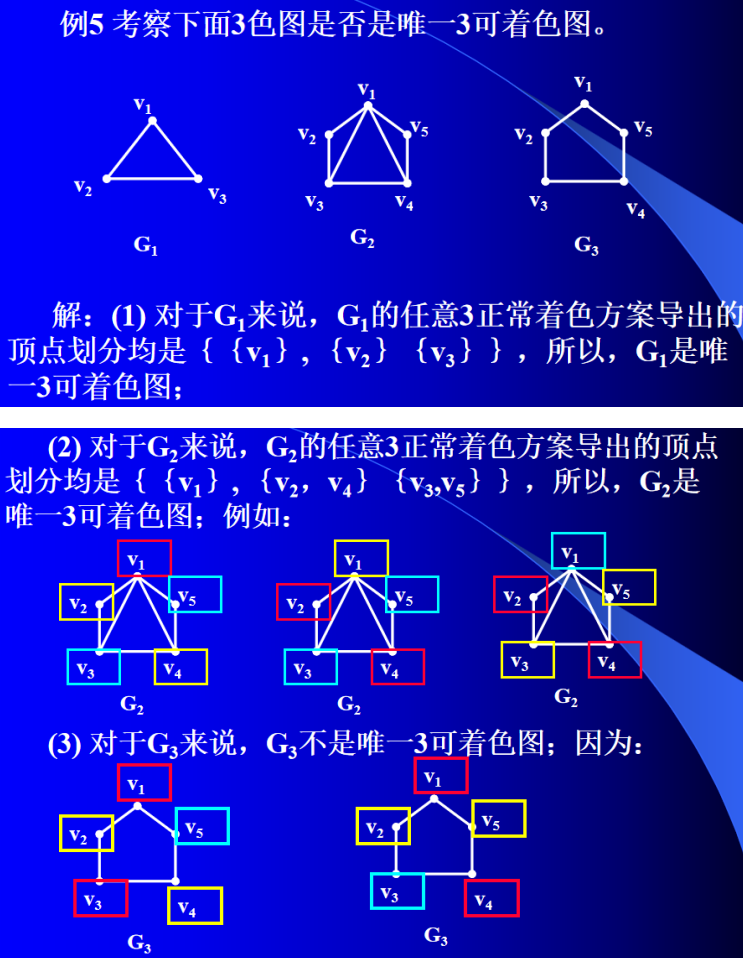
下面给出唯一可着色图的几个特征。
定理2(哈拉里,1968) 设 G G G是唯一 k k k可着色图, k ≥ 2 k≥2 k≥2, 则:
(1) δ ≥ k − 1 δ≥k-1 δ≥k−1;
(2) 在 G G G的任意一种 k k k着色中, G G G的任意两个色组的并的导出子图是连通的。

定理3 (夏特朗) 每个唯一 k ( k ≥ 2 ) k (k≥2) k(k≥2)可着色图是 ( k − 1 ) (k-1) (k−1)连通的。

推论: 设 G G G是唯一 n ( n ≥ 2 ) n(n≥2) n(n≥2)可着色图, п п п是任意一种 n n n着色方案,则由 п п п的任意 k k k个色组导出的子图是 ( k − 1 ) (k-1) (k−1)连通的。
证明: 显然,任意 k k k个色组导出子图是唯一 k k k可着色图,由定理3得到推论结论。
注: (1) 唯一1可着色图是零图;
(2) 唯一2可着色图是偶图;
除此之外,没有简单的结论!
定理4 每个唯一4可着色可平面图都是极大可平面图。

3、不含三角形的k色图
定义3 若图 G G G的点色数是 k k k,且 G G G中不含有三角形,称 G G G是一个不含三角形的 k k k色图。
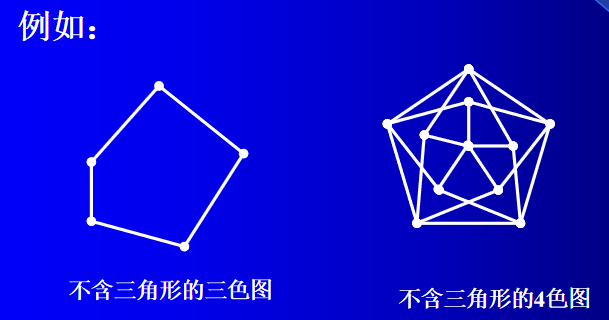
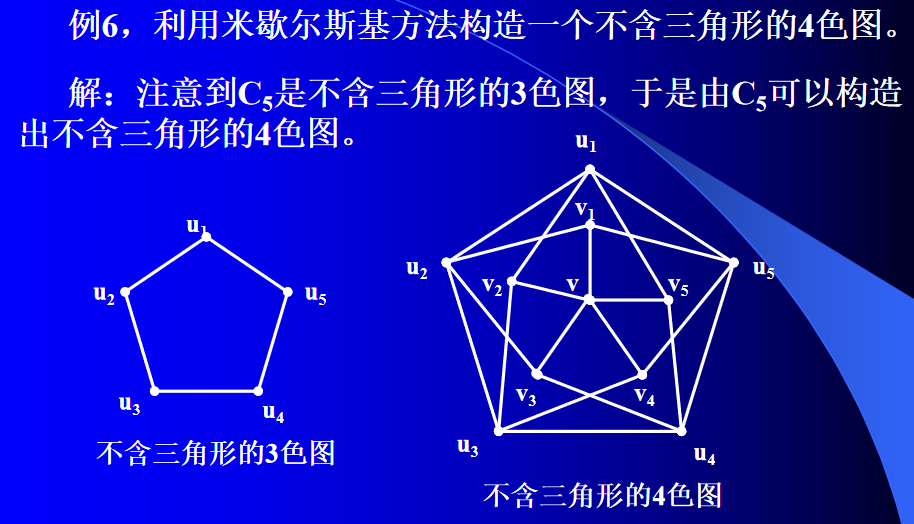
注: 利用米歇尔斯基方法构造一个不含三角形的k色图时,结果图与初始图有关。

定理5 (米歇尔斯基) 对于任意正整数 k k k, 存在不含三角形的 k k k色图。
定理6 (Erdos) 对于任意正整数 m m m和 n n n, 存在一个围长超过 m m m的 n n n色图。
(二)、完美图简介
1、相关概念
定义4 (1)单图 G G G的团:若单图 G G G的一个顶点子集 S S S在 G G G中的导出子图是完全图,则称 S S S是 G G G的一个团;
(2) 单图 G G G的团数:单图 G G G的最大团包含的顶点数称为 G G G的团数,记为 c l ( G ) c l (G) cl(G),即: c l ( G ) = max { ∥ S ∥ S 是 G 的团 } cl(G)=\max\left\{\left\|S\right\|S\text{是}G\text{的团}\right\} cl(G)=max{∥S∥S是G的团}
显然,图 G G G的点色数与团数的关系为:
χ ( G ) ≥ c l ( G ) \chi(G)\geq cl(G) χ(G)≥cl(G)
定义5 设 G G G是一个图。若对 G G G的每个点导出子图 H H H,均有 χ ( H ) = c l ( H ) \chi(H)=cl(H) χ(H)=cl(H) ,则称 G G G为完美图。
例如 K n K_n Kn, 偶图是完美图,而不含三角形但含奇圈的图不是完美图。
因为不含三角形的但含奇圈的图的团数为2,但色数为3,所以,它不能是完美图。
注:完美图问题是点着色的进一步讨论题材,属于比较高深和困难的问题。
定义6 设 G G G是一个图。由 G G G中若干互不邻接的顶点作成的子集称为 G G G的一个点独立集; G G G中含顶点数最多的点独立集称为 G G G的最大独立集,其包含的顶点数称为独立数。
图 G G G的点独立数记为 α ( G ) α(G) α(G)或 α α α。
注: 关于图的覆盖与图的点独立数之间的关系,加莱得到了一些很漂亮的结论。
2、关于独立数的完美图
定义7 设 S S S是图 G G G的顶点集合的一个划分。如果 S S S的每个子集在 G G G中的导出子图均是完全图,称 S S S是 G G G的一个完全分类。 G G G的最小完全分类所包含的元素个数称为 G G G的完全数,记为 θ ( G ) θ(G) θ(G),即:
θ ( G ) = min { ∣ S ∣ ∣ S 为G的完全分类 } \theta(G)=\min\left\{|S||S\text{为G的完全分类}\right\} θ(G)=min{∣S∣∣S为G的完全分类}
注: α ( G ) ≤ θ ( G ) \alpha(G)\leq\theta(G) α(G)≤θ(G)。这是因为独立集中任意一点应该属于 S S S中的某个顶点子集,同时, S S S中每个顶点子集最多包含独立集中的一个元素。
定义8 若对 G G G中每个点导出子图 H H H,都有 α ( G ) = θ ( G ) \alpha(G)=\theta(G) α(G)=θ(G), 称 G G G是关于点独立集的完美图。
定理7 (完美图定理) G G G是关于色数的完美图当且仅当 G G G是关于独立集的完美图。
定理8 G G G是完美图当且仅当其补图是完美图。
3、关于完美图的结构研究
在关于完美图结构的问题上,贝尔热提出了下面的强完美图猜想(SPGC猜想)
定理9 (强完美图定理) 图 G G G是完美的当且仅当 G G G和其补图均没有导出子图是长度至少为 5 5 5的奇圈。
注: 强完美图定理是一个还没有被证明的公开性问题,所以,现在还是一个吸引许多学者研究的问题。
P187—190 习题7 :22 ,23,24,26
四、着色的计数与色多项式
(一)、色多项式概念
所谓色计数,就是给定标定图 G G G和颜色数 k k k,求出正常顶点着色的方式数。方式数用 P k ( G ) P_k(G) Pk(G)表示。
可以证明: P k ( G ) P_k(G) Pk(G)是 k k k 的多项式,称为图 G G G 的色多项式。
由点色数 χ ( G ) \chi(G) χ(G) 和色多项式 P k ( G ) P_k(G) Pk(G) 的定义可得:
(1) 若 k < χ ( G ) k<\chi(G) k<χ(G),则 P k ( G ) = 0 P_k(G) = 0 Pk(G)=0; χ ( G ) = min { k ∣ P k ( G ) ≥ 1 } \chi(G)=\min\left\{k|P_k(G)\geq1\right\} χ(G)=min{k∣Pk(G)≥1}
(2) 若 G G G 为 n n n 阶空图,则 P k ( G ) = k n P_k(G)=k^n Pk(G)=kn。
(3) P k ( K n ) = k ( k − 1 ) … ( k − n + 1 ) P_k(K^n)=k(k-1)…(k-n+1) Pk(Kn)=k(k−1)…(k−n+1)。
(4) 若图 G G G 含有 n n n 个孤立点,则 P k ( G ) = k n P k ( G ′ ) P_k(G) = k^nP_k(G') Pk(G)=knPk(G′),其中 G ′ G' G′ 是 G G G 去掉 n n n 个孤立点后所得的图
(5) 若图 G G G 有环或有重边,则去掉环并将重边用单边代替之后所得的图的 k k k 着色数目与原图一样。(这是因为研究图的着色时,涉及的是点与点是否邻接,并不涉及两点的邻接方式)
(二)、色多项式的两种求法
1、递推计数法
定理1 设 G G G为简单图,则对任意 e ∈ E ( G ) e\in E(G) e∈E(G) 有:
P k ( G ) = P k ( G − e ) − P k ( G • e ) P_k(G)=P_k(G-e)-P_k(G•e) Pk(G)=Pk(G−e)−Pk(G•e)


推论: 设 G G G是单图, e = u v e=uv e=uv 是 G G G 的一条边,且 d ( u ) = 1 d(u)=1 d(u)=1,则:
P k ( G ) = ( k − 1 ) P k ( G − u ) P_k(G)=(\text{k}-1)P_k(G-u) Pk(G)=(k−1)Pk(G−u)



通过加边变为完全图,加边规则为:任意连接两个顶点 + 将两个顶点收缩;通过减边变为空图,减边规则为:任意删掉某条边 - 将这条边的两点收缩
一般,对于具有 n 个点 m 条边的图,当 m ≤ 1 2 C ( n , 2 ) m ≤ \frac{1}{2}C(n, 2) m≤21C(n,2) ,宜用减边方法
注意: 在变换的过程中,出现环则去掉,出现平行边则合并为一条边

2、理想子图计数法
(1) 预备知识
定义1: 设 H H H是图 G G G的生成子图(包含所有顶点)。若 H H H的每个分支均为完全图,则称 H H H是 G G G的一个理想子图。用 N r ( G ) N_r (G) Nr(G)表示 G G G的具有 r r r 个分支的理想子图的个数。(有 n n n 个顶点就对应 n n n 个 N r ( G ) N_r (G) Nr(G))
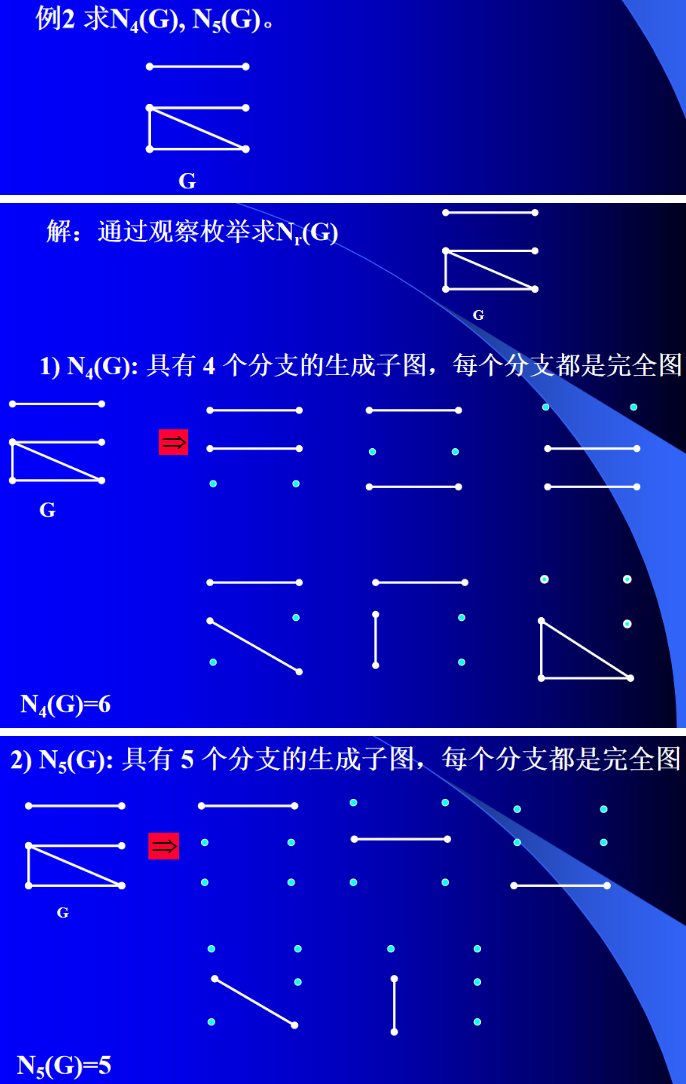
定理2 设 q r ( G ) q_r(G) qr(G)表示将单图 G G G的顶点集合 V V V划分为 r r r 个不同色组的色划分个数,则:
q r ( G ) = N r ( G ‾ ) , ( 1 ≤ r ≤ ∣ V ∣ ) q_r(G){=}N_r(\overline{G}),(1{\leq}r{\leq}|V|) qr(G)=Nr(G),(1≤r≤∣V∣)
证明: 一方面,设 G G G的任一 r r r色划分为: { V 1 , V 2 , … , V r } \{V_1, V_2,…,V_r\} {V1,V2,…,Vr}。于是,对于 1 ≦ i ≦ r 1≦i≦r 1≦i≦r, G ‾ [ V i ] \overline{G}\left[V_i\right] G[Vi] 是 G ‾ \overline{G} G 的完全子图。
因为 V i ∩ V j = Φ ( i ≠ j ) V_i ∩ V_j = Φ (i≠j) Vi∩Vj=Φ(i=j), 所以 G ‾ [ V i ] \overline{G}\left[V_i\right] G[Vi] 是 G ‾ \overline{G} G 的理想子图。
这说明: G G G 的任一 r r r 色划分必然对应 G ‾ \overline{G} G 的一个理想子图。容易知道,这种对应是唯一的;
另一方面,对于 G ‾ \overline{G} G 的任一具有 r r r个分支的理想子图,显然它唯一对应 G G G中一个 r r r色组。
所以,我们得到: q r ( G ) = N r ( G ‾ ) . . . . . ( 1 ≤ r ≤ ∣ V ∣ ) q_r(G){=}N_r(\overline{G}).....(1{\leq}r{\leq}|V|) qr(G)=Nr(G).....(1≤r≤∣V∣)
(2) 色多项式求法——理想子图法(期末考过)
上面定理2实际上给我们提供了色多项式的求法:用 k k k种颜色对单图 G G G正常着色,可以这样来计算着色方式数:色组为1的方式数+色组为2的方式数+…+色组为 n n n的方式数。即有如下计数公式: P k ( G ) = ∑ i = 1 n N i ( G ˉ ) [ k ] i , 其中, [ k ] i = k ( k − 1 ) ( k − 2 ) . . . ( k − i + 1 ) P_k(G)=\sum_{i=1}^nN_i(\bar{G})[k]_i,\text{其中,}[k]_i=k(k-1)(k-2)...(k-i+1) Pk(G)=i=1∑nNi(Gˉ)[k]i,其中,[k]i=k(k−1)(k−2)...(k−i+1)
定义2 : 设 G G G是单图,令 N i ( G ˉ ) = r i , [ k ] i = x i N_i(\bar{G})=r_i , [k]_i=x^i Ni(Gˉ)=ri,[k]i=xi 。称
h ( G , x ) = ∑ i = 1 n r i x i h(G,x)=\sum_{i=1}^nr_ix^i h(G,x)=i=1∑nrixi
为图 G G G的伴随多项式。
于是,求 P k ( G ) P_k(G) Pk(G)就是要求出 G ‾ \overline{G} G 的伴随多项式。

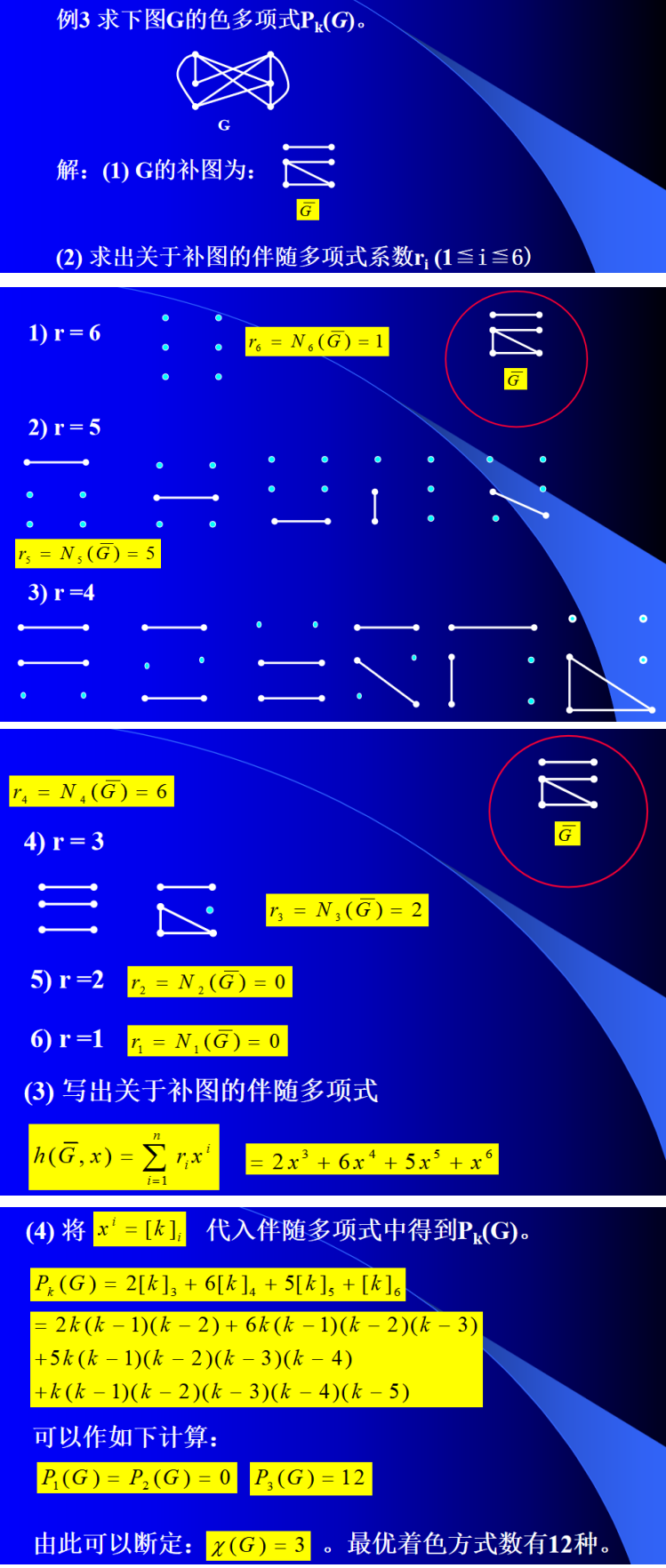
使用理想子图法求色多项式,还可以通过如下定理进行改进。
定理3 若 G G G有 t t t个分支 H 1 , H 2 , … H t H_1,H_2,…H_t H1,H2,…Ht, 且 H i H_i Hi的伴随多项式为 h ( H i , x ) , i = 1 , 2 , … , t h(H_i, x), i=1,2,…,t h(Hi,x),i=1,2,…,t, 则:
h ( G , x ) = ∏ i = 1 t h ( H i , x ) h\left(G,x\right)=\prod_{i=1}^{t}h\left(H_{i},x\right) h(G,x)=i=1∏th(Hi,x)
该定理说明,在求 G ‾ \overline G G 的伴随多项式时,可以分别求出它的每个分支的伴随多项式,然后将它们作乘积。

求出了色多项式,可以由多项式推出点色数。但是,求色多项式的计算量是很大的。递推方法是指数类计算量,而理想子图法中主要计算量是找出所有理想子图,这也不是多项式时间算法。
(三)、色多项式的性质(了解即可)
定理4 n n n阶单图 G G G的色多项式 P k ( G ) P_k(G) Pk(G)是常数项为 0 0 0的首 1 1 1整系数多项式,且各项系数符号正负相间。



这篇关于【图论及其运用 — 电子科技大学】(七)第七章 图的着色的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!