点积专题
【Python机器学习】NLP分词——利用分词器构建词汇表(二)——点积
在自然语言处理中将会有多处用到点积,点积也被称为内积,这是因为两个向量(每个向量中的元素个数)或矩阵(第一个矩阵的行数和第二个矩阵的列数)的“内部”维度必须一样,这种情况下才能相乘。这个关系数据库表的内连接操作很相似。 点击也被称为标积,因为其输出结果是个单独的标量值。这使其有别于叉积这个概念,后者的输出结果是一个向量。显然,这些名称体现了标识符的形状,在正式数学符号当中,标积用“”表示,叉积用
CUDA C编程:第一个程序 向量相加点积
我的电脑没有装CUDA,所以使用租了带GPU的云服务器,然后使用vscode SSH远程连接云服务器。云GPU使用的是智星云,0.8元/h。 智星云 可以使用nvcc --version查看系统中安装的CUDA版本。 然后写第一个CUDA程序,两个向量相加结果给到第三个向量 #include <cuda_runtime.h>#include <iostream>#define CHE
【NumPy】 之常见运算(min、max、mean、sum、exp、sqrt、sort、乘法、点积、对象拼接/切分)
____tz_zs 之前把 numpy 资料写在了同一篇博客里,发现非常难以查阅,于是按功能切分开来。 https://blog.csdn.net/tz_zs/article/details/73929778 https://blog.csdn.net/tz_zs/article/details/80773612 https://blog.csdn.net/tz_zs/article/det
学习transformer模型-矩阵乘法;与点积dot product的关系;计算attention
矩阵乘法: 1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。 Ankie的评论:一个人是站着的,一个人是躺着的,站着的高度=躺着的长度。 在计算attention的时候,因为QK是一样的矩阵,所以必须把K转置(躺下),才能相乘。 2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。 3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与
线性代数笔记3——向量2(点积)
什么是点积 如果A和B都是n维向量,这样定义点积: 点积结果是标量。 点积的几何意义是A和B的模乘以二者的夹角正余玄: 在几何意义中,点积同时包含了向量的长度和夹角信息。 代数表达和几何表达是等价的。 用余玄定理解释几何意义 余玄定理是这样说的:已知三角形的两边和夹角,可以知道第三边的长度。根据该定理:
不明白点积的几何意义
不明白点积的几何意义 在网上搜了很多资料,都说两个向量A和B的点积的几何意义是A到B的投影,我是想不明白,根据点积的定义 A.B = |A||B|cos x, x 是A和B之间的夹角 这里,我们看到|A|cos x的确是向量A投影在向量B上的长度,但是它还要乘上B的长度呀,这样点积的值不是单纯的投影,请问各位向量A在B上投影长度乘上B的长度,如果是物理上的力和位移,这个量不难理解,它就是功,但几
【易混区分】 tensor张量 Numpy张量的各种矩阵乘法、点积的函数对比 (dot, multiply,*,@matmul)
文章目录 1 矩阵运算基本概念1.1 点积1.2 矩阵乘法 2 dot()3 multiply() 和 *4 matmul和@ 1 矩阵运算基本概念 1.1 点积 又称为数量积、标量积(scalar product)或者内积(inner product) 它是指实数域中的两个向量运算得到一个实数值标量的二元运算。也就是对应元素的位置相乘 举例: 对于向量 a = ( x
Python 什么是点积注意力机制;点击注意力机制代码实现;Dot-Product Attention代码实战;超详细代码实现点积注意力
1.点积注意力机制简介 点积注意力机制(Dot-Product Attention)是一种常用的注意力机制之一,通常与Seq2Seq模型中的自注意力(Self-Attention)机制一起使用。它用于计算查询(Query)和键(Key)之间的相关性,并利用相关性来加权求和值(Value)。 点积注意力机制可以分为三个主要步骤: 1.1查询、键和值的线性变换
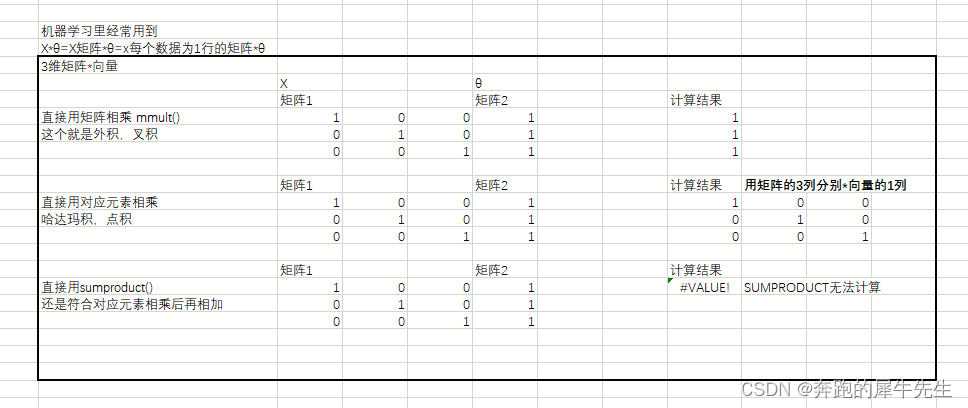
线性代数的学习和整理23:用EXCEL和python 计算向量/矩阵的:内积/点积,外积/叉积
目录 1 乘法 1.1 标量乘法(中小学乘法) 1.1.1 乘法的定义 1.1.2 乘法符合的规律 1.2 向量乘法 1.2.1 向量:有方向和大小的对象 1.2.2 向量的标量乘法 1.2.3 常见的向量乘法及结果 1.2.4 向量的其他乘法及结果 1.2.5 向量的模长(长度) 模长的计算公式 1.2.6 距离 2 向量的各种乘法 2.1 向量的标量乘法(
B2091 向量点积计算 题解
题目分析 其实这里只用一个循环就能解决这个问题了,在输入第二个数列时,每输入一个数就计算它与与之对应的第一数列的数的乘积,然后加入计数器,计数器内的数便是结果。 代码实现 #include<bits/stdc++.h> using namespace std; int n,a[1010],b[1010],sum; int main(){ cin>>n; for(int i=1;
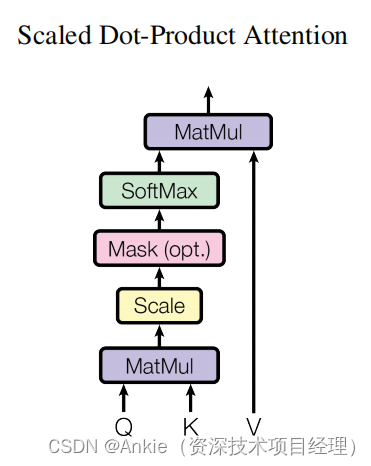
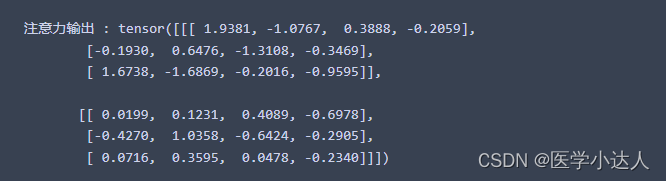
了解PyTorch中的缩放点积注意力及演示
torch.nn.functional.scaled_dot_product_attention 函数在 PyTorch 框架中用于实现缩放点积注意力(Scaled Dot-Product Attention)。这是一种在自然语言处理和计算机视觉等领域常用的注意力机制。它的主要目的是通过计算查询(query)、键(key)和值(value)之间的关系,来决定我们应该在输入的哪些部分上聚焦。 函数
注意力机制:点积、通用、缩放点积、拼接、相加
自 然 语 言 推 理 (Natural Language Inference,NLI)任务中相对应的 句子等。如果将下游任务抽象成查询(query),就可 以归纳出注意力机制的通用形式,即将源文本看成 是键-值对序列,用K=(k1,…,kN )和V=(v1,…,vN )分 别表示键序列和值序列,用 Q=(q1,…,qM)表示查询序列,那么针对查询的注意力可以被描述为键-值对序列在该查询上的映射
图论——随机图与随机点积图
一、随机图 在数学领域中,随机图random graph是指图上的概率分布的一般术语。随机图可以简单地用概率分布表示,也可以用生成它们的随机过程表示。从数学的角度来看,随即图可以用来回答有关典型图的性质的问题。在所有需要对图复杂网络进行建模的领域都能看到它的实际应用——由于它反映了在不同领域遇到的不同类型的复杂网络,许多随机图模型就此被人们所熟知。在数学上随机图既合乎完全指的是ER随机图模型(E
1.2 向量的长度与点积
一、向量的点积 两个向量 v = ( v 1 , v 2 ) \boldsymbol v=(v_1,v_2) v=(v1,v2) 与 w = ( w 1 , w 2 ) \boldsymbol w=(w_1,w_2) w=(w1,w2)的点积或内积是数字 v ⋅ w \boldsymbol v\cdot\boldsymbol w v⋅w: v ⋅ w = v 1 w 1 +
每日一题 1458两个子序列的最大点积
题目 题目 给你两个数组 nums1 和 nums2 。 请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。 数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。 示例 1: 输入:nums1 = [2,1,-2