本文主要是介绍图论——随机图与随机点积图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、随机图
在数学领域中,随机图random graph是指图上的概率分布的一般术语。随机图可以简单地用概率分布表示,也可以用生成它们的随机过程表示。从数学的角度来看,随即图可以用来回答有关典型图的性质的问题。在所有需要对图复杂网络进行建模的领域都能看到它的实际应用——由于它反映了在不同领域遇到的不同类型的复杂网络,许多随机图模型就此被人们所熟知。在数学上随机图既合乎完全指的是ER随机图模型(Erdős–Rényi model)。在其他情况下,任何图形模型都可以称为随机图。
二、什么是ER随机图模型?
ER随机图模型(Erdős–Rényi model)有两个。其名字源于最早提出上述模型之一的数学家保尔·厄多斯(Paul Erdős)和阿尔弗烈德·瑞利(Alfréd Rényi),他们在1959年首次提出了其中一个模型,几乎在同时期,埃德加·吉尔伯特(Edgar Gilbert)独立提出了另外一个模型。
在厄多斯和瑞利的模型中,给定节点和边数情况下产生出任意一种情况的概率是相同的;在吉尔伯特的模型中,每个连边存在与否有着固定的概率,与其他连边无关。在概率方法中,这两种模型可用来证明满足各种性质的图的存在,也可为几乎所有图的性质提供严格的定义。如果这里不太清楚,下面我们对这两种模型进行举例的对比。
三、模型
1.吉尔伯特模型
给定n个孤立的点,在它们之间随即添加连续的边,这样就得到一个随机图。这个领域研究的目的是确定在什么阶段图形的特殊性质可能会出现。不同的随机图模型产生不同的概率分布。最常见的研究是由埃德加·吉尔伯 为特提出的,表示G(n,M),其中每个可能的边独立出现的概率为0<p<1。获得任意一个m边随机图的概率是pm(1-m)(N-m),N代表所有n可能组成的边数量,
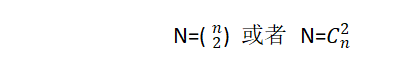
pm代表有m条边的概率,(1-m)(N-m)代表剩下的(N-m)条边不出现的概率。
2.Erdős–Rényi model模型
一个相关性强的模型,Erdős–Rényi model模型表示G(n,M),给每一个正好有m条边的图赋予等概率。当 0≤M≤N 时,G(n,M)具有
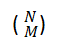
个元素,且每个元素都以概率
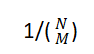
出现。后一个模型可以看作是随机图过程 G ‾ \overline{G} G n在某个特时间(M)的一个快照,这个时间(M)是从n个顶点开始没有边的一个随机过程,每个均匀地从缺失的边集中选择一个新的边。
如果我们从一个无限的顶点集合开始,然后让每个可能的边以概率 0<p<1 独立出现,那么我们得到一个对象G称为无限随机图Infinite Graph。除了在p=0或1的情况下,这样的G在大多数情况下肯定具有以下性质:
- 在v中,给定任何n+m个元素,a1,…,an,b1,…,bm∈V中有一个顶点c,它与每个a1到an相邻,并且不与任何b1,…,bm相邻。
结果表明如果顶点集是可数的,那么在同构Isomorphism意义下,只有一个图具有这个性质,即Rado图。因此,任何可数无限随机图几乎可以肯定是Rado图,由于这个原因,有时被称为随机图。然而,对于不可数图Uncountable Graph类似的结果是不正确的,不可数图中有许多不同构图Nonisomorphic Graph满足上述性值。
另一个模型,概括了吉尔伯特的随机图模型,是随机点积模型Random Dot-product Model。一个随机点积图Random Dot-product Model将每个顶点与一个实向量相关联。任意顶点u和v之间的边 uv 的概率是它们各自向量的点积 u·v的某个函数。
网络转移矩阵(Network Probability Matrix)通过边概率对随机图进行建模,这些边概率代表给定的边存在一个特定的时间段的概率。这个模型可以扩展到有向和无向,加权和无权,以及静态或者动态的图形结构。
对于M≃pN,其中N是可能的最大边数,两个最广泛使用的模型,G(n,M)和G(n,p)在大多数情况下是可互换的。

随即正则图(Random Regular Graph)是一种特殊情况,其性质可能与一般随机图不同。
四、两种ER随机图模型的简单比较
1.Erdős–Rényi model模型:给定节点数量和边数的ER随机图模型G(n,M)
例如,在G(3,2)模型中,三个顶点和两个边可以构成三个可能的图,每一个都以1/3的概率包含在内。
2.Erdős–Rényi model模型:具有固定节点和连边概率的的ER随机图模型G(n,p)
这种方法是通过随机选取连接节点的方式来产生图。每个边产生的可能都是一个不受其他边影响的概率,该模型中的参数p表示随机两点之间产生边的概率,p可以看作是一个加权函数。当p从0增加到1时,模型越来越多地包含具有更多边的图。拥有n个结点、M个连边的所有图被输出的概率都是相同的。
这篇关于图论——随机图与随机点积图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!