大顶专题
【C++】大顶堆(最大堆)手工模拟优先队列
前言 本文采用结构体重载比较运算符的方式进行大根堆的建立,算法逻辑类似 S T L STL STL的 p r i o r i t y _ q u e u e priority\_queue priority_queue。 结构体 堆本身就是一颗完全二叉树,所以本身用数组存储就行。 int heap[N]; 输入堆 for(int i=1;i<=n;i++} cin>>heap[i];
堆:什么是大顶堆,什么是小顶堆,堆排序,代码实现堆排序
堆排序代码 using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Threading.Tasks;namespace 堆排序___顺序存储{class Program{static void Main(string[] arg
wikioi 2573 大顶堆与小顶堆并用
题目描述 Description 我们使用黑匣子的一个简单模型。它能存放一个整数序列和一个特别的变量i。在初始时刻,黑匣子为空且i等于0。这个黑匣子能执行一系列的命令。有两类命令: ADD(x):把元素x放入黑匣子;GET:把i加1的同时,输出黑匣子内所有整数中第i小的数。牢记第i小的数是当黑匣子中的元素已非降序排序后位于第i位的元素。 下面的表6_4是一个11个命令的例子:
wikioi 1052 大顶堆
题目描述 Description 王钢是一名学习成绩优异的学生,在平时的学习中,他总能利用一切时间认真高效地学习,他不但学习刻苦,而且善于经常总结、完善自己的学习方法,所以他总能在每次考试中得到优异的分数,这一切很大程度上是由于他是一个追求效率的人。 但王钢也是一个喜欢玩的人,平时在学校学习他努力克制自己玩,可在星期天他却会抽一定的时间让自己玩一下,他的爸爸妈妈
代码随想录笔记|C++数据结构与算法学习笔记-栈和队列(〇)|stack、queue、单调队列和优先级队列(priority_queue)、大顶堆和小顶堆
文章目录 stack容器stack 基本概念常用接口构造函数赋值操作数据存取大小操作 queue容器queue常用接口构造函数:赋值操作数据存取大小操作 单调队列定义实现代码实现 基本应用一:滑动窗口思路与算法 优先级队列定义大顶堆(最大堆)、小顶堆(最小堆) 实现基本操作`push`和`emplace` 基本应用一:滑动窗口思路与算法 stack容器 stack 基本
python使用heapq实现小顶堆(TopK大)/大顶堆(BtmK小)
参考链接 https://www.coder4.com/archives/3844 求一个数列前K大数的问题经常会遇到,在程序中一般用小顶堆可以解决,下面的代码是使用python的heapq实现的小顶堆示例代码: # !/usr/bin/env python# -*- coding:gbk -*-import sysimport heapqclass TopKHeap(object)
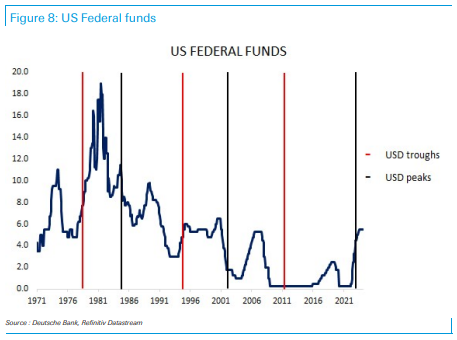
德银:历次美元大顶有何异同?
在全球外汇市场中,美元的周期性巅峰一直是投资者关注的焦点。 动荡时期,投资者往往会将美元作为“避风港”,随着美联储降息前景充满不确定性,美元汇率的走势也变得愈发模糊——是否即将见顶? 2月29日,德意志银行发布报告分析了历史上美元周期顶峰的特征,发现有1985年和2002年两次显著的“美元大顶”,随后由盛转衰,推动美元强势的因素包括美元的低估值起点和美国增长“例外论”,其中宏观政策变化和技术创
【优先级队列(大顶堆 小顶堆)】【遍历哈希表键值对】Leetcode 347 前K个高频元素
【优先级队列(大顶堆 小顶堆)】【排序】Leetcode 347 前K个高频元素 1.不同排序法归纳2.大顶堆和小顶堆3.PriorityQueue操作4.PriorityQueue的升序(默认)与降序5.问题解决:找前K个最大的元素 :踢走最小的(堆顶的),加入比堆顶大的,最终就是最大的K个6.问题解决:找前K个最小的元素 :维护一个小顶堆,最后从堆顶依次弹出K个,最终就是最小的K个 题
数据结构:大顶堆、小顶堆
堆是其中一种非常重要且实用的数据结构。堆可以用于实现优先队列,进行堆排序,以及解决各种与查找和排序相关的问题。本文将深入探讨两种常见的堆结构:大顶堆和小顶堆,并通过 C++ 语言展示如何实现和使用它们。 一、定义 堆是一种完全二叉树。完全二叉树的定义:所有节点从上往下,从左往右的依次排列,不能有空位置,是为完全二叉树。 下面是完全二叉树和不完全二叉树的示意图: 大顶堆: 根节点(堆顶元素
大顶堆(Max Heap)
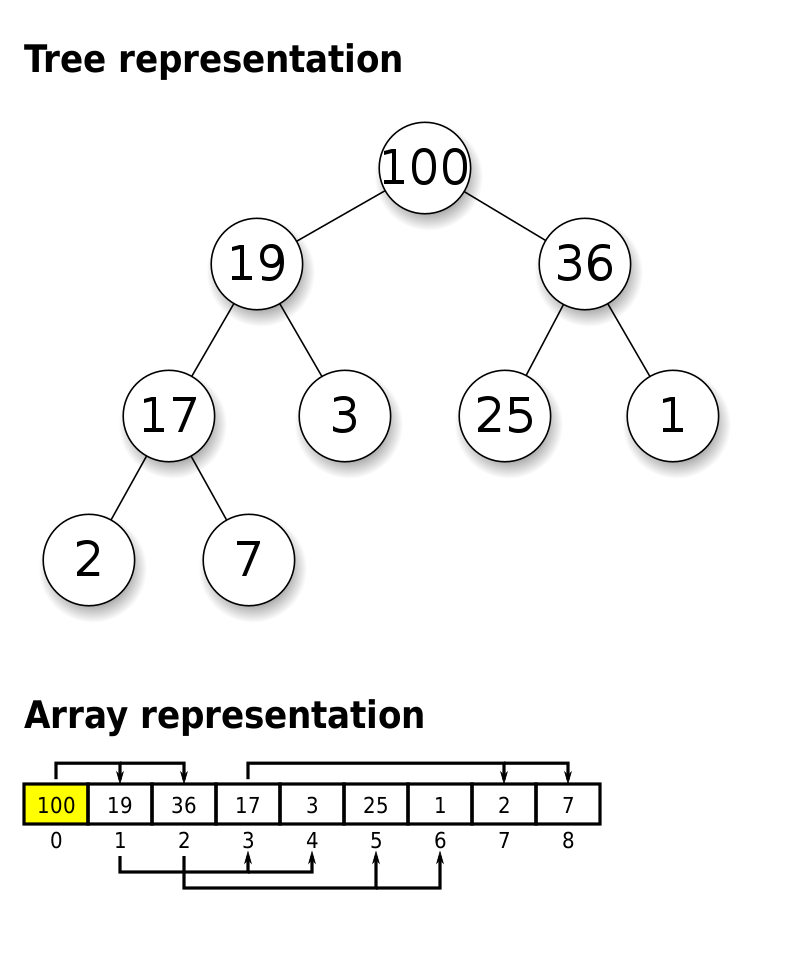
大顶堆(Max Heap) 大顶堆是一种特殊的树形数据结构,它满足以下性质: 它是一个完全二叉树:除了最底层外,每一层都被完全填满。在最底层,所有的元素都应该尽可能地靠左排列。 每个节点的值都大于或等于其子节点的值。这就是为什么它被称为大顶堆。 下面是一个大顶堆的示例: 上图中,根节点(100)是所有节点中的最大值。同样,每个父节点的值都大于或等于其子节点的值。 好的,下面我将
Java PriorityQueue实现大顶堆
Java中PriorityQueue通过二叉小顶堆实现,可以用一棵完全二叉树表示。PriorityQueue位于Java util包中,实际上这个队列就是具有“优先级”。既然具有优先级的特性,那么就得有个前后排序的“规则”。所以其接受的类需要实现Comparable 接口。该队列线程安全,不允许null值,入队和出队的时间复杂度是O(log(n))。 PriorityQueue 默认是小根堆,大
大顶堆、小顶堆及其建堆过程、堆排序
定义 按照堆的特点可以把堆分为大顶堆和小顶堆。 大顶堆:每个结点的值都大于或等于其左右孩子结点的值; 小顶堆:每个结点的值都小于或等于其左右孩子结点的值。 (堆的这种特性非常的有用,堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素) 我们用简单的公式来描述一下堆的定义就是: 大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
力扣973. 最接近原点的 K 个点(java 排序法,大顶堆法)
Problem: 973. 最接近原点的 K 个点 文章目录 题目描述思路解题方法复杂度Code 题目描述 给定一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点,并且是一个整数 k ,返回离原点 (0,0) 最近的 k 个点。 这里,平面上两点之间的距离是 欧几里德距离( √(x1 - x2)2 + (y1 - y2
【每日一题Day361】LC2558从数量最多的堆取走礼物 | 大顶堆
从数量最多的堆取走礼物【LC2558】 给你一个整数数组 gifts ,表示各堆礼物的数量。每一秒,你需要执行以下操作: 选择礼物数量最多的那一堆。如果不止一堆都符合礼物数量最多,从中选择任一堆即可。选中的那一堆留下平方根数量的礼物(向下取整),取走其他的礼物。 返回在 k 秒后剩下的礼物数量*。* 思路 使用大顶堆存放所有礼物,每次将堆顶元素移出,并将其平方根放入堆中,最后求出堆中剩
大顶堆在Java中的一种优雅实现
既然小顶堆已经实现出来,那么同理大顶堆也顺理成章实现出来,只需稍微改动几个关键部分的代码。 /*** 大顶堆/最大堆实现* * @author stephenshen**/public class MaxHeap {// 堆得存储结构:数组private int[] data;/*** 构造方法:传入一个数组,并转换为一个最大堆* * @param data*/public MaxHeap(i
堆排序;大顶堆、小顶堆
堆排序 基本介绍 堆排序基本思想 堆排序步骤图解 在第二个步骤中,将节点6和它的两个左右节点比较大小,发现右节点最大,所以将节点6和节点9进行交换,如图所示,数组相应位置的值也交换 总结 代码实现 """ 堆排序 """class HeapSort:def __init__(self, arr):self.arr = arrd
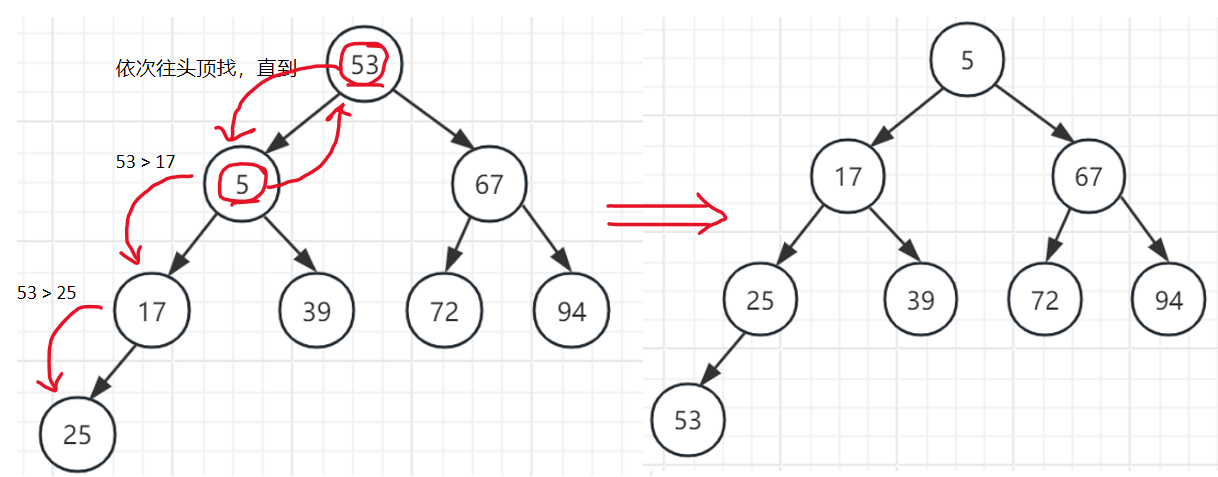
堆专题2 向上调整构建大顶堆
题目: 样例: 输入 63 2 6 5 8 7 输出 8 6 7 2 5 3 思路: 向上调整,就是从叶子结点开始 往 根节点 往上面调整,操作与 向下调整 操作类似,只是不用判断左右孩子,由于我们是从叶子结点开始 往 根节点 往上面调整,所以不用考虑左右孩子。 代码详解如下: #include <iostream>#include <vector
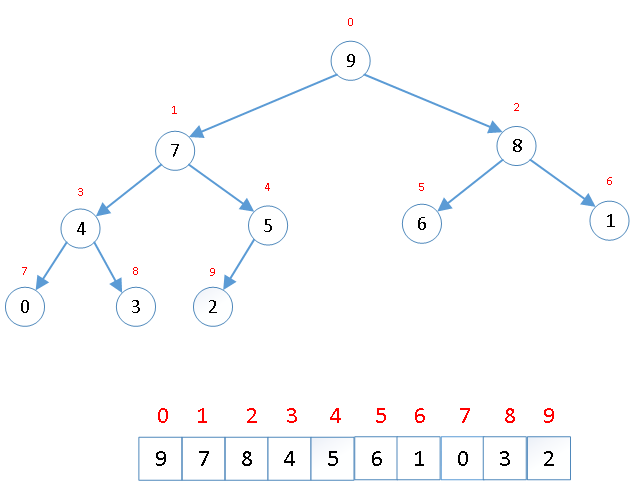
堆专题1 向下调整构建大顶堆
题目: 样例: 输入 63 2 6 5 8 7 输出 8 5 7 3 2 6 思路: 堆,是一颗完全二叉树,树中每个节点的值都不小于(或不大于)其左右孩子结点的值。 其中, 父结点大于或者等于孩子结点的值,称为大顶堆。 父结点小于或者等于孩子结点的值,称为小顶堆。 由于堆,是一颗完全二叉树,所以,我们可以将该完全二叉树压缩成 一维数组进行存储。 其