堆排序（大顶堆）

本文主要是介绍堆排序（大顶堆），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一：堆
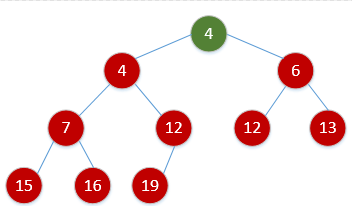
堆可以看做一个完全二叉树，同时该完全二叉树满足双亲结点大于等于孩子结点（大顶堆），或者双亲结点小于等于孩子结点（小顶堆）。
二：堆排序（以大顶堆为例）
大顶堆产生顺序序列，小顶堆产生逆序序列。
已知序列[a0,a1,…,an]。测试序列为{5，9，3，7，6，5}；

a）将序列初始化，从最后面的非叶子结点开始调整产生大顶堆。

b）将a0和an交换，a0到an-1（无序区）不满足大顶堆则重新调整，an为有序区。（a0处保存的是无序区生成的子堆中的最大值。）

c）进行n-1次(b)步的调整，有序区将包含n-1个有序元素，最后一个元素即为最小元素。排序完成。

#include<iostream>
using namespace std;void swap(int *a, int *b)
{int temp = *a;*a = *b;*b = temp;
}void HeadAdjust(int a[], int i, int length)
{int lChild = 2*i+1;int rChild = 2*i+2;int max = i;if(i<=(length-1)/2){if(lChild<=length-1 && a[lChild]>a[max]){max = lChild;}if(rChild<=length-1 && a[rChild]>a[max]){max = rChild;}if(max != i){swap(&a[max],&a[i]);HeadAdjust(a,max,length);}}
}void InitHead(int a[], int length)
{for(int i=(length-1)/2;i>=0;i--){HeadAdjust(a,i,length);}
}void HeadSort(int a[], int length)
{InitHead(a,length);
//  for(int i=0; i<length; i++)
//  {
//      cout<<a[i]<<" ";
//  } 
//  cout<<endl;for(int i=length-1;i>0;i--){swap(&a[0],&a[i]);HeadAdjust(a,0,i);
//      for(int i=0; i<length; i++)
//      {
//          cout<<a[i]<<" ";
//      } 
//      cout<<endl;} 
}
int main()
{int a[100] = {0};int length=0;cin>>length;if(length>0){for(int i=0; i<length; i++){cin>>a[i];}HeadSort(a,length);for(int i=0; i<length; i++){cout<<a[i]<<" ";}cout<<endl;}return 0;
} 

运行结果：

这篇关于堆排序（大顶堆）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---