堆排序算法剖析（基于Java）

本文主要是介绍堆排序算法剖析（基于Java），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

什么是堆结构？
堆排序的关键是构造堆结构，首先谈一下堆结构的定义，堆结构是一种树结构，准确地说是一个完全二叉树，完全二叉树的定义在这里就不多赘述了，百度知道。
按照排序顺序，堆结构可以分为两种：
1.按照从小到大的顺序排序，要求非叶节点的数据要大于或等于其左、右子节点的数据。
2.按照从大到小的顺序排序，要求非叶节点的数据要小于或等于其左、右子节点的数据。
本文以从小到大的顺序为例进行介绍。
堆排序的过程
一个完整的堆排序需要经过两个过程：构建堆结构和堆排序输出。
首先对堆结构的建立进行分析，
第一步：将原始的无序数据放到一个完全二叉树的各个节点中，具体实现方法是使用Math类下的random（）方法随机生成n个数放置到大小为n的数组中。如此我们便抽象地构造了一个完全二叉树：

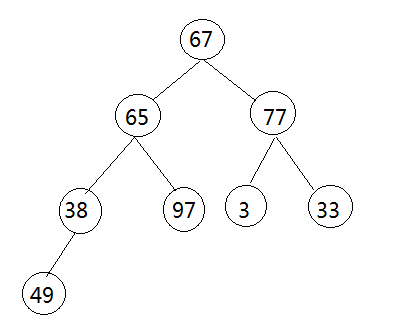
第二步：有完全二叉树的下层向上层逐层对父子节点的数据进行比较，使父节点的数据大于子节点的数据，循环递归直到所有节点满足堆结构的条件为止，过程比较简单，下面附有程序和图示：
构建堆结构

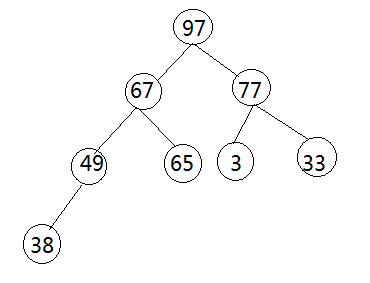
堆结构示意图
第三步：第三步也是最难理解的一步，这里我将自己非权威的理解分享给大家，拒绝晦涩的“学术”描述，接下来我们根据程序进行分析，程序才是算法最简洁直观的呈现：

利用堆结构进行排序
首先来看最外层的for()循环，因为我们要排序的是所有节点的数据，所以这是一个整体的遍历，也就是a[1]到a[n-1]，那么，为什么不是a[0]到a[n]呢，我们知道数组a[i]中下标i是从0开始的，所以a[n]固然不存在，那么a[0]呢，因为循环到最后只剩下a[1]和根节点a[0]，根据堆结构的定义，必然有a[0]>a[1]，接下来经过后面三条交换语句自然将最小的a[1]放到了a[0]（根节点）的位置，排序完成。
我们看经过三条交换语句后，有个k的初始化，令k=0我们马上想到的是a[k]是指向根节点的。
接下来进入while()循环，我们对照前面堆结构的建立代码中while()循环可以很容易的发现它们其实是完成了一样的功能，对，是构建堆结构，而从前面堆结构的建立我们可以观察到两者的区别就在while语句上：
第二步中while（2*i+1<n）这里n是固定值，拿到本例来说也就是n为8；
第三步中while（2*k+1<i）这里的i是变化值，因为有for(i=n-1;i>0;i++)

*是不是
有点晕
缓一缓。。。。。。。。。。。。
、
、
、*

先拿第二步来说，第二步主要任务是建立堆结构，构建过程可以涉及到任何元素，包括最后的叶子节点a[n-1]，但是第三步就有所不同了，进入for()后第一次循环就把数值最大的根节点a[0]放到了最后的a[n-1]位置（这么做的原因很简单，我们要实现从小到大排序，自然要把最大的数放到最后）。
好了，到这里大家可能猜到了，接下来，我们要在倒数第二个位置（也就是a[n-2]的位置）放置倒数第二大的数（原谅我这么老土的描述，实在是易于理解），那么倒数第一个数也就是我们刚刚通过与根节点交换过去的整个数组中的最大值是不是就不用管了，对头，我们直接把它踢掉，只关注剩下的n-1个数，再构建堆找最大的数放到最后的位置（第二次是a[n-2]，第三次是a[n-3]……），所以第三步中的for(i=n-1;i>0;i++)和while（2*k+1<i）也就捎带理解了。

好吧，编程工作完成了，排序结果不言而喻，我也不再画蛇添足了。

附录

package 堆排序;public class Example {static final int SIZE=10;private static void heapSort(int a[],int n) {int i,j,h,k;int t;for(i=n/2-1;i>=0;i--){while(2*i+1<n){     //第i个节点不是叶子节点j=2*i+1;if((j+1)<n){      //第i个节点有右子树if(a[j]<a[j+1])j++;}  //将j指向i右子节点的下标if(a[j]>a[i]){       //子节点大于父节点t=a[i];a[i]=a[j];a[j]=t;       //交换父子节点i=j;          //将j赋给i，以便退出while()循环}else break;}}System.out.print("源数据构成的堆： \n");for(h=0;h<n;h++){System.out.print(" "+a[h]);   //输出构建好的堆结构                                                                             }               System.out.println("\n");for(i=n-1;i>0;i--){ t=a[0];          a[0]=a[i];a[i]=t;      //将根节点a[0]与排在最后位置的叶子节点a[i]交换k=0;while(2*k+1<i){    j=2*k+1;if((j+1)<i){   if(a[j]<a[j+1])j++;}if(a[j]>a[k]){t=a[k];a[k]=a[j];a[j]=t;k=j;}else break;}}}public static void main(String[] args) {int[] shuzu=new int[SIZE];int i;for(i=0;i<SIZE;i++){shuzu[i]=(int)(100+Math.random()*(100+1));}System.out.println("排序前的数组为：");for(i=0;i<SIZE;i++){System.out.print(shuzu[i]+" ");}System.out.print("\n");heapSort(shuzu,SIZE);System.out.println("排序后的数组为:");for(i=0;i<SIZE;i++){System.out.print(shuzu[i]+" ");}System.out.println("");}}