本文主要是介绍堆排序;大顶堆、小顶堆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
堆排序
基本介绍
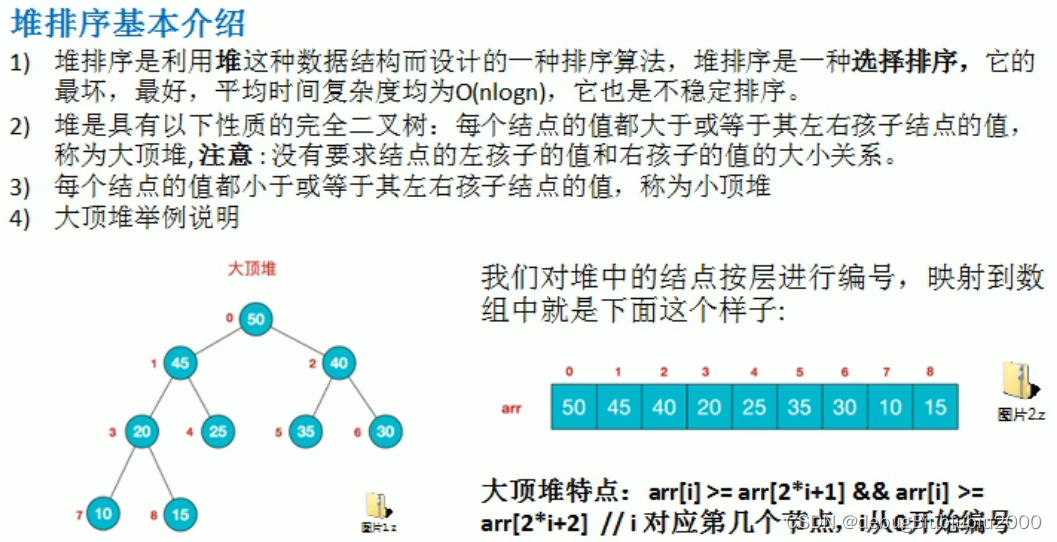

堆排序基本思想

堆排序步骤图解


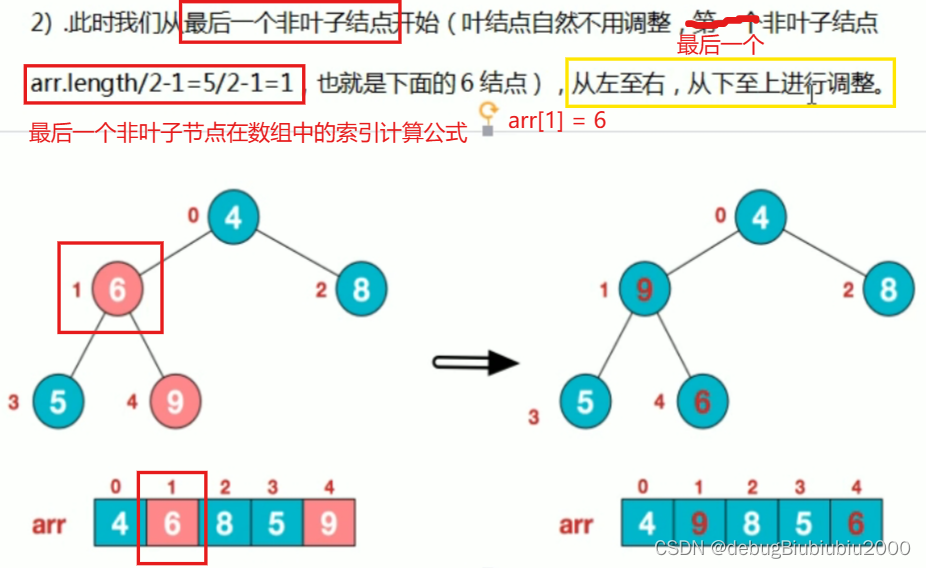
在第二个步骤中,将节点6和它的两个左右节点比较大小,发现右节点最大,所以将节点6和节点9进行交换,如图所示,数组相应位置的值也交换






总结

代码实现

""" 堆排序 """
class HeapSort:def __init__(self, arr):self.arr = arrdef adjust_heap(self, i: int, n: int):"""arr[i] 对应一个非叶子节点,adjust_heap()方法的作用就是将arr[i]这个非叶子节点下的所有子树构建成大顶堆即从该非叶子节点开始,它下面的子树都满足大顶堆的定义如图中的第一个非叶子节点arr[1] = 6,其对应的子树如下,构建之后变为如下6 9=>5 9 5 6arr=[4,6,8,5,9], i=1 => adjust_heap() => 构建之后得到arr=[4,9,8,5,6]下一次再调用adjust_heap():arr=[4,9,8,5,6], i=0 => adjust_heap() => 构建之后得到arr=[9,6,8,5,4]adjust_heap()是将非叶子节点对应的:param i: 表示非叶子节点在数组中的索引:param n: 表示构建大顶堆时的元素个数(即要对多少个元素进行构建大顶堆),m是逐渐减少的:return:"""temp = self.arr[i] # 保存非叶子节点的值k = 2 * i + 1 # k 为叶子结点的左子节点while k < n:# k + 1 = 2 * i + 1 + 1 = 2 * i + 2,即表示右子节点# self.arr[k]表示左子节点的值,self.arr[k+1]表示右子节点的值if k + 1 < n and self.arr[k] < self.arr[k + 1]:# 如果左子节点小于右子节点的值,让 k 指向右子节点k += 1 # => k = 2 * i + 2if self.arr[k] > temp: # 如果子节点(左/右子节点)大于父节点(非叶子结点)self.arr[i] = self.arr[k] # 把较大的值赋值给当前节点i = k # 让 i 指向 k 的位置else:breakk = k * 2 + 1 # 下一个左子节点,即左子节点的左子节点# 当循环结束后,已经在局部将以 i 为父节点的树的最大值放在了堆顶self.arr[i] = temp # 将 temp 值放到调整后的位置"""以上代码请结合图来理解!!!"""def heap_sort(self):"""讲一个数组(该数组是二叉树顺序存储之后的数组)构建为大顶堆:return:"""print("=======堆排序=======")print("排序前的数组:", self.arr)# self.adjust_heap(1, len(self.arr))# print("第一次调整后的数组:", self.arr) # [4, 9, 8, 5, 6]# self.adjust_heap(0, len(self.arr))# print("第二次调整后的数组:", self.arr) # [9, 6, 8, 5, 4]n = len(self.arr)# 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆i = n // 2 - 1 # 从第一个非叶子节点开始进行调整,即从左往右,从下往上进行while i >= 0:self.adjust_heap(i, n)i -= 1# 将堆顶元素与数组末尾元素交换,将最大元素“沉”到数组末尾# 重新调整堆结构,使其满足大顶堆或小顶堆的定义,然后继续交换堆顶元素与数组末尾元素# 反复执行直到整个序列有序j = n - 1while j > 0:# self.arr[0]为堆顶元素,self.arr[j]为数组末尾元素,将其交换temp = self.arr[j]self.arr[j] = self.arr[0]self.arr[0] = temp# 交换后重新调整堆结构,0表示从根节点开始,将整棵树进行调整self.adjust_heap(0, j)j -= 1print("排序后的数组:", self.arr)heap_sort = HeapSort([4, 6, 8, 5, 9])
heap_sort.heap_sort()这篇关于堆排序;大顶堆、小顶堆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!