大顶堆、小顶堆

2024-02-21 00:28

文章标签 大顶小顶

本文主要是介绍大顶堆、小顶堆，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

堆

堆
- 堆的维护
- - 1.自我初始化
  - 代码
  - 2.插入时维护
  - 时间复杂度

代码如有误欢迎指出

本文是最近在整理排序算法的时候写到堆排序单拎出来写的，目前只有维护代码

堆

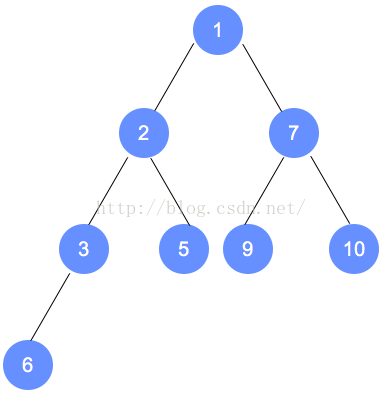
堆是一颗完全二叉树，同时保证所有双亲都比自己的孩子大（可以相等

堆的维护

使用数组存储，长度为 n+1，从 1 索引开始存储，对 $i$ ， $2 i$ 和 $2 i + 1$ 是孩子， $\frac{i}{2}$ 是双亲

1.自我初始化

把一个现有数组自我初始化为堆：
原理：
先把小的子树维护好，然后由小至大维护
从第二小的子树开始（最小的子树是叶子）
找到子树，维护就是看左右子树是否有应该当堆顶的（如小顶堆就是找是否有比双亲节点小的孩子）

实现：
索引值最大的第二小的子树是几？是 $\frac{n}{2}$ ！
注意，调整子树的堆顶之后有可能影响子树的子树，需要往下继续维护，直到叶子

维护小顶堆示例：
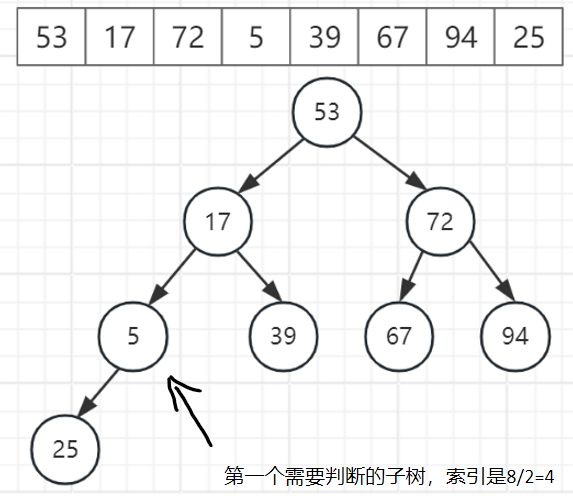
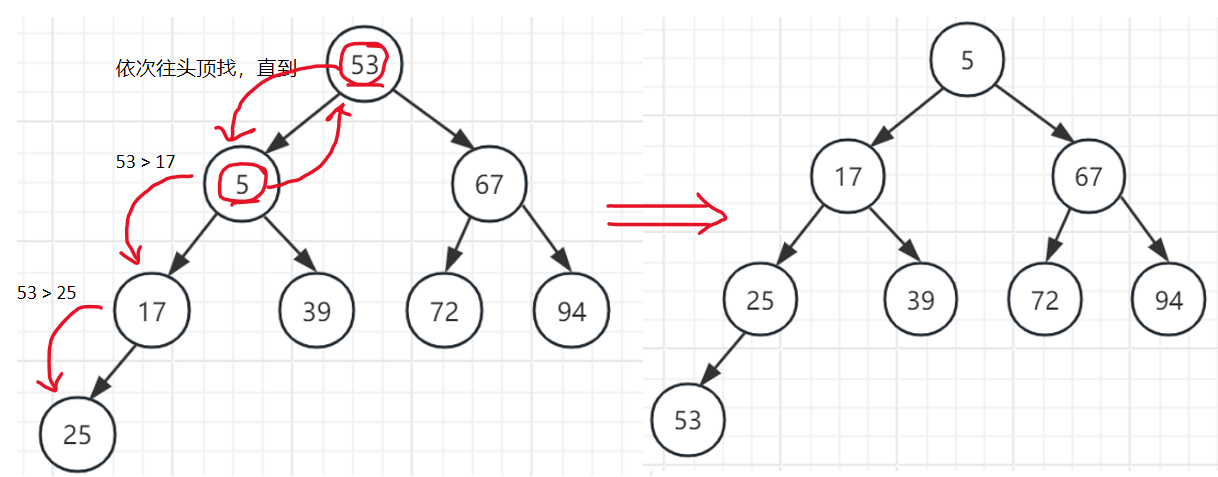
在这里插入图片描述

代码

/*测试样例1
8 
53 17 72 5 39 67 94 25
得到:
5 17 67 25 39 72 94 53
*/
/*测试样例2
9 
53 17 72 5 39 94 67 25 1
得到:
1 5 67 17 39 94 72 25 53
*/
#include <iostream>
using namespace std;
int nums[105];
int n;void adjustDown(int heap[],int i,int n)
{int child_p = 2 * i;    //i结点（在循环中是指对应调整的子树）的孩子的索引int parent = heap[i];   //本子树的根结点的值while (child_p<=n)      //保证双亲是有孩子结点的，叶子结点本身就是排好的堆，不需要调整{if (child_p + 1 <= n && heap[child_p + 1] < heap[child_p])   child_p++;//选中左右孩子中更小的和双亲作比较if (heap[child_p] < parent){heap[child_p / 2] = heap[child_p];//将孩子的值赋给父亲child_p *= 2;}else{break;}}heap[child_p/2] = parent;//这一步容易忘记！！！！就是赋回i结点的值！当然如果每次比较完用tmp去做交换就可以不用这么麻烦，我就是不想用tmp交换，因为那样有三次赋值，而这样写只有一次
}int main()
{//数组初始化cin >> n;for (int i = 1; i <= n; i++){cin >> nums[i];}//小顶堆初始化for (int i = n/2; i >=1; i--){adjustDown(nums, i, n);}//排序后展示for (int i = 1; i <= n; i++){cout << nums[i] << ' ';}cout << endl;
}

2.插入时维护

思路和自我初始化差不多，就是从下而上，从插入结点的双亲比较，往上找需要调整的每一个结点

/*测试样例1
8
53 17 72 5 39 67 94 25
得到:
5 17 67 25 39 72 94 53
*/
/*测试样例2
9
53 17 72 5 39 94 67 25 1
得到:
1 5 67 17 39 94 72 53 25(注意，这个和自我初始化的结果不一定一样)
*/
#include <iostream>
using namespace std;
int nums[105];
int n;void heapInsertAdjust(int heap[], int i)//尾部插入后做的调整
{int child = heap[i];    //最初插入的值，循环中做每次比较的孩子int parent_p = i / 2;   //循环中每次比较的双亲索引int lastParent_p = i;   //循环中最后一次赋给双亲的位置，默认不交换就是i原地（其实就是“上一个双亲”的位置，因为/2会默认向下取整，需要用这个标记while (parent_p >= 1){if (heap[parent_p] > child){heap[lastParent_p] = heap[parent_p];  //将双亲的值赋给孩子，继续往上找lastParent_p = parent_p;              //更新赋值位置parent_p /= 2;}else break;}heap[lastParent_p] = child;
}int main()
{//数组初始化cin >> n;for (int i = 1; i <= n; i++){int tmp;cin >> nums[i];heapInsertAdjust(nums, i);//插入的时候调整}//排序后展示for (int i = 1; i <= n; i++){cout << nums[i] << ' ';}cout << endl;
}