本文主要是介绍数据结构 小顶堆建堆过程 构建过程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【一】简介
- 最小堆是一棵完全二叉树,非叶子结点的值不大于左孩子和右孩子的值。本文以图解的方式,说明最小堆的构建、插入、删除的过程。搞懂最小堆的相应知识后,最大堆与此类似。
- 最小堆示例:
【二】最小堆的操作
最小堆的构建:
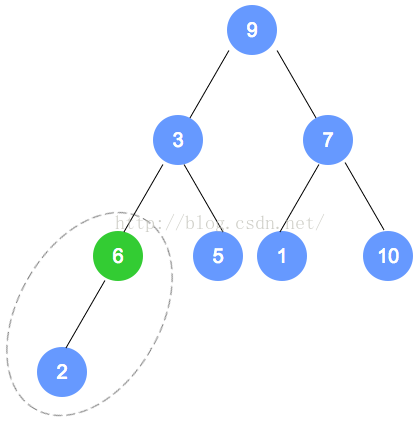
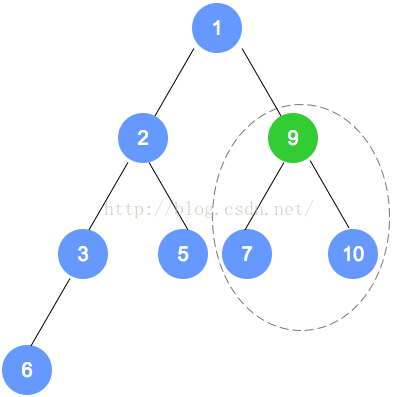
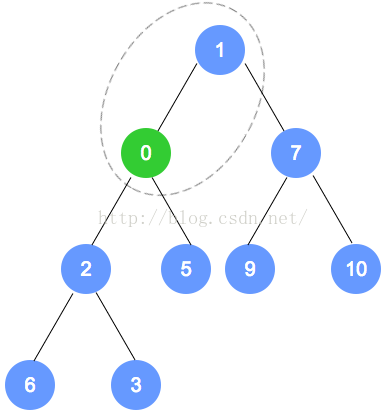
初始数组为:9,3,7,6,5,1,10,2
按照完全二叉树,将数字依次填入。
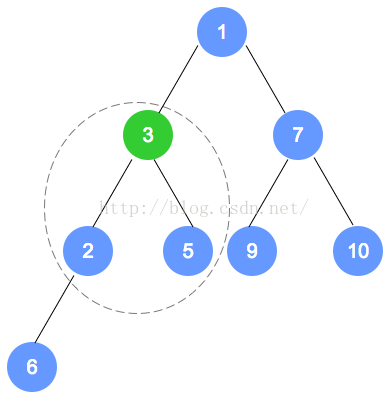
填入完成后,从最后一个非叶子结点(本示例为数字6的节点)开始调整。
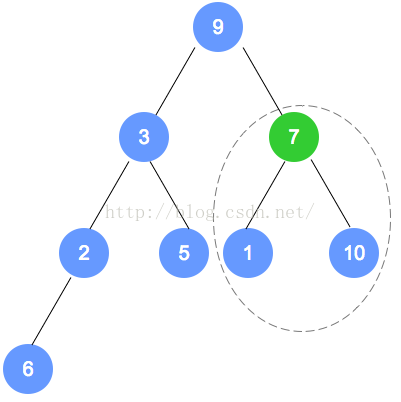
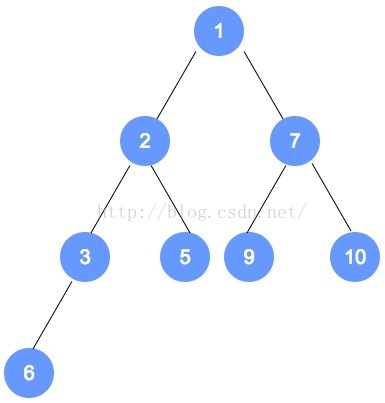
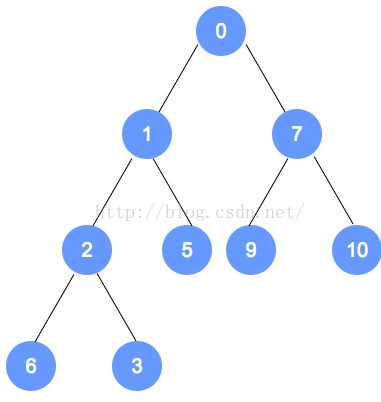
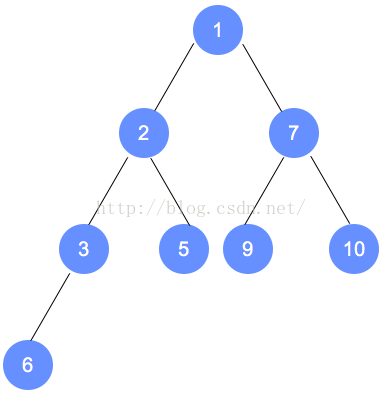
根据性质,小的数字往上移动;至此,第1次调整完成。
注意,被调整的节点,还有子节点的情况,需要递归进行调整。
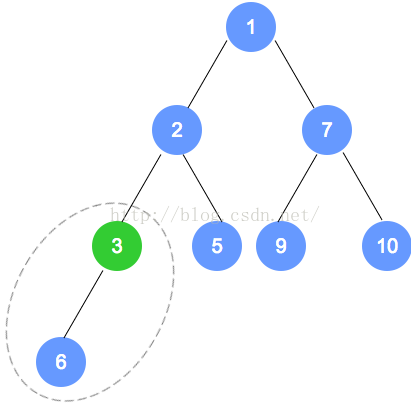
第二次调整,是数字6的节点数组下标小1的节点(比数字6的下标小1的节点是数字7的节点),
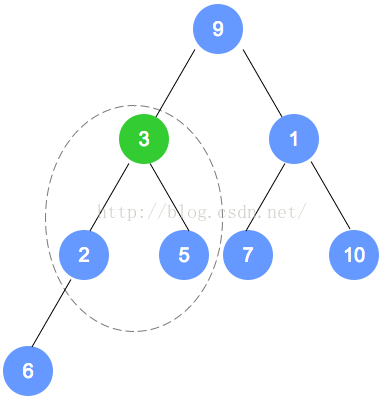
以下是本示例的图解:
注意:数字9的节点 将和 数字1的节点 发生对调,对调后,需要递归进行调整,请一定注意。
- 最小堆的元素插入 【插入到该二叉树的最后一个节点,再调整】
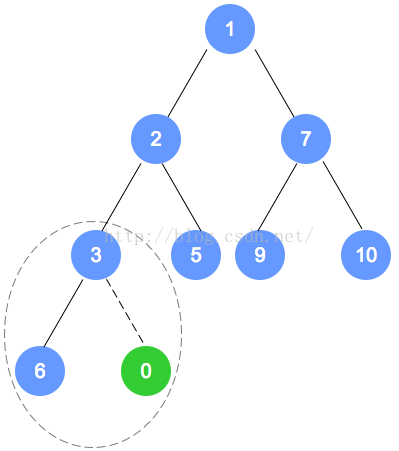
以上个最小堆为例,插入数字0。
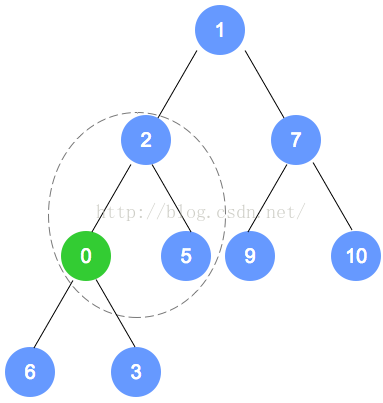
数字0的节点首先加入到该二叉树最后的一个节点,依据最小堆的定义,自底向上,递归调整。
以下是插入操作的图解:
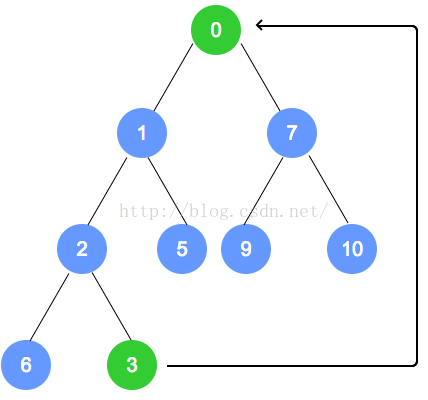
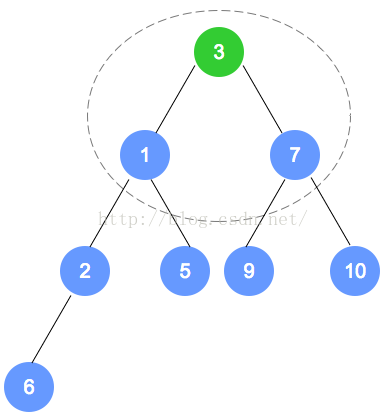
- 最小堆的节点删除【是把根节点删除,最后一个叶子节点放到根节点上,再调整】
对于最小堆和最大堆而言,删除是针对于根节点而言。
对于删除操作,将二叉树的最后一个节点替换到根节点,然后自顶向下,递归调整。
以下是图解:
【三】有一类常见的面试问题:
如何从一个存有10亿个数字的文档中获取到最大的10个数,计算机内存只有1M?
考虑10亿个数据很多,一次性无法装到我们的计算内存中,
采用常用的排序算法,可能也是不好进行操作,数据量很大,
这个地方可以想到可以才用小顶堆来解决这个问题。
1、让计算机去io读取文件
2、把读取出来的数据去构建一个包含10个元素的小顶堆
3、构建完成后,每次从文件中读取出来的一个数字和堆顶的元素进行比较,
如果比堆顶元素小,就直接丢弃或者跳过。如果读取出来的数据比堆顶元素大,
那么就可以用这个元素替代堆顶元素,进行调整小顶堆。这个算法的时间复杂度是O((100亿-1000)log(1000)),即O((N-M)logM),空间复杂度是M
转自:https://blog.csdn.net/wenge1477/article/details/101797674
这篇关于数据结构 小顶堆建堆过程 构建过程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!