本文主要是介绍大顶堆、小顶堆及其建堆过程、堆排序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
定义
按照堆的特点可以把堆分为大顶堆和小顶堆。
大顶堆:每个结点的值都大于或等于其左右孩子结点的值;
小顶堆:每个结点的值都小于或等于其左右孩子结点的值。
(堆的这种特性非常的有用,堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素)
我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
实现思路
堆是一种非线性结构,堆可以使用数组来实现,把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲,堆其实就是利用完全二叉树的结构来维护一个数组,但堆并不一定是完全二叉树。
不管是对堆进行插入、删除操作,还是使用堆排序,都少不了建堆的步骤。
堆排序
堆排序的基本思想:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
eg.
步骤1 建堆
构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
假设给定无序序列结构如下,

此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
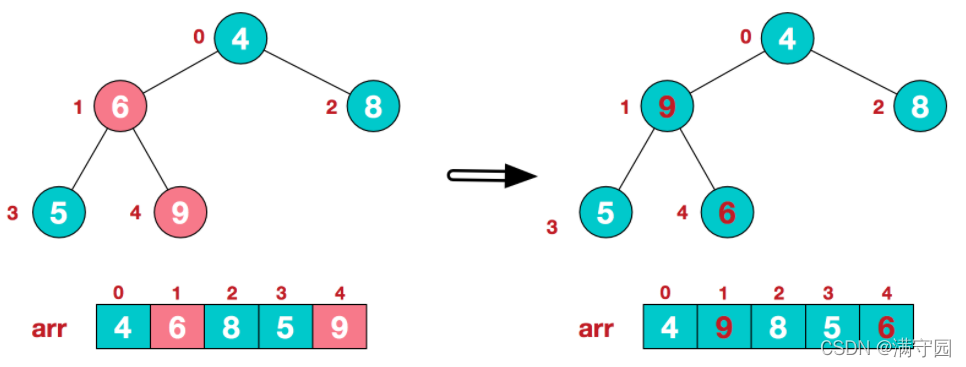
找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。

这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。

此时,我们就将一个无需序列构造成了一个大顶堆。
步骤2 堆顶和末尾置换,调整堆
将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
将堆顶元素9和末尾元素4进行交换
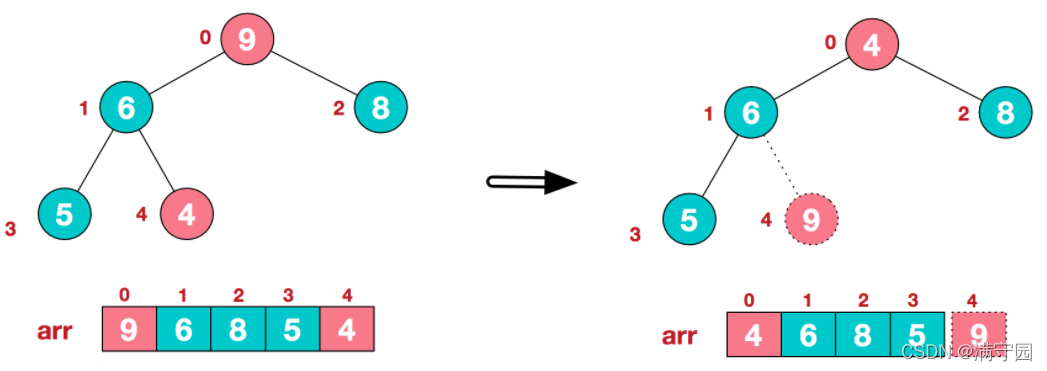
重新调整结构,使其继续满足堆定义
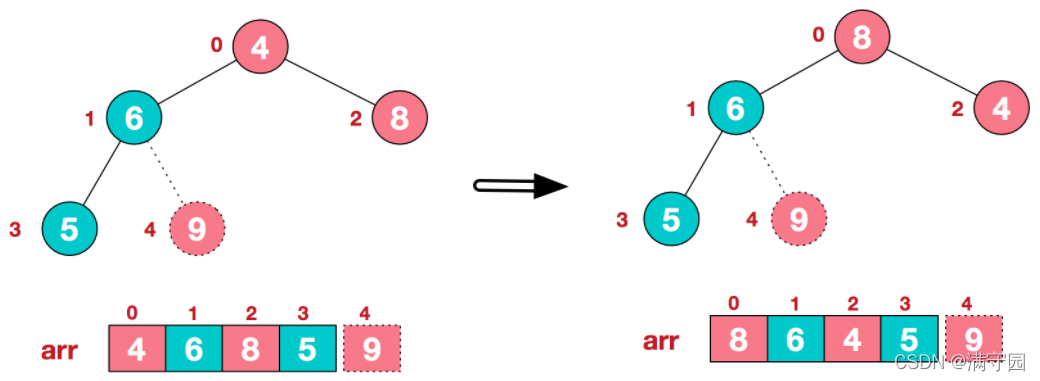
再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
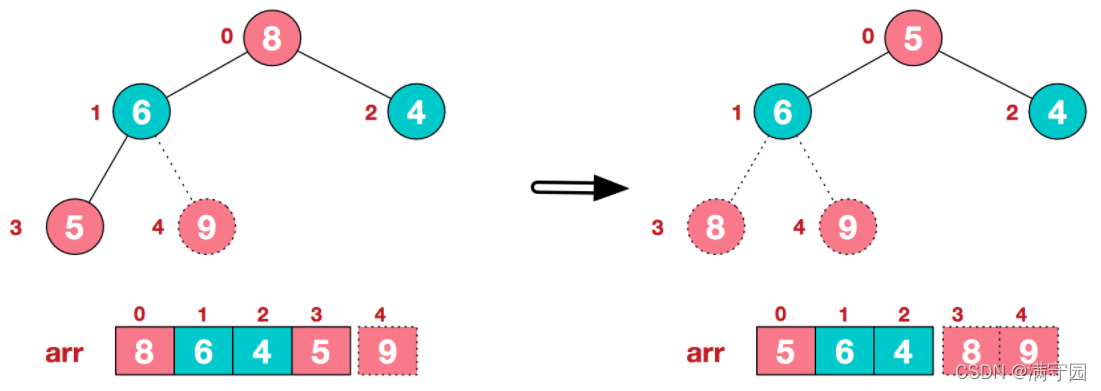
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

简单总结下堆排序的基本思路:
1. 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
2. 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3. 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
小顶堆代码实现如下,
#include<iostream>
using namespace std;void swap(int* a, int i, int m){int temp = a[i];a[i] = a[m];a[m] = temp;
}void heapify(int* a, int k, int index){int min = index;while(true){if(index*2+1<k && a[index*2+1] < a[index]){min = index*2+1;}if(index*2+2<k && a[index*2+2] < a[min]){min = index*2+2;}if(min == index)break;swap(a, index, min);//从交换后的节点开始继续往下堆化index = min;}
}void buildHeap(int* nums, int k){for(int i=k/2-1; i>=0; i--){heapify(nums, k, i);}
}void heapsort(int* nums, int k) {buildHeap(nums, k);for (int i = k - 1; i > 0; i--) {swap(nums, 0, i);heapify(nums, i, 0);}
}int main() {int nums[6] = {4, 2, 8, 5, 3, 2};heapsort(nums, 6);for (int i = 0; i < 6; i++) {cout << nums[i] << endl;}system("pause");return 0;
}大顶堆代码实现如下,
void heapify(int* a, int k, int index){int min = index;while(true){if(index*2+1<k && a[index*2+1] > a[index]){min = index*2+1;}if(index*2+2<k && a[index*2+2] > a[min]){min = index*2+2;}if(min == index)break;swap(a, index, min);//从交换后的节点开始继续往下堆化index = min;}
}换一种思路实现大顶堆,
#include<iostream>
using namespace std;void swap(int* a, int i, int m){int temp = a[i];a[i] = a[m];a[m] = temp;
}void heapify(int* a, int k, int index){int temp = a[index]; //index指向根节点 for(int j = 2*index+1; j<k; j = 2*j+1) { //从左孩子开始遍历temp = a[index];if(j+1 < k && a[j] < a[j+1]) { //比较左孩子和右孩子,将j指向较大的值j++;}if(temp < a[j]) { //如果根结点比孩子节点小,则交换,并将index指向该节点swap(a, index, j);index = j;} else {break; //反之,如果根节点比左右孩子都大,则结束遍历}}
}void buildHeap(int* nums, int k){for(int i=k/2-1; i>=0; i--){heapify(nums, k, i);}
}void heapsort(int* nums, int k) {buildHeap(nums, k);for (int i = k - 1; i > 0; i--) {swap(nums, 0, i);heapify(nums, i, 0);}
}int main() {int nums[6] = {4, 2, 8, 5, 3, 2};heapsort(nums, 6);for (int i = 0; i < 6; i++) {cout << nums[i] << endl;}system("pause");return 0;
}参考:
图解排序算法(三)之堆排序 - dreamcatcher-cx - 博客园
堆排序(大顶堆、小顶堆)----C语言 - 蓝海人 - 博客园
leetcode 215. 数组中的第K个最大元素【小顶堆】_ervy的博客-CSDN博客
大顶堆和小顶堆以及堆排_程序媛的梦工厂-CSDN博客
【算法】堆,最大堆(大顶堆)及最小堆(小顶堆)的实现_一名普通码农的菜地-CSDN博客_最小堆算法
谈谈堆排序,大顶堆,小顶堆? - 简书
Go 大顶堆 小顶堆 Heap使用方法_t949500898的博客-CSDN博客
这篇关于大顶堆、小顶堆及其建堆过程、堆排序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








