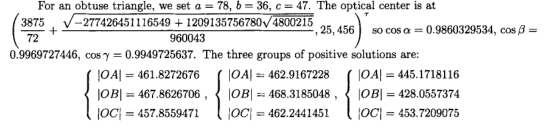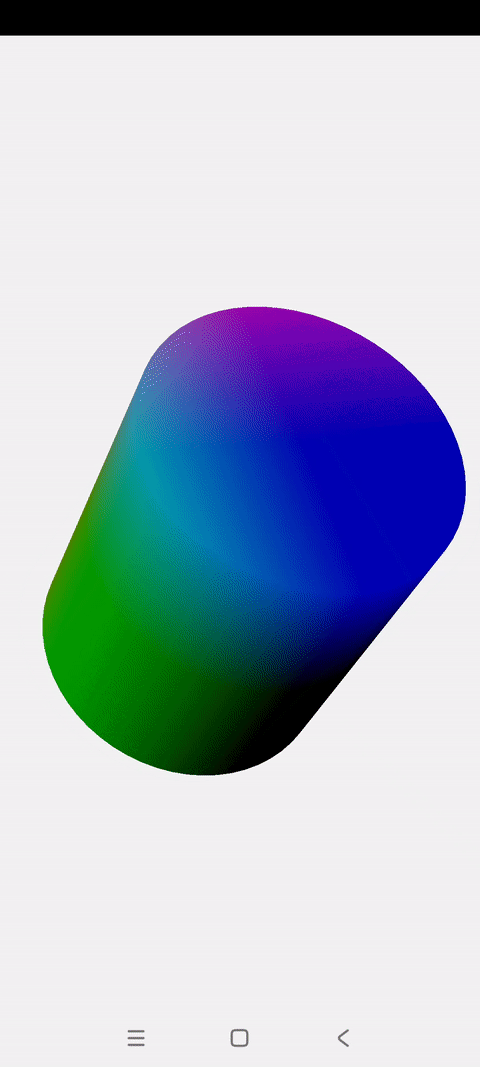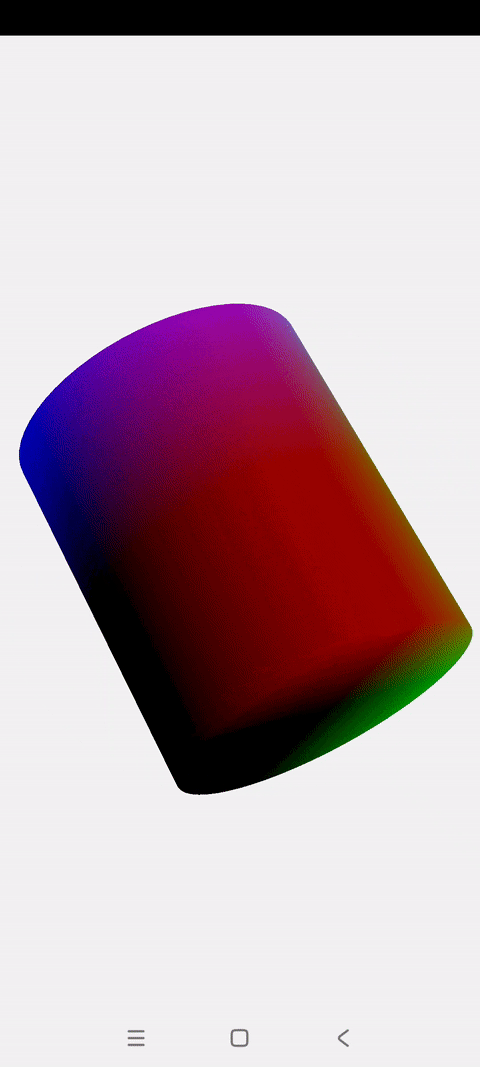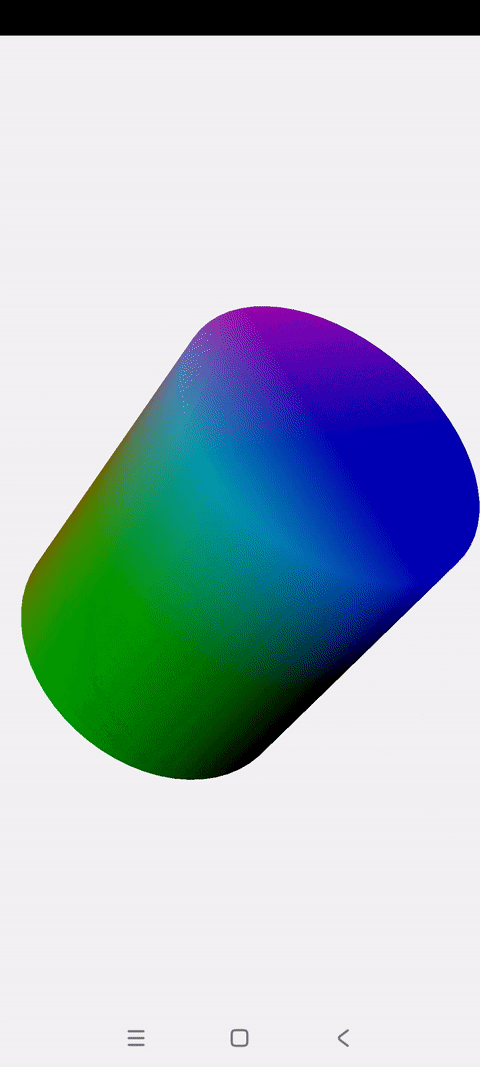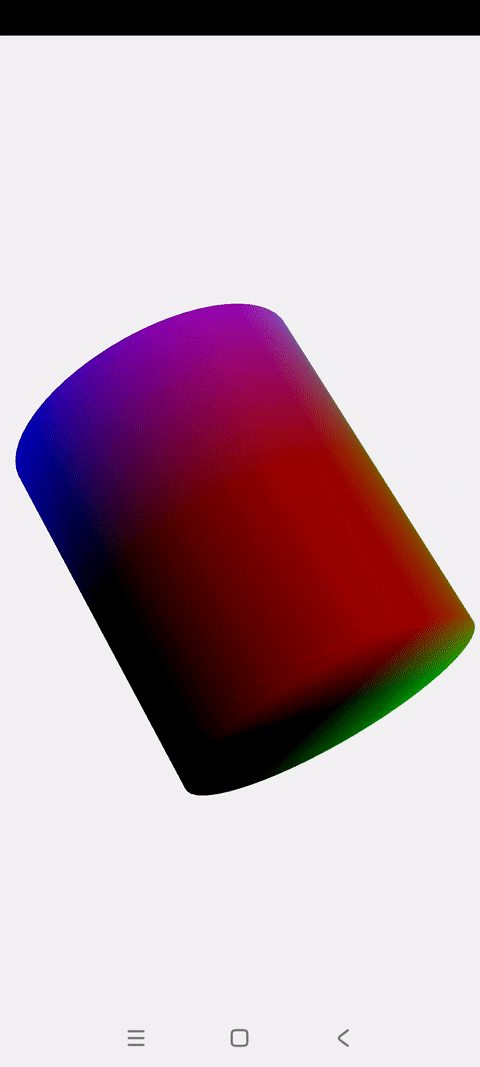圆柱专题
在 vue2 中实现 echarts 立体方形柱状图及立体圆柱
1、在做大屏项目时,为了页面不显得单调,有时设计会设计些立体的柱状图,前几天做大屏刚好遇到,记录一下。echarts本身没有配置直接配置立体图,立体图实质是三个图形合并堆积形成的视觉效果,分别是上面的盖,中间主体和下面的底,再配合中间主体的渐变颜色而实现。本文默认都是使用过echarts的,常规项不赘述,只看option的配置项,先上效果。 2、立体方块图 pdChartOptio
内六角圆柱头螺丝产品应用指南
内六角圆柱头螺丝是一种常见的紧固件,因其头部形状为圆柱形且顶部有一内六角孔而得名。这种螺丝广泛应用于机械制造、家具组装、电子产品等领域。下面我们将详细介绍内六角圆柱头螺丝的产品特点及应用指南。 一、产品特点 头部设计:圆柱形头部设计,外观简洁美观,易于隐藏。 内六角孔:头部中心的内六角孔方便使用内六角扳手或螺丝刀进行安装拆卸。 高强度:通常采用高强度钢材制成,能够承受较
拉普拉斯算子从笛卡尔坐标系到圆柱坐标系下的推导过程
这段时间推导圆膜振动方程的时候,需要将振动方程从笛卡尔坐标系转换到圆柱坐标系。虽然这个结果书上都有了,但是不满足于直接给出的结果,想自己推导一下。于是就有了下面的内容。总结起来:就是将笛卡尔坐标系下的拉普拉斯算子定义式和圆柱坐标系下拉普拉斯算子定义式之间的关系通过坐标转换对应起来,然后利用待定系数法求解相应的系数就可以了。话不多说,上干货。 笛卡尔坐标系下的拉普拉斯算子定义为: (2-1)
基于运动控制卡的圆柱坐标机械臂设计
1 方案简介 介绍一种基于运动控制卡制作一款scara圆柱坐标的机械臂设计方案,该方案控制器用运动控制卡制作一台三轴机械臂,用于自动抓取和放料操作。 2 组成部分 该机械臂的组成部分有研华运动控制卡,触摸屏,三轴圆柱坐标的平面运动机械结构,控制电柜包括伺服电机,上位机控制软件等部分组成。 3 控制方法
PCL 点到圆柱的距离(3D)
文章目录 一、简介二、实现代码三、实现效果参考资料 一、简介 这里的思路也很简单,我们只需要将点转换到圆柱坐标系下,在该系统中,点(0,0,0)为圆柱轴原点,(0,0,1)为圆柱轴方向,那么此时计算点到圆柱的距离就简单很多了,我们可以利用正射投影快速的获得距离结果。 二、实现代码 Cylinder3.h #pragma once#include "Line.h"
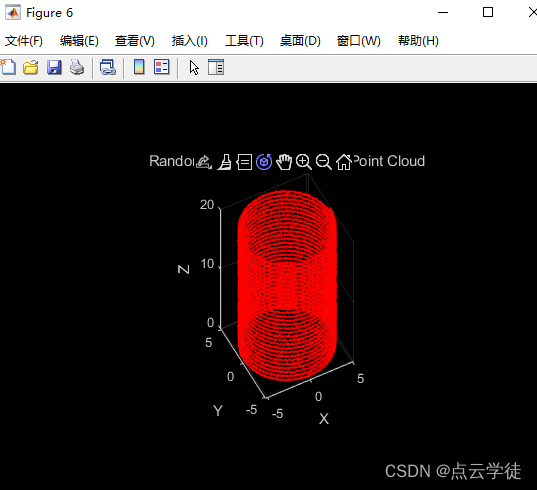
MATLAB 自定义生成圆柱点云(49)
MATLAB 自定义生成圆柱点云(49) 一、算法介绍二、具体实现1.代码2.效果 一、算法介绍 按照一些提前指定的圆柱参数,自定义生成圆柱点云,可添加噪声,用于后续的实验测试 二、具体实现 1.代码 代码如下(示例): % 指定圆柱的参数radius = 5; % 圆柱半径height = 20;
C++实践参考:点-圆-圆柱类族的设计
【项目 - 点-圆-圆柱类族的设计】 按以下的提示,由基类的设计和测试开始,逐渐地完成各个类的设计,求出圆格柱体的表面积、体积并输出并且完成要求的计算任务: (1)先建立一个Point(点)类,包含数据成员x,y(坐标点),实现需要的成员函数,并设计main函数完成测试; (2)以Point为基类,派生出一个Circle(圆)类,增加数据成员r(半径),以及求面积的成员函数area,实现其他
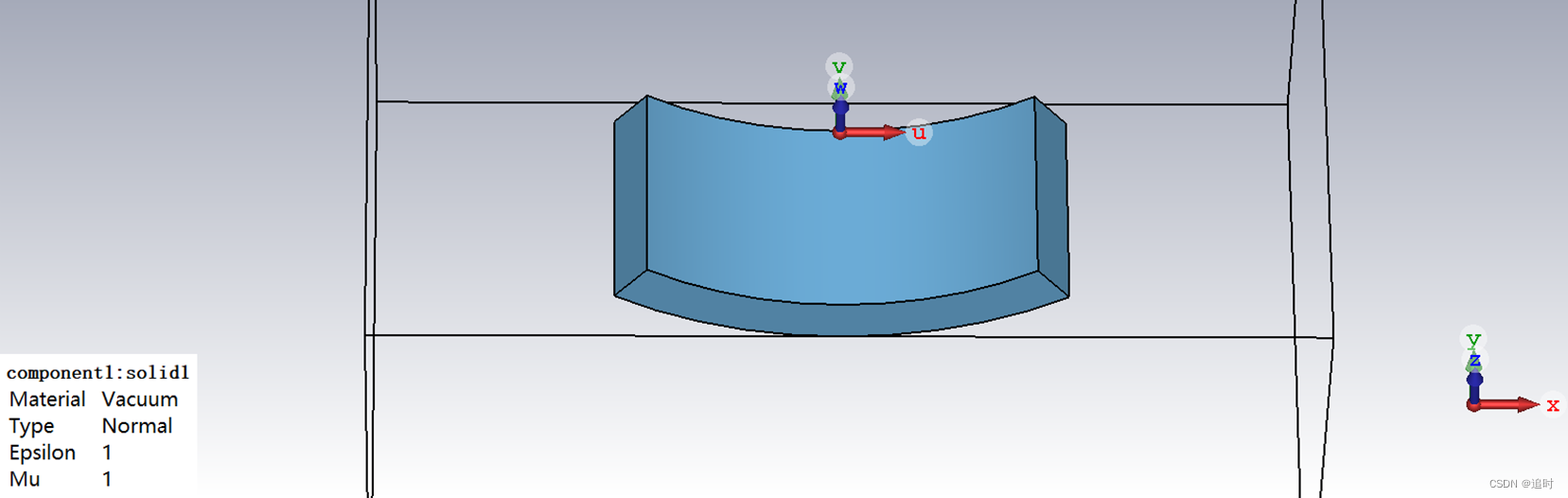
CST2018学习笔记:七、模型的圆柱弯折
1.建立立方体模型,将坐标系移动到立方体上表面的宽边。 2.选中立方体模型>Bend Tools>Cylindrical Bend,调出圆柱弯折的设置界面。 3.单向圆柱弯折:One sland>设置弯折角度Angle,完成模型的单向弯折。 4.双向圆柱弯折:Two sland>设置弯折角度Angle,完成模型的双向弯折。
【C++PCL】点云处理最小二成圆柱拟合
作者:迅卓科技 简介:本人从事过多项点云项目,并且负责的项目均已得到好评! 公众号:迅卓科技,一个可以让您可以学习点云的好地方 目录 1.原理介绍 2.代码效果 3.源码展示 4.参数调试 5.注意事项
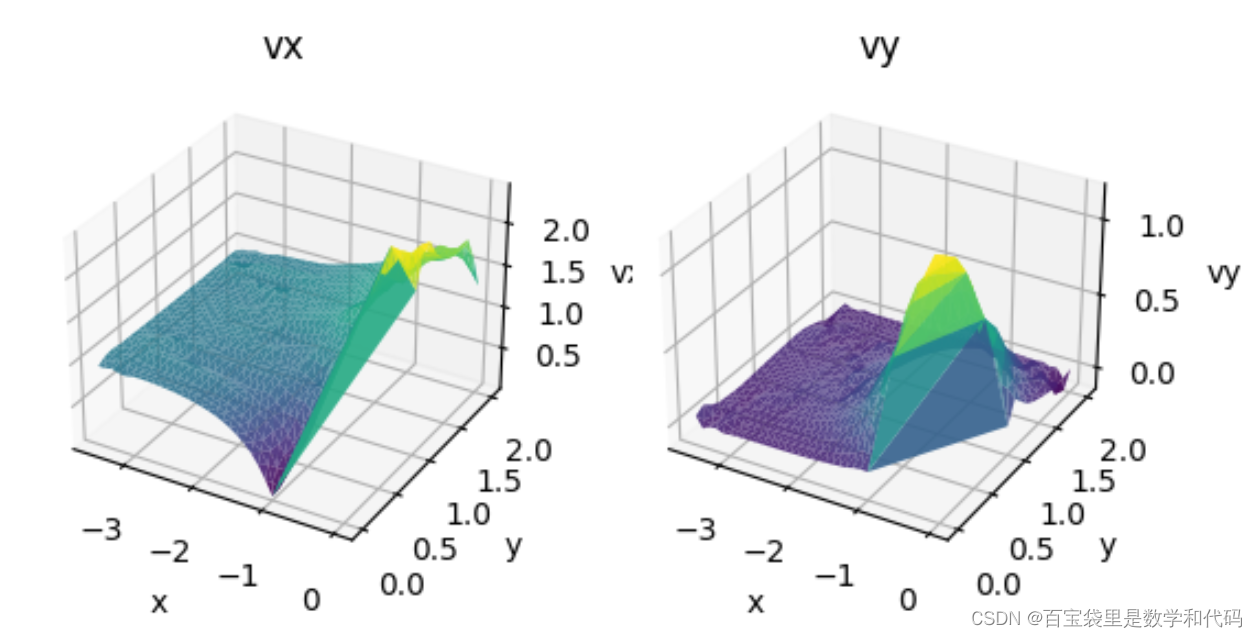
有限元法计算二维圆柱绕流问题——Python代码实现
一、问题描述 选取流函数Ψ为变量,对拉普拉斯方程进行求解(右边界为自然边界条件,其余边界为本质边界条件); 网格数据文件的生成暂时不在本文中详述。 二、节点和单元的数据读取 import numpy as npimport matplotlib as pltfrom mpl_toolkits.mplot3d import Axes3D# 打开文件try:with open('gr
PCL点云处理之自定义生成多种类型的圆柱点云(C++)(二百二十五)
PCL点云处理之自定义生成多种类型的圆柱点云(C++)(二百二十五) 一、算法介绍1.空心圆柱点云2.实心圆柱点云 二、算法实现1.生成方法1(空心)2.生成方法2(实心) 一、算法介绍 根据自己指定的圆柱长度、圆柱半径、以及中心轴的方向,生成一个圆柱点云数据,保存在PCD文件中。可以在后续的相关实验中使用。主要生成以下两种类型的圆柱点云: 1.空心圆柱点云 2.实心
几何题-求圆柱最大体积
点击打开链接 总是把问题看的太复杂,还以为是三分查找。这题根本没这个必要。 只要使圆周刚好与边相等就行了,矩形中最大的圆就是取最小边作为直径就行了。再分别以两边为高,比较就行了。水啊! 代码: #include<stdio.h>#include<math.h>#include<algorithm>using namespace std;const double pi=acos(
Matlab 画出不同位置高度的圆柱--样例二
1.所有圆柱的坐标、高和半径都是随机的,在此列出代码和样例: 2.初始化函数: define_yuanzhu.m function [xx,yy,zz,rr]=define_yuanzhu(k,xx,yy,zz,rr)%k为圆柱个数for j=1:kxx(j,1)=10.*randsample(20,1);yy(j,1)=10.*randsample(20,1);zz(j,1)=2.*ra
Matlab 画出不同位置高度的圆柱--样例
样例二是更加随机的情况,可见于博主的文章:matlab代码 画出不同位置高度的圆柱--样例二 圆柱信息: 圆心(1,1)高 1 圆心(3,1)高 2 圆心(4,3)高 3 clccloseclear%圆柱上表面自变量[a,r]=ndgrid((0:.05:1)*2*pi,[0 1]);xt=cos(a).*r;%21x2维yt=sin(a).*r;%21x2维%定义圆心xx
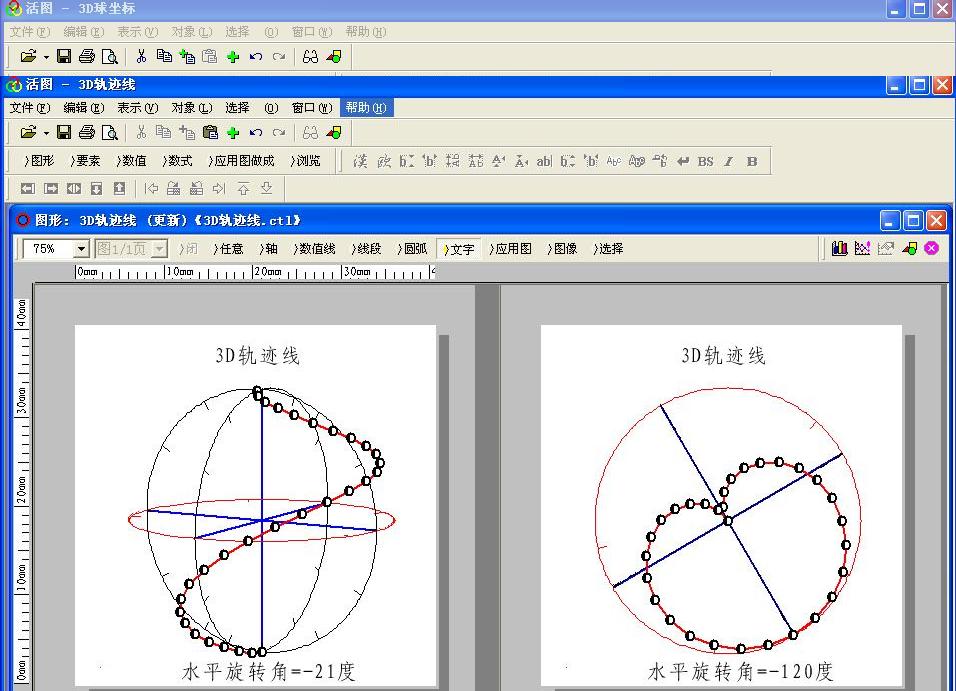
三维圆柱坐标和球坐标
在三维坐标系中,除了直角坐标系外,较常见用的较多的就是圆柱坐标和球坐标了。实际使用中,多半是用三维的图形表现来增强表现的渲染力﹑立体感和真实感,一般都是靠旋转三个角度(垂直轴旋转角﹑水平轴旋转角和画面轴旋转角),利用不同角度下的投影坐标值,在二维平面上表现出来的。由于实际物体的不规则化,有时即使是一个很简单的东西,用三维计算机图形来表现也会很复杂的,因为要对每一个点进行投影计算。好在现在的工具软件
Flash 特效原理:图片圆柱墙
网上也有这种不错的图片圆柱的效果,它有一些交互做得不错,采用cs4 或者3d引擎可以创造出这种图片圆柱墙的效果。这种效果主要涉及到圆的分布,借用这种圆的轨迹,我们可以实现这种圆柱图片墙的效果。是不是说错了?我们讨论的圆柱 而为什么提及到圆?那是因为圆这种数学模型在flash 当中是非要实现而基础的应用技术,从图片中看起来会像圆柱形状,但是实际上,我们只是重复复制两个圆,而他的高度只是不同
【论文翻译】危险圆柱为什么是危险的
为什么危险圆柱是危险的 摘要1 介绍2 初步措施2.1 基于距离的定义2.2 基于转换的定义2.3 这两个定义的等价性2.4 主要限制 3 主要结果主张证明 4 模拟备注 5 结论 摘要 PnP问题是计算机视觉界广泛使用的姿态确定技术,找出多个解决方案的几何条件是多解决方案分析的最终目的,也是解决该问题的关键问题。 本文证明,在给定3个控制点的情况下,如果摄像机的光学中心
OpenGLES:绘制一个混色旋转的3D圆柱
效果展示 本篇博文会实现两种混色效果的3D圆柱: 一.圆柱体解析 上一篇博文讲解了怎么绘制一个混色旋转的立方体 这一篇讲解怎么绘制一个混色旋转的圆柱 圆柱的顶点创建主要基于2D圆进行扩展,与立方体没有相似之处 圆柱绘制的关键点就是将圆柱拆解成:两个Z坐标不为0的圆 + 一个长方形的圆柱面 绘制2D圆的过程这里不再复述,不理解的可以参看前面这篇博文:《OpenGLES:绘制一个颜
碎片化学习Java(五)-- Java计算圆柱体积
本文参考 嗨客网 Java 实战 关键词: Java变量运算案例 Java计算圆柱体积案例 Java计算圆柱体积 题目 答案 原文 若要查看详细 解题思路、解题步骤、运行结果 原文链接:https://haicoder.net/case/java/java-variable-operator.html 后续 大纲:碎片化学习Java大纲 上一章:碎片化学习Jav
OpenGLES:绘制一个混色旋转的3D圆柱
效果展示 本篇博文会实现两种混色效果的3D圆柱: 一.圆柱体解析 上一篇博文讲解了怎么绘制一个混色旋转的立方体 这一篇讲解怎么绘制一个混色旋转的圆柱 圆柱的顶点创建主要基于2D圆进行扩展,与立方体没有相似之处 圆柱绘制的关键点就是将圆柱拆解成:两个Z坐标不为0的圆 + 一个长方形的圆柱面 绘制2D圆的过程这里不再复述,不理解的可以参看前面这篇博文:《OpenGLES:绘制一个颜
OpenGLES:绘制一个混色旋转的3D圆柱
一.概述 上一篇博文讲解了怎么绘制一个混色旋转的立方体 这一篇讲解怎么绘制一个混色旋转的圆柱 圆柱的顶点创建主要基于2D圆进行扩展,与立方体没有相似之处 圆柱绘制的关键点就是将圆柱拆解成:两个Z坐标不为0的圆 + 一个长方形的圆柱面 绘制2D圆的过程这里不再复述,不理解的可以参看前面这篇博文:《OpenGLES:绘制一个颜色渐变的圆》 废话不多说,正文开始了。 二.Render:
OpenGLES:绘制一个彩色、旋转的3D圆柱
一.概述 上一篇博文讲解了怎么绘制一个彩色旋转的立方体 这一篇讲解怎么绘制一个彩色旋转的圆柱 圆柱的顶点创建主要基于2D圆进行扩展,与立方体没有相似之处 圆柱绘制的关键点就是将圆柱拆解成:两个Z坐标不为0的圆 + 一个长方形的圆柱面 绘制2D圆的过程这里不再复述,不理解的可以参看前面这篇博文:《OpenGLES:绘制一个颜色渐变的圆》 废话不多说,正文开始了。 二.Render: