【论文翻译】危险圆柱为什么是危险的

摘要

PnP问题是计算机视觉界广泛使用的姿态确定技术，找出多个解决方案的几何条件是多解决方案分析的最终目的，也是解决该问题的关键问题。 本文证明，在给定3个控制点的情况下，如果摄像机的光学中心位于所谓的“危险圆柱”上，并且距控制点的支撑平面足够远，则相应的P3P问题必须有3个正解 。这个结果可以为更好地理解多解决方案问题带来一些新的见解。例如，在文献中显示，如果光学中心位于该危险圆柱体上，则P3P问题的解决方案是不稳定的，我们认为这种情况会发生。 三重解是这种不稳定的主要原因。

1 介绍

透视图n点问题，或简称为PnP问题，是计算机视觉，摄影测量甚至数学中的经典问题。 它最初是由Fishler和Bolles于1981年正式提出的，后来又被其他人广泛研究，例如[1-11]列举了一些。 仅当“ n”（即从空间控制点到其投影图像的点对应数）属于{3，4，5}或P3P问题，P4P问题和“ n”时，PnP问题才有意义。 P5P问题。 这是因为，当n <3时，问题没有得到很好的定义，而当n> 5时，例如可以通过直接线性变换方法来线性解决问题。
在P3P问题，P4P问题和P5P问题中，最基本的一个是P3P问题，因为它的广泛适用性以及它在其他两个问题中扮演的关键角色。在文献中，已经对P3P问题进行了广泛的研究。 Su等。表明P3P问题具有无限多个解的充要条件是其三个控制点与相机中心的共圆性。Fishler和Bolles表明P3P问题最多具有4个正解，并且这个上界也是可实现的
Haralick等人。回顾和比较了解决P3P问题的不同直接方法。给出了P3P问题的完整解决方案分类。他们的结果纯粹是代数的，在实际应用中似乎没有如最初所述直接求解4阶多项式那样的指导性。因此，有必要对P3P问题的多个解进行几何解释。在[13]中，获得了P3P问题具有4个解的一般条件。本文为P3P问题提供了充分的条件。有3个解决方案。
尽管P3P问题已在文献中进行了广泛研究，但我们认为本研究值得报道：首先，这些结果可以为更好地理解多解决方案问题带来一些新见解。例如，它在[14]中显示。如果光学中心位于危险圆柱体上，P3P问题的解决方案是不稳定的，我们认为这种三重解决方案的出现是造成这种不稳定性的主要原因。其次，结果纯属几何，可以用作理论指导。实际应用中，通过适当安排控制点来避免有害的多重解决方案问题。
在本文中，粗体大写字母表示矩阵或非均匀3向量，粗体小写字母表示图像点的均匀3向量，T代表转置，| * | 表示实数的绝对值，|| * || 表示向量或矩阵的Frobenius范数。

2 初步措施

为了清楚和方便起见，本节将首先列出P3P问题的两种定义，继承关系和基本约束。 它们是我们得出主要结论的必要要素，将在第3节中进行详细说明。

2.1 基于距离的定义

定义为：给定3个控制点的相对空间位置，并给距视点中心的每对控制点一个角度，确定各个控制点距视点中心的距离。
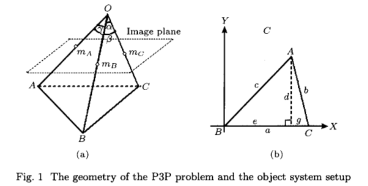
如图1（a）所示，根据余弦定律，A，B和C是三个控制点，O是光学中心。我们有以下熟悉的约束系统：

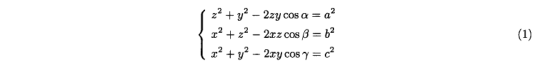
其中a = IBCI，b = IACI，c = |ABI。z= IOAI，Y = IOBI，z = IOCI是在基于距离的定义下要确定的三个距离。

2.2 基于转换的定义

定义如下：给定3个具有已知坐标的控制点在一个以对象为中心的帧中，以及它们在图像平面上的相应投影，并在给定相机固有参数的情况下，找到对象帧与相机Dame之间的转换矩阵[3]。
如图1（b）所示，A，B和C是三个控制点，它们的非均匀坐标分别是MA，MB和Me。为简化此问题，设置了一个特殊的对象框架，使

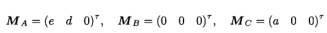
其中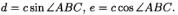
在不失一般性的情况下，让内在相机参数矩阵成为恒等矩阵，并且在均质坐标中分别对应的三个对应图像点分别是mA，mB，mc，它们都是单位矢量，即||mA|| = 1，||mB|| = 1，||mC|| = 1 ；那么透视成像过程可以表示为：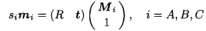
其中sA，sB，sC是三个未知比例因子，R,t是3X3旋转矩阵和平移向量，因此，我们具有以下约束：

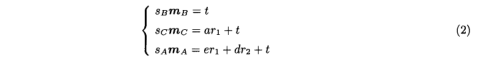
在（2）中，R =（r1，r2，r1xr2），t是在基于变换的定义下确定的变换参数。

2.3 这两个定义的等价性

首先，我们证明在（1）和（2）中x = sA，y = sB，z = sC。这是因为根据投影理论[15,P.144]，如果O是光学中心，则

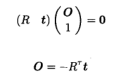
然后

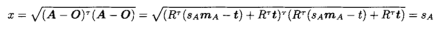
类似的，y = sB，z = sC。
接下来，我们证明这两个定义是相等的。这是很明显的，因为从（2）知道，如果知道r1,r2,t，就可以唯一确定sA，sB，sC。相反，如果知道了sA，sB，sC 因此，本文中，两个定义将被区分开使用。

2.4 主要限制

约束（2）可以进一步简化为：

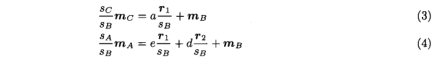
令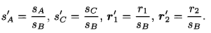
从（3）可得到

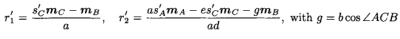
通过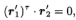
我们有第一个主约束方程

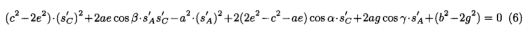
其中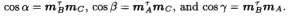
这两个约束等式是第3节中提出的主要结果证明的基础，其中sA和sC是要确定的两个未知数。
在结束本节之前，应先讨论另一点，即如何从s’A和s’C导出sA，sB，sC。可按以下步骤进行。
首先，根据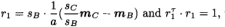
我们有

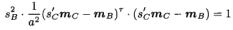
接着有

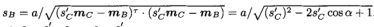
并且sC,sA由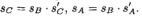
显然，不同的集合（s’A，s’c）必须导致不同的集合（sA，sB，sC），因此在下一节中，我们将显示在（5）和（6）中的条件下，s’A和s’C 可以有3个正解。 为了符号上的方便，在下一部分中，将（5）和（6）中的s’A，s’C分别表示为sA和sC。

3 主要结果

危险圆柱体定义为外接控制点A，B，C，其控制轴垂直于平面A，B，C[14]（参见图2）。在[14]中，基于约束雅可比矩阵奇异性分析， 结论是，如果光学中心位于危险圆柱体上，则相应的P3P的解就不稳定。在这项工作中，我们证明这种不稳定性可能主要来自多种解。

主张

如图2所示，A，B，C是三个控制点，如果光学中心O位于除少数几条直线上的危险圆柱体上，并且从O到平面A，B，C的距离足够大，则对应的P3P问题{0,(A,B,C)}必须有3个正解。

图2（a）当光学中心O处于危险圆柱体上时，对应的P3P问题必须具有3个正解。（b）3个正解的示例：{O,ABC}，{O,A’8’C’），{O,A” B” C”}

在给出上述结果的形式证明之前，请先概述。证明由以下两个主要步骤组成：首先将（5）和（6）中两个变量（sA，sC）的两个二次约束方程式转换为4次单变量多项式，然后将该多项式 被分解成一个单变量方程和两个相同的线性方程。其次，单变量方程具有两个正根。

证明

步骤1.当光学中心位于危险圆柱体上时，可以将（5）和（6）中的约束分解为一元二次方程和两个相同的线性方程。
如图2（a）所示，P是光学中心O在ABC平面上的投影，更确切地说，在三角形ABC的外接圆上，线AM穿过圆心AN⊥BC，并且 M，N在圆上。
假设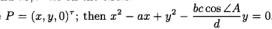
即，P位于外接圆上。
令|OP| = h;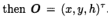


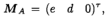
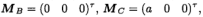
有

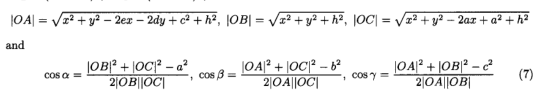
1）当cosβsC-cosγ = 0时
通过一些简单的计算，我们可以证明，当cosβsC-cosγ= 0时，P必须与点A，B或N一致。可以证明：
1.1）如果P与A一致，则（5）和（6）必须有三个正解；
1.2）如果P与M或N一致，但b≠c，则（5）和（6）仍具有三个正解；
1.3）如果P与M或N重合，但b = c，则M和N将重合，因此（5）和（6）只有两个正解。
由于上述三种情况是孤立的，可以通过简单地将相关条件代入（5）和（6）来证明，因此将省略详细步骤。
2)当cosβsC-cosγ ≠ 0时
通过（5），可以得到

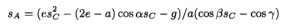
将sA代入（6）有

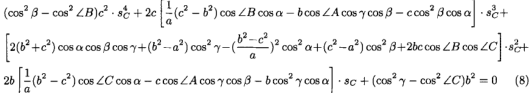
将(7)代入(8),即，当光学中心限于危险圆柱体时，可以将（8）分解为

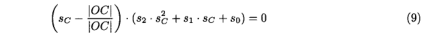
其中


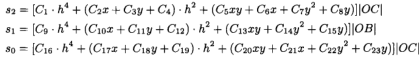
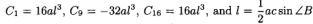
由(9)我们得到

步骤2 从（10）和（11）中得到三种不同的正解。
步骤2.1除个别情况外，（10）中的Sc不是（11）的根。当sC = | OC | / | OB |时，我们有sA = | OA | / | OB |。这是一组正解 P3P问题。
另外，有必要显示在什么条件下SC = | OC | ／ | OB | 不是（11）的根。在（11）的左侧替换sC = | OC | ／ | OB | ，我们有

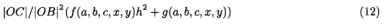
其中 f(a,b,c,x,y) 和 g(a,b,c,x,y) 都是{a,b,c,x,y} 的函数。因此，如果 f(a,b,c,x,y) 和 g(a,b,c,x,y) 不同时等于0，则（12）不能等于0，即sC = |OC|／|OB|也不能是(11)的根。以下是 f(a,b,c,x,y) 和 g(a,b,c,x,y) 同时等于0时所有可能情况的枚举 。



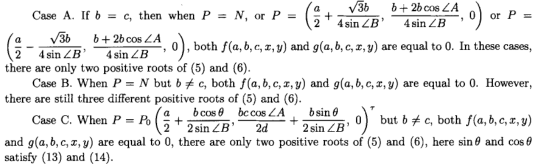
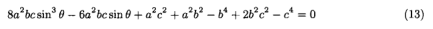
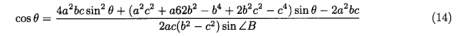
总而言之，如果在案例A，案例B和案例C中P不是上述要点之一，则sC = |OC|／|OB|不能为（ii）的根。
步骤2.2 （11）具有两个不同的正根
首先，如果光学中心距离平面ABC足够远，则s2，s1和s0的符号将与系数C1，C9和C16的符号相同。 因此s2> 0，s1 <0，s0> 0。
此外，（11）的判别式为

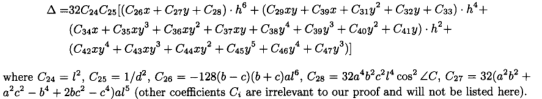
用△δ表示h6的系数。

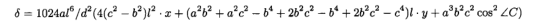
当h大时，以△> 0为序，则δ> 0。下面将证明。
因为光学中心在平面ABC上的投影P =（z，Y，0）T满足圆方程，所以x可以表示为变量y的函数，因此，δ也可以表示为a
显然，δ（y）是连续且可微的，因此δ（y）在以下闭合区间内可达到其最大值和最小值：

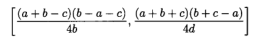
在其一阶导数为0或在区间的两个端点处。
δ相对于y的一阶导数用δy’表示，二阶导数用δy’'表示。因为（z，y）在圆上：

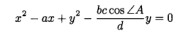
当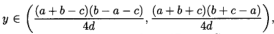
，通过一些简单的计算，我们可以证明
当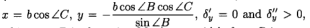
因此δ达到最小值0
但是，在这种情况下，P是点M。按照之前的推论，假设P与点M，N不同，我们可以得出结论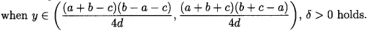

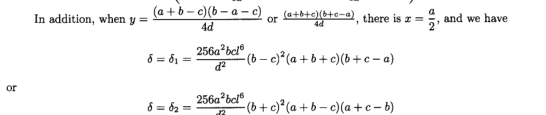
显然，总是保持δ2> 0。但是，对于5δ，如果b≠c，δ1> 0；如果b = c，δ1= 0。但是正如我们之前所说，当b = c时，P与M点重合，并且 因此，在我们的假设中不包括这种情况。因此，在这两个端点处，δ> 0也成立。
结合这两种情况，我们知道当Y在封闭区间内时，δ> 0成立，即，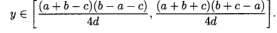

显然，L1≠0且b≠c，L2≠0。这表明在这种情况下，sC = 1并非（11）的根。然而，当b = c时，L2 = 0，但是在最后一种情况下，P2与点M重合， 它不包括在我们的假设中。
结合情况1和情况2，sC = 1并不是（11）的根，即sC≠1成立，则λ12> 0成立。因此，如果光学中心距控制点平面足够远，则PA> 0，因此 sA> 0。
因此，我们可以得出结论，当光学中心位于危险圆柱体上，除了上面的几条线之外，并且放置在距控制点平面足够远的位置时，相应的P3P问题必须具有三个正解。
在此阶段，我们可以对命题中无效的“几行”给出明确的规范。实际上，这些行是在步骤2中的案例A和案例C中定义的。

4 模拟

所有的仿真都由Maple7执行。仿真步骤如下：首先，随机选择三个控制点A，B，C形成三角形，然后像图2一样构造其危险圆柱体，并在危险圆柱体上任意选择一个点作为光学中心，然后计算三个侧面a。 ，， b，c和三个角α，β，γ，最后将a，b，c和α，β，γ代入（1）中的方程，并求解。为方便起见，我们建立了一个坐标框架，使X 轴与AC重合，Y正轴穿过B，

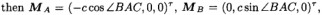
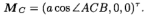由于空间限制，我们将仅针对钝角三角形报告一个示例。
对于钝角三角形，设a = 78，b = 36，c = 47。光学中心在

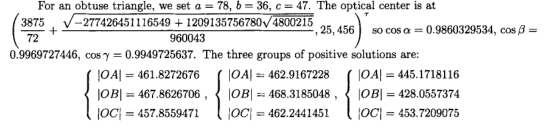
备注

1）本文表明，如果光学中心距离控制点的支撑平面足够远，则相应的P3P问题必须具有3个正解。但是，现阶段尚无明确的“远方”规范，它取决于与三角形ABC有关的特定关系。从仿真中可以看出，距离不必太大。
2）表明，（11）△的判别式中h的最高度为6，而（11）的s1和s2中h的最高度为4，因此当光学中心距平面ABC足够远时，即h很大，则（11）将有两个非常接近的解（c．f．模拟中钝角三角形的例子）。这与[13]中的不稳定性解释相符。

5 结论

得出了一个P3P问题具有3个正解的一般充分条件。我们认为，当光学中心位于危险圆柱体上时，这种多重解的出现是观察到的不稳定性的主要来源[14]。我们的结果纯属几何且对于从业人员在实际应用中正确安排控制点很有帮助。