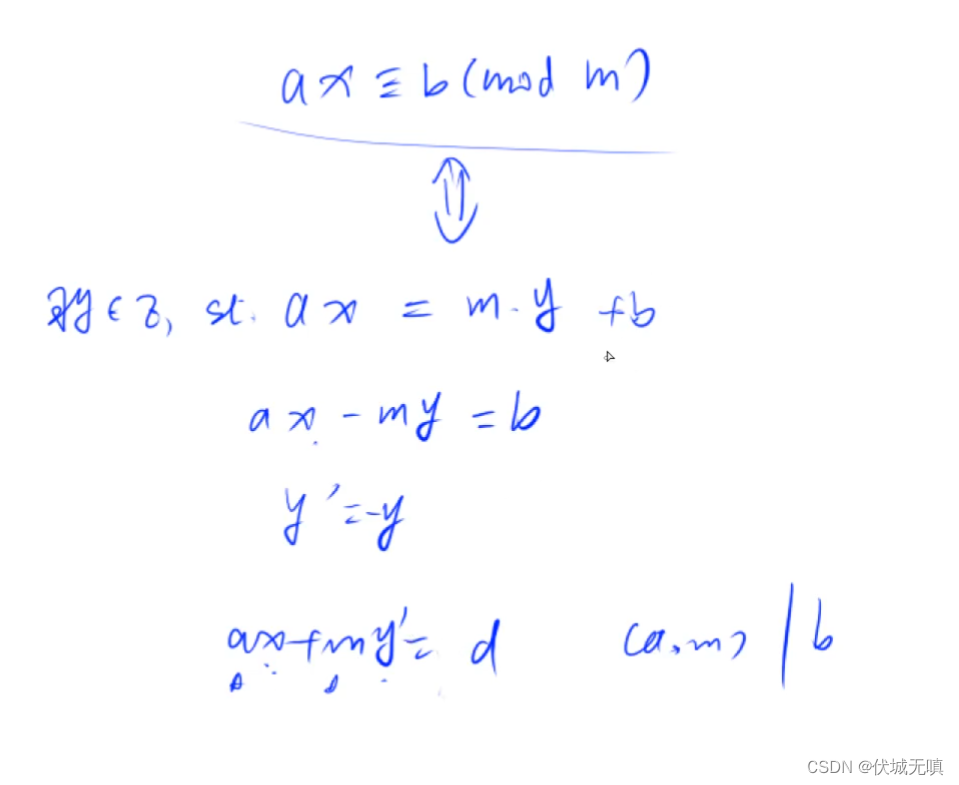同余专题
数论 - n元线性同余方程的解法
note:n元线性同余方程因其编程的特殊性,一般在acm中用的很少,这里只是出于兴趣学了一下 n元线性同余方程的概念: 形如:(a1*x1+a2*x2+....+an*xn)%m=b%m ..................(1) 当然也有很多变形,例如:a1*x1+a2*x2+...+an*xn+m*x(n+1)=b.这两个都是等价的。 判断是否有解:
POJ1006同余方程基础
题目链接:http://poj.org/problem?id=1006 问题描述 人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天。一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期。然后再给出一个起始日期,要求从这一天开始,算出最少再过
再说中国剩余定理、扩展欧几里德和同余方程组
E - 解同余线性方程组1 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status Description Andy和Mary养了很多猪。他们想要给猪安家。但是Andy没有足够的猪圈,很多猪只能够在一个猪圈安家。举个例子,假如有16头猪,An
再说中国剩余定理、扩展欧几里德与同余方程组
E - 解同余线性方程组1 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status Description Andy和Mary养了很多猪。他们想要给猪安家。但是Andy没有足够的猪圈,很多猪只能够在一个猪圈安家。举个例子,假如有16头猪,A
hdu 1573 X问题(线性同余方程)
X问题 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 3847 Accepted Submission(s): 1226 Problem Description 求在小于等于N的正整数中有多少个X满足:X
HDU2815 Mod Tree【高次同余方程】
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=2815 题目大意: 有一颗树,每个节点有K个儿子,那么问题来了:能否算出这棵树的最小深度D,使得这个深度 的节点数对P取模的结果为N吗? 思路: 转换一下题目含义,就变成了解K^i = N(mod P),典型的A^i = B(mod C)问题,此题B的范围 明显在[0,C-
POJ2417 Discrete Logging【高次同余方程】
题目链接: http://poj.org/problem?id=2417 题目大意: 已知整数P、B、N满足公式B^i = N(mod P),求i的值是多少。 思路: 典型的解高次同余方程A^x = B(mod C),直接套模板解决。注意输入顺序:C A B AC代码: #include<iostream>#include<algorithm>#inclu
POJ3243 Clever Y【高次同余方程】
题目链接: http://poj.org/problem?id=3243 题目大意: 已知公式A^x mod C= B,以及A、C、B的值,求解x的值为多少。 思路: 典型的求解方程A^x = B(mod C),直接模板解决。 AC代码: #include<iostream>#include<algorithm>#include<cstdio>#incl
HDU3579 Hello Kiki【一元线性同余方程组】
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=3579 题目大意: Kiki有X个硬币,她用不同的方式数了N次,每次她把硬币分成大小相等的组,记录每次一组硬币 的个数Mi和数完最后剩余的硬币数Ai。那么问题来了:总共有多少枚硬币? 思路: 典型的一元线性同余方程组X = Ai(mod Mi)求解。题目要求输出最小正整数解,
HDU1573 X问题【一元线性同余方程组】
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1573 题目大意: 求在小于等于N的正整数中有多少个X满足:X mod a[0] = b[0], X mod a[1] = b[1], X mod a[2] = b[2], …, X mod a[i] = b[i], … (0 < a[i] <= 10)。 思路: 先求出
HDU5478 Can you find it【同余问题】
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=5478 题目大意: 给你一个素数 C(1 <= C <= 2*10^5) 和整数 k1、b1、k2(1 <= k1,k2,b1 <= 10^9)。 找出有多少个(a,b)满足 a^(k1*n+b1) + b^(k2*n-k2+1) ≡ 0(mod C)(n = 1,2,3,…) 如果
随机数 -- 线性同余
#include<iostream> #include<iomanip> #include<stdlib.h> #include<math.h>using namespace std;const int sizes = 100;double random( int& temp ){int i;int result;static int x1,x2,x3;static int if
基础算法——前缀和和同余定理——K倍区间
题源:P8649 [蓝桥杯 2017 省 B] k 倍区间 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 一、预备知识(自行学习) 1、一维前缀和 2、同余定理 二、解题代码 f[x] --- 某个前缀和对k取余的结果是x的个数f[0]=1---取余是0那这个区间就是一个K倍区间,而其他的需要两个区间的差才能构成K倍区间先求res再求f[sum]的原因也是其他的需
网络空间安全数学基础·整除与同余
主要内容: 整除的基本概念(掌握) 素数(掌握) 同余的概念(掌握) 1.1整除 定义:设a,b是任意两个整数,其中b≠0,如果存在一个整数q,使 a = qb,则我们称b整除a,或a被b整除,记为b|a,此时称 b是a的因子,a是b的倍数。 例:a=10, b=2则有2|10;若a=100, b=10有10|100 例:设a是整数,a≠0, 则a|0。 整除的基本性质: 1. 如果
P1082 同余方程 扩展欧几里德算法 C++
题目描述 求关于x xx的同余方程 ax≡1(modb) a x \equiv 1 \pmod {b}ax≡1(modb) 的最小正整数解。 输入格式 一行,包含两个正整数 a,b,用一个空格隔开。 输出格式 一个正整数 x0,即最小正整数解。输入数据保证一定有解。 输入输出样例 输入 #1 3 10 输出 #1 7 说明/提示 【数据范围】 对于 40%的数据,2≤b≤1,00
ACM 数论 同余的性质
同余的性质 同余,顾名思义,就是许多的数被一个数d去除,有相同的余数。d数学上的称谓为模。如a=6,b=1,d=5,则我们说a和b是模d同余的。因为他们都有相同的余数1。 数学上的记法为: a≡ b(mod d) 可以看出当n<d的时候,所有的n都对d同商,比如时钟上的小时数,都小于12,所以小时数都是模12的同商. 对于同余有三种说法都是等价的,分别
poj1061 青蛙的约会(扩展欧几里得算法求解同余方程)
青蛙的约会 Description 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止。可是它们出发之前忘记了一件很重要的事情,既没有问清楚对方的特征,也没有约定见面的具体位置。不过青蛙们都是很乐观的,它们觉得只要一直朝着某个方向跳下去,总能碰到
算法——数论——同余
目录 同余 一、试题 算法训练 同余方程 同余 同余使人们能够用等式的形式简洁地描述整除关系同余:若 m(正整数),a 和 b 是整数,a%m==b%m,或(a-b)%m==0,记为 a b(mod m)求解一元线性同余方程等价于求解二元线性丢番图方程 一元线性同余方程 ,解法看下面第一题二元线性丢番图方程 逆:的一个解为 a 模 m 的逆 一、试题 算法训练 同余方
辗转相除法和同余原理
辗转相除法和同余原理 辗转相除法同余原理 辗转相除法 辗转相除法就是用来求出两个数的最大公约数的方法,那么这个方法怎么用呢?举个例子:有两个数,a=12,b=8,要求这两个数的最大公约数,首先让a%b得到4,然后让a=b,b=a%b,即现在a=8,b=4;继续用a%b得到0,然后让a=b,b=a%b,现在a=4,b=0。当b等于0的时候,a的值就是原来两个数的最大公约数
C++ 数论相关题目 线性同余方程 (扩展欧几里得算法的应用)
给定 n 组数据 ai,bi,mi ,对于每组数求出一个 xi ,使其满足 ai×xi≡bi(modmi) ,如果无解则输出 impossible。 输入格式 第一行包含整数 n 。 接下来 n 行,每行包含一组数据 ai,bi,mi 。 输出格式 输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi ,如果无解则输出 impossible。 每组数据结果占一行,结果可能不唯一,输
求解线性同余方程--扩展欧几里得
资料来源:https://blog.csdn.net/ //求解ax=b(mod m) 返回0为无解,否则返回gcd(a,m)个mod m意义下的解,用X[]存int mod(int a, int b, int m){return equation(a, m, b);} 先看一道题目:
【初等数论】同余方程、与二次剩余互反律
同余方程、二次剩余、二次互反律 1、同余方程 剩余类可以看做是一个新的数系,它对加减乘运算是封闭的,所以同余方程对多项式是有意义的。这里我们就来讨论下一元多项式方程(1)的解,当然它的解是一个剩余类集合,最多有 m 个解。 f ( x ) = ∑ k = 0 n a
leetcode 523. Continuous Subarray Sum | 523. 连续的子数组和(同余定理)
题目 https://leetcode.com/problems/continuous-subarray-sum/ 题解 没有想到 O(n) 的方法,于是直奔答案: 参考1:【宫水三叶】拓展到求方案数问题 参考2:证明+动图:帮你吃透本题 核心思想: 草稿: class Solution {public boolean checkSubarraySum(int[
算法基础之线性同余方程
线性同余方程 核心思想: 转化为扩展欧几里得 求得结果d 必须为 b的因数 #include<iostream>#include<algorithm>using namespace std;typedef long long LL;const int N = 100010;int exgcd(int a,int b,int &x,int &y){if(!b){x = 1 ,y = 0;