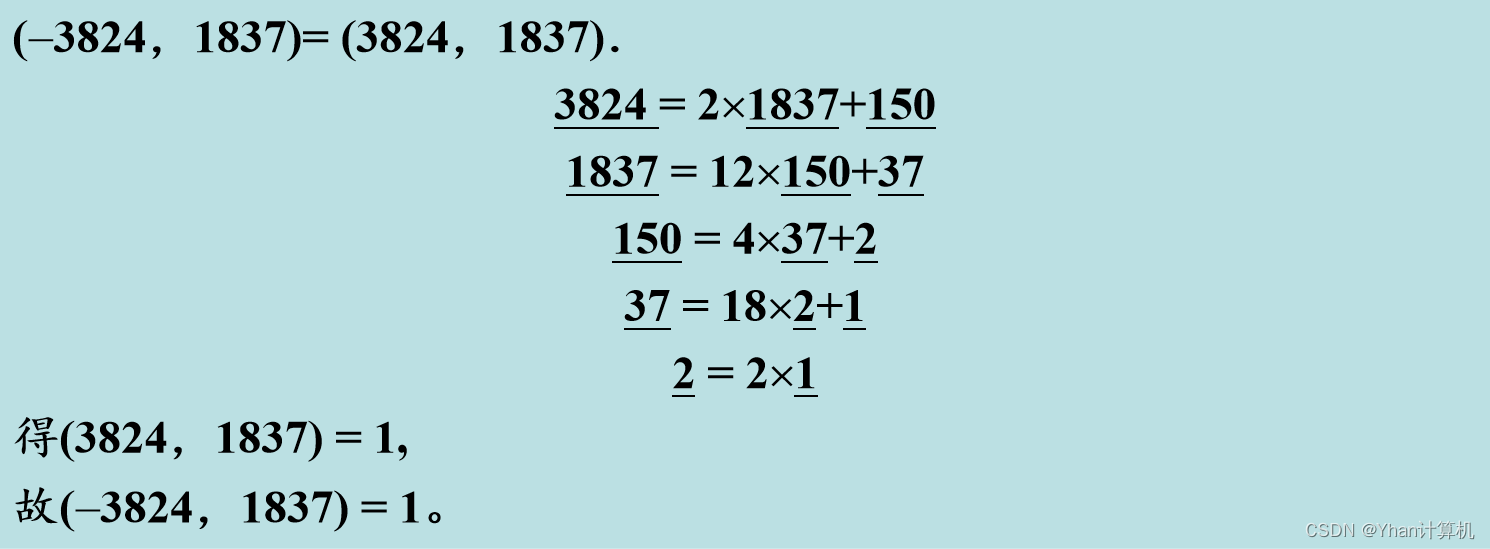本文主要是介绍网络空间安全数学基础·整除与同余，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
主要内容：
整除的基本概念（掌握）
素数（掌握）
同余的概念（掌握）
1.1整除
定义：设a，b是任意两个整数，其中b≠0，如果存在一个整数q，使 a = qb，则我们称b整除a，或a被b整除，记为b|a，此时称 b是a的因子，a是b的倍数。
例：a=10, b=2则有2|10；若a=100, b=10有10|100
例：设a是整数，a≠0, 则a|0。
整除的基本性质：
1. 如果b|a且a|b，则b = a或b = -a。
2. 如果a|b且b|c，则a|c。
3. 如果c|a且c|b，则c|ua+vb，其中u，v是整数。
整除的基本性质（补充）：
(1) a|b<=>-a|b<=>a|-b<=>-a|-b<=>|a| | |b|
(2) b≠0且a|b => |a|≤|b|
带余除法：当两个整数不能整除时，我们有带余除法：
定义：对于a，b两个整数，其中b≠0，则存在唯一q，r使得：a=bq+r，0 ≤ r<|b|。r称为a被b除得到的余数, 当r = 0时，b|a。
例：
1）a = –37， b= 5，则–37 = (-8)×5+3，q=8，r=3
2）a = 67，b= 7，则67=(9)×(7)+4，q=9， r=4
最大公因子：
定义：
1) 设a，b是两个整数，如果整数c|a且c|b，则c称为a，b的公因子。
2) 设c>0是两个不全为零的整数a，b的公因子，如果a，b的任何公因子都整除c，则c称为a，b的最大公因子，记为c=(a,b)。
最大公因子性质：
1.(a,b)=(-a,b)=(a,-b)=(-a,-b)=(|a|,|b|)
2.(0,a)=a
最大公因子（求解）
例：(-3824，1837)
最大公因子定理：
定理：设a，b是两个不全为零的整数，则存在两个整数u, v，使得：(a, b)=ua+vb。
例：将a = 888，b = 312的最大公因子表示为(a,b) = ua+vb。
1.2互素
定义：设a，b是两个不全为0的整数，如果(a, b)=1，则称a，b互素。
推论：a, b互素的充分必要条件是：存在u，v，使ua+vb=1。
互素性质：
1) 如果c|ab且(c, a) = 1，则c|b 。
2) 如果a|c，b|c，且(a, b) = 1，则ab|c 。
3) 如果(a,c) = 1，(b,c) = 1，则(ab,c) =1 。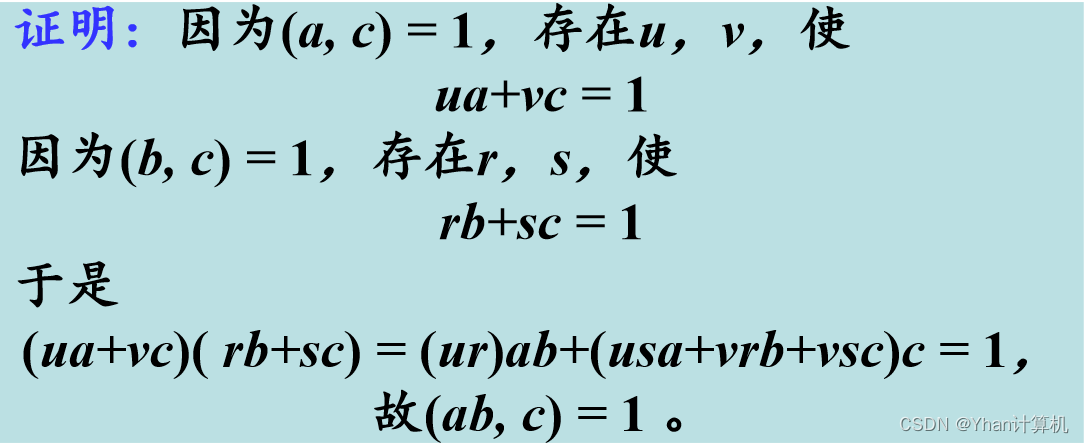
最小公倍数：
定义：
1) 设a, b是两个不等于零的整数．如果a|d，b|d，则称d是a和b的公倍数。
2) a和b的正公倍数中最小的称为a和b的最小公倍数，记为[a,b] 。
最小公倍数性质：
[a，b] = [–a，b] = [a，–b] = [–a，–b] = [|a|，|b|]
例：a = 2，b = 3．它们的公倍数集合为{0，±6，±12，±18，…}.而[2，3] = 6 。
最小公倍数与最大公因子关系：
定理：
1) 设d是a，b的任意公倍数，则[a, b] | d 。
2)
，特别地，如果(a, b) = 1, [a, b] = |ab|。
1.3素数
定义：如果一个大于1的整数p除±1和±p外无其他因子，则p称为一个素数，否则称为合数。
定理：设p是一个素数，则
1) 对任意整数a，如果p不整除a，则(p，a) = 1。
2) 如果p|ab，则p|a，或p|b。
算术基本定理：
定理：每个大于1的整数a都可以分解为有限个素数的乘积：a=p1p2…pr。该分解除素数因子的排列外是唯一的。
标准因子分解式：
由于p1，p2，…，pr中可能存在重复，所以a的分解式可表示为有限个素数的幂的乘积：
，这称为a的标准因子分解式。
例：2100的标准因子分解式：
素数无穷个：
定理：素数有无穷多个。
Eratosthenes筛法：
定理：设a是任意大于1的整数，则a的除1外最小正因子q是一素数，并且当a是一合数时，
。
对于一般N，Eratosthenes筛法可表述如下：
第1步 找出的全部
素数：p1，p2，…，pm。
第2步 在1~N中分别划去p1，p2，…，pm全部倍数。
第2步完成后剩下的数除1外就是不超过N的全部素数。
筛法原理如下：对于一个数a≤N，如果p1，p2，…，pm都不整除a，则a是素数。这是因为如果a是合数，则由定理它必有一素因子在p1，p2，…，pm中。
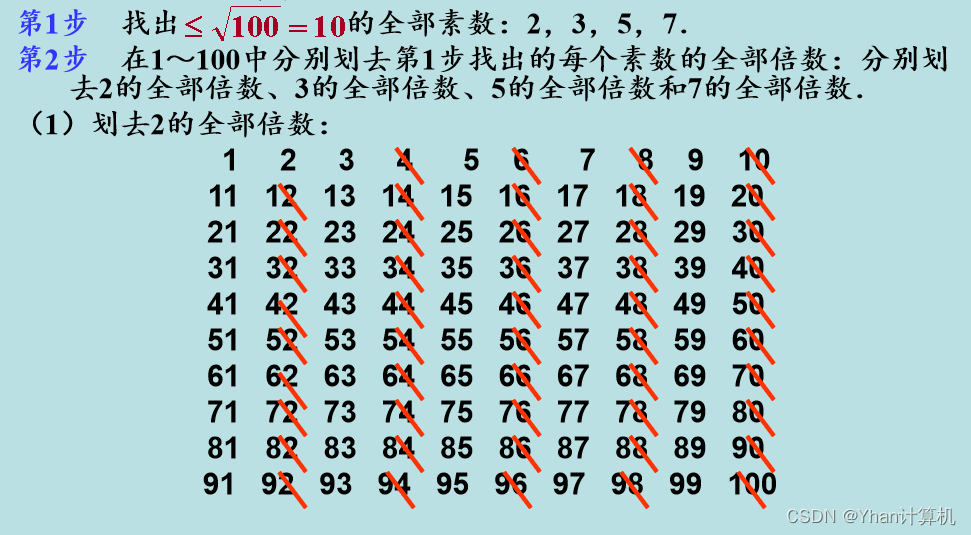
例：求不超过100的全部素数。
同理可以将因子5，7的倍数划去： (3) 划去5的全部倍数： (4) 划去7的全部倍数。
最终经过上述步骤后剩下的数除1外就是不超过100的全部素 数： (25个) 2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97
1.4 同余
定义：给定一个称为模的正整数m。如果m除整数a，b得相同的余数，即a=q1m+r，b=q2m+r，0≤ r小于等于m， 则称a和b关于模m同余，记为 a≡b (mod m)
例：25≡1(mod 8)，16≡-5(mod 7)。
定理：整数a，b对模m同余的充分必要条件是：m|(a-b)，即a = b+mt，t是整数。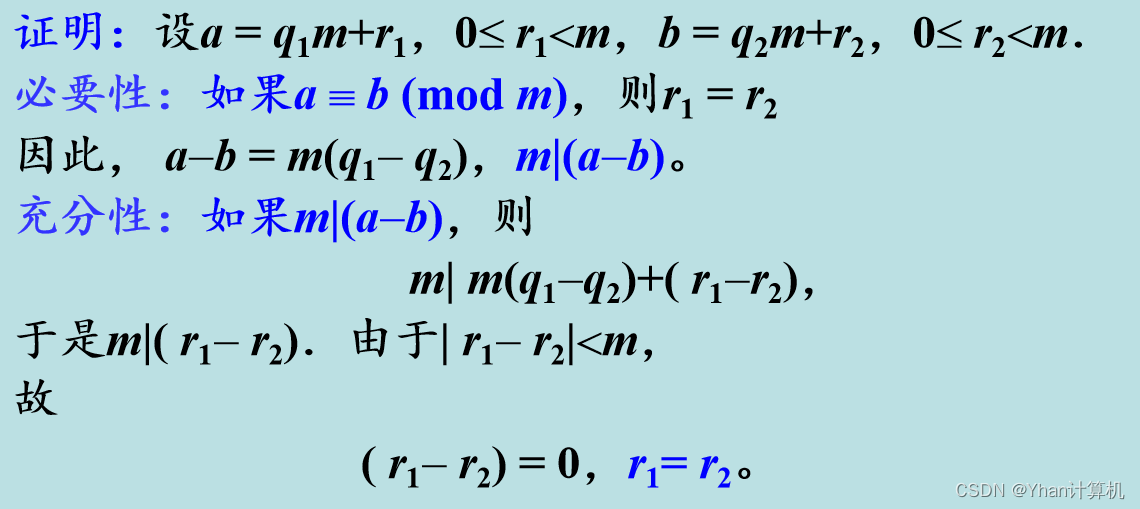
同余性质及推论：
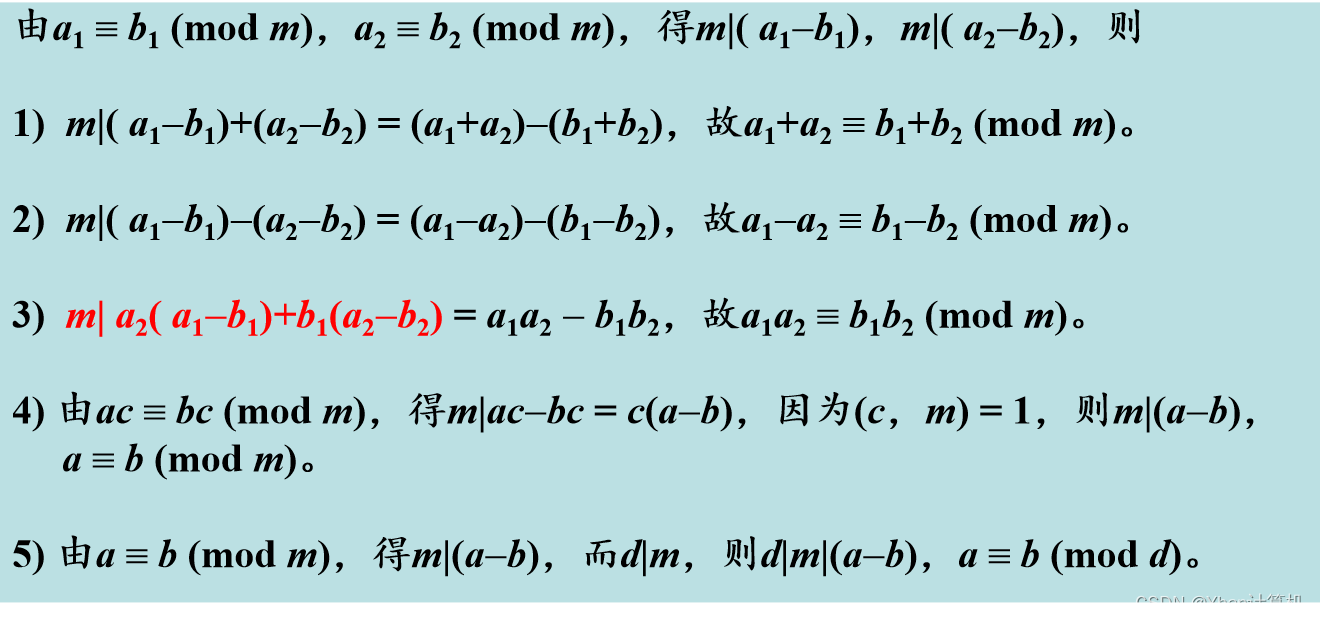
推论：如果a1≡b1 (mod m)，a2≡b2 (mod m)，则：
快速指数算法
例1-16：求解 2^64 (mod 641)
这篇关于网络空间安全数学基础·整除与同余的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
