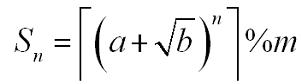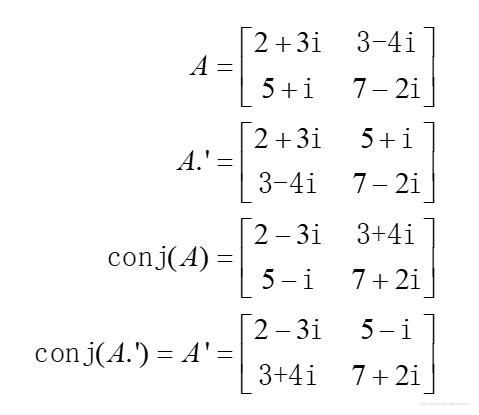共轭专题
数学基础 -- 线性代数之共轭转置矩阵
共轭转置矩阵 1. 共轭转置矩阵的定义 共轭转置矩阵(Hermitian transpose)是线性代数中的一个重要概念,特别是在处理复数矩阵时经常使用。它的定义包括两个步骤: 转置:将矩阵的行和列互换。共轭:对矩阵中的每个元素取复共轭,即将复数的虚部取负。 数学表达 对于一个 m × n m \times n m×n 的复矩阵 A A A ,其共轭转置矩阵 A † A^{\dag
【构造共轭函数+矩阵快速幂】HDU 4565 So Easy! (2013 长沙赛区邀请赛)
【题目链接】 :click here~~ 【题目大意】: A sequence Sn is defined as: Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate Sn. You, a top coder, say
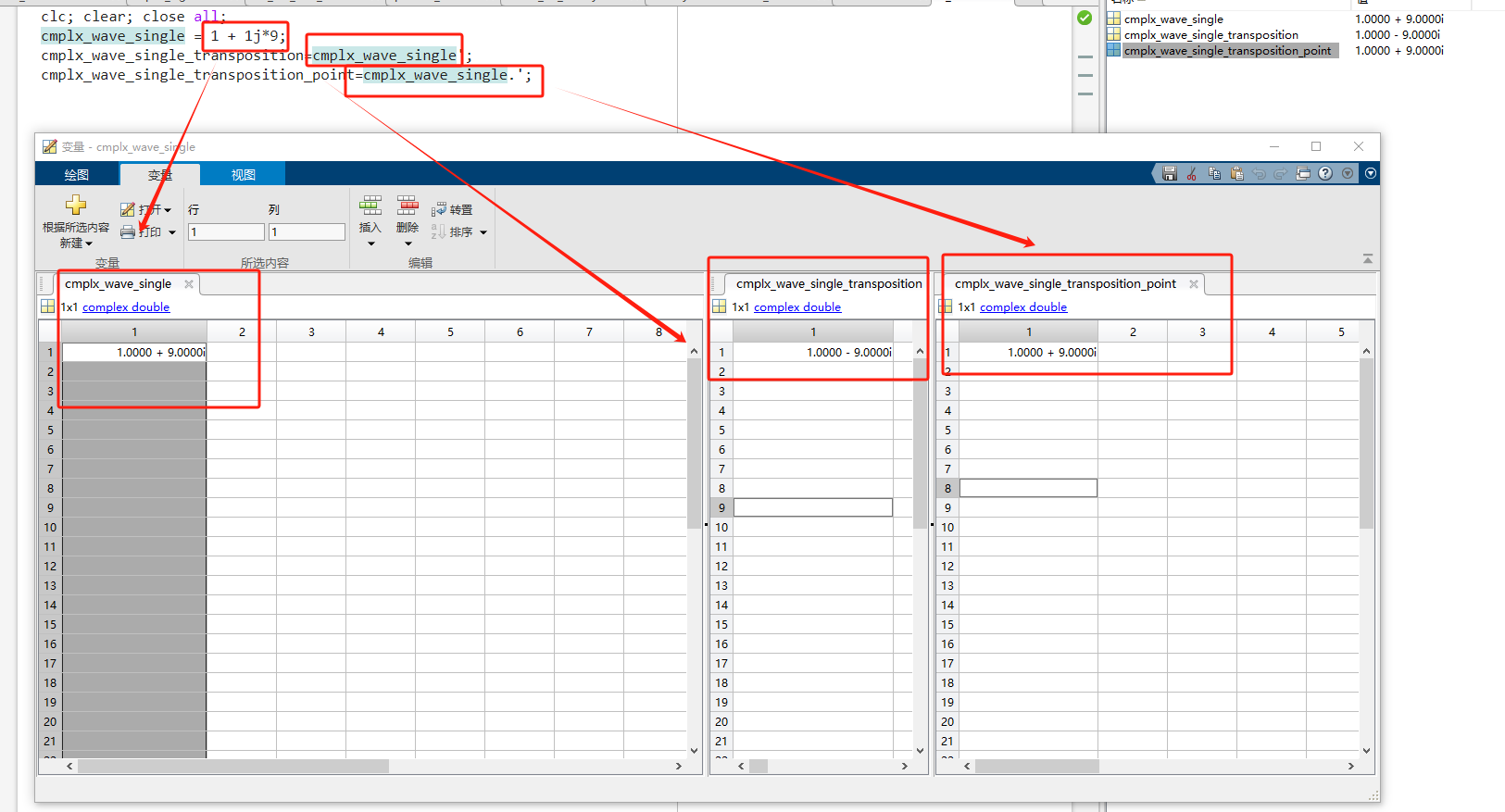
使用matlab的大坑,复数向量转置!!!!!变量区“转置变量“功能(共轭转置)、矩阵转置(默认也是共轭转置)、点转置
近期用verilog去做FFT相关的项目,需要用到matlab进行仿真然后和verilog出来的结果来做对比,然后计算误差。近期使用matlab犯了一个错误,极大的拖慢了项目进展,给我人都整emo了,因为怎么做仿真结果都不对,还好整体的代码都是我来写的,慢慢往下找就找到了问题的来源,全网没有看到多少人把这个愚蠢的错误写出来,我来引入一下。 代码错误的表现:复数向量的虚部被取反,正数变成负数,负数
PCG 梯度共轭(加权的DCT相位展开)相位解包裹 matlab 过程解析-加权最小二乘相位展开技术
1.代码 % check if the weight has the same size as psiif (~all(size(weight) == size(psi)))error('Argument error: Size of the weight must be the same as size of the wrapped phase');end%论文(公式 15)中的矢量 b
共轭先验-Conjugate Prior
定义:如果先验分布和似然函数可以使得先验分布和后验分布有相同的形式,那么就称先验分布与似然函数是共轭的。 读数理统计学导论时,遇到过共轭先验的概念。 贝叶斯判别准则中,分别假设了先验分布 p(θ) p(\theta),后验分布 p(θ|X) p(\theta|X),以及 p(X),p(X|θ) p(X), p(X|\theta)似然函数。 贝叶斯定理可以写作: P(θ|X)=P(θ)P(
PCG共轭梯度最小二乘相位解包裹-matlab(可直接运行)
phase_unwrap.m %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 根据Ghiglia和Romero(1994)提出的方法,基于加权和非加权最小二乘法进行相位解包裹% 链接:https://doi.org/10.1
共轭梯度法 Conjugate Gradient Method (线性及非线性)
1. 线性共轭梯度法 共轭梯度法(英语:Conjugate gradient method),是求解系数矩阵为对称正定矩阵的线性方程组的数值解的方法。 共轭梯度法是一个迭代方法,它适用于 1. 求解线性方程组, 2. 共轭梯度法也可以用于求解无约束的最优化问题。 我们想最小化目标函数f(x),假设其拥有二次形式: 最优化问题表示如下: 上式可以等价于求解线性方程组 Ax
PSMA-BCH特异性膜抗原(PSMA)通过肽合成器合成了NOTA共轭前体NOTA-PSMA
名称:PSMA-BCH 分子量:940.45 分子式:C45H64N8O14 纯度:95% 结构式: 陕西新研博美生物科技有限公司的特异性膜抗原(PSMA)是癌诊断重要靶点。通过肽合成器合成了NOTA共轭前体NOTA-PSMA(也称为PSMA-BCH),其化学纯度超过95%。68Ga PSMA BCH是通过用68GaCl3对NOTA-PSMA进行放射性标记获得的,68GaCl3的放射
预条件共轭梯度下降法PCG浅谈
简介 共轭梯度法是一种求解SPD系统线性方程组的迭代方法。它本来是一种直接法,但是通过迭代法求解后,配合复杂的预条件方法,反而更受欢迎。 我们将求解 转化为求解phi(x) 的最小值 注意:A的SPD性质确保了它的唯一性。 线性搜索法 将线性求解的问题转化为求最小值的问题后,我们尝试用线性求解的方式。我们首先选择一个初始位置,不同的方法会选择不同的方向和step lengt
人工智能之数学基础【共轭梯度法】
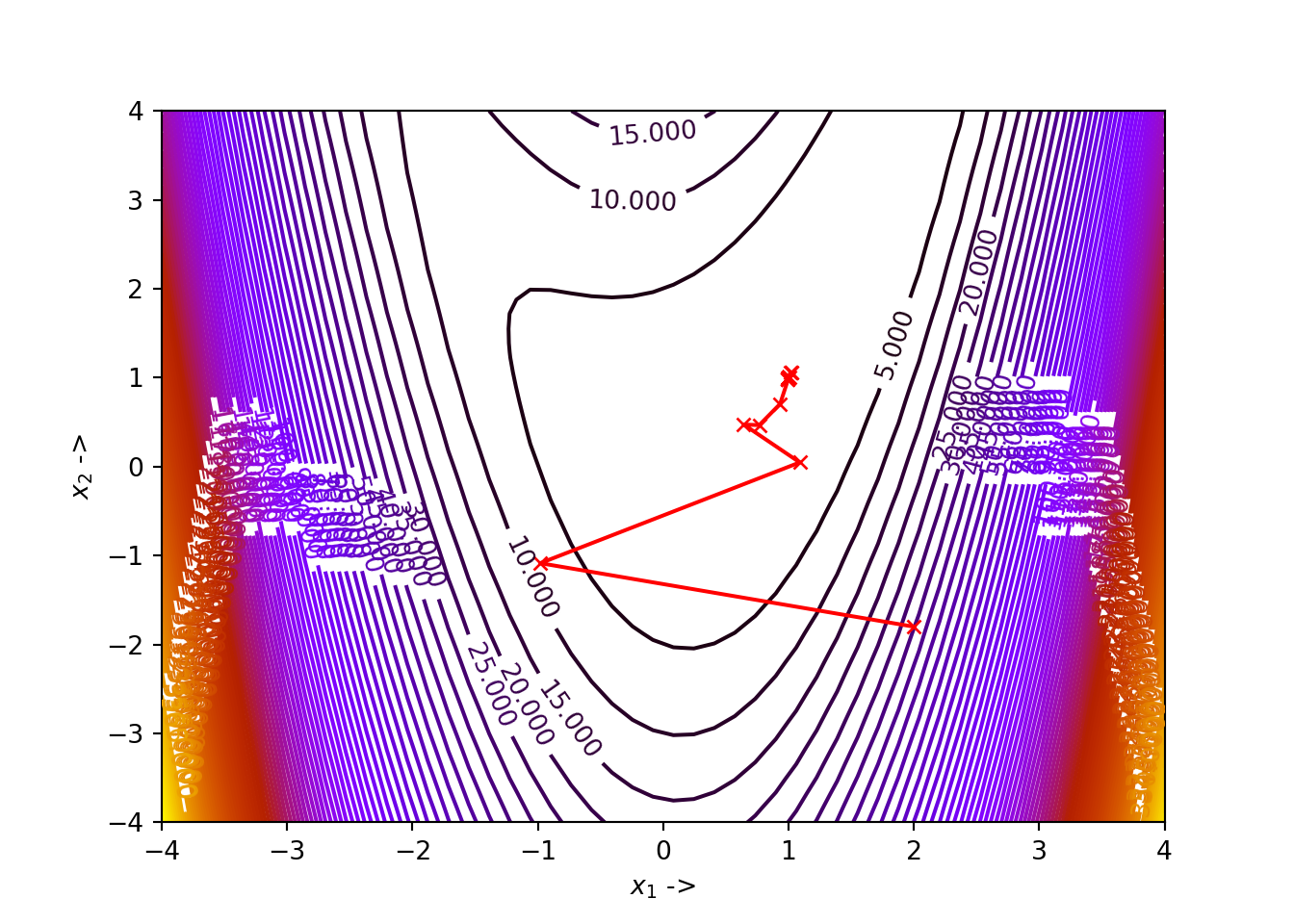
简述 共轭梯度法是利用目标函数的梯度逐步产生共轭方向并将其作为搜索方向的方法。 共轭梯度法是针对二次函数 f ( x ) = 1 2 x T Q x + b T x + c , x ∈ R n f(x)=\frac{1}{2}x^TQx+b^Tx+c,x \in R^n f(x)=21xTQx+bTx+c,x∈Rn 的无约束优化问题。此方法具有存储变量少和收敛速度快的特点。 共轭方向 设共
共轭复数,共轭根式,共轭矩阵,共轭方向,共轭方向法,共轭梯度法,共轭分布,共轭函数,傅里叶变换的共轭对称
目录 1. 共轭复数 2. 傅里叶变换的共轭对称性 3. 共轭根式(radical conjugates) 4. 共轭矩阵(自共轭矩阵、Hermitian(埃尔米特)矩阵) 5. 共轭方向 6. 共轭方向法 7. 共轭梯度法 8. 共轭分布(conjugacy) 9. 共轭函数(对偶函数、极化函数) 共轭(conjugate )的概念在数学、物理、化学、地理等学科中都有出现
e^{ix} 的 conjugate value(复共轭)
e^{ix} 的 conjugate value 正文实数的复共轭 e i x e^{ix} eix 的复共轭推导 正文 这里简单说明一下 e i x e^{ix} eix 的复共轭。 实数的复共轭 首先,我们知道,所谓复共轭是针对复数而言的。对于实数,我们知道,实数集被复数集包含。因此,实数也可以看作是一个复数,比如,对于实数 x x x,其复数形式为: x +
hdu 4565 So Easy!(矩阵乘法+共轭公式)
Problem Description A sequence Sn is defined as: Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate Sn. You, a top coder, say: So easy!
先验概率 后验概率 似然 极大似然估计 极大后验估计 共轭 概念
http://blog.csdn.net/hxxiaopei/article/details/8034184 最近在看LDA,里面涉及到 狄利克雷的概念,为了把这个事情搞明白,查了一些相关概率知识, 举个例子,掷硬币,伯努利实验 中随机变量x={正面,背面},正面的概率μ为模型参数,假定做了N次试验,Data 中观察序列为X={正面,正面。。。。反面},正面的次数为k,服从二项分布:p(
复数矩阵的转置、共轭、共轭转置
复数矩阵的转置分【共轭转置】和【点转置】两种,如果不加说明默认指的是【共轭转置】。 在 MATLAB 中,点转置运算、共轭运算和共轭转置运算分别如下所示:
共轭梯度法、 最速下降法求解大规模稀疏方程组【Matlab】
针对此题,可分别用共轭梯度法、 最速下降法求解线性方程组。 程序如下: 附录1 共辄梯度法求解大规模稀疏方程组程序 附录2 三对角矩阵A、右端项b生成程序 附录3 最速下降法求解线性方程组程序 % 附录1 共轭梯度法求解大规模稀疏方程组程序%% 利用共轭梯度法求解大规模稀疏方程组clear %清除变量clc %清除命令行窗口代码aa
Hdu 4565 So Easy! 矩阵快速幂+共轭数
So Easy! Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 4352 Accepted Submission(s): 1421 Problem Description A sequence S n is
【STM32F429的DSP教程】第19章 DSP复数运算-共轭,点乘和求模
完整版教程下载地址:http://www.armbbs.cn/forum.php?mod=viewthread&tid=94547 第19章 DSP复数运算-共轭,点乘和求模 本期教程主要讲解复数运算中的共轭,点乘和模的求解。 目录 第19章 DSP复数运算-共轭,点乘和求模 19.1 初学者重要提示 19.2 DSP基础运算指令 19.3 复数共轭运算(Co
【STM32F407的DSP教程】第19章 DSP复数运算-共轭,点乘和求模
完整版教程下载地址:http://www.armbbs.cn/forum.php?mod=viewthread&tid=94547 第19章 DSP复数运算-共轭,点乘和求模 本期教程主要讲解复数运算中的共轭,点乘和模的求解。 目录 第19章 DSP复数运算-共轭,点乘和求模 19.1 初学者重要提示 19.2 DSP基础运算指令 19.3 复数共轭运算(Co
浅聊反射系数——为何有共轭?
文章目录 1、基于行波理论的行波反射系数2、共轭匹配与功率波反射系数3、总结 不知道大家是否有和我一样,有下列疑惑:为什么反射系数定义中分子有的时候存在共轭,有的时候又没有共轭。比如: 通俗解释就是:一般来说,Z 0代表传输线的特性阻抗——为实数。所以多数时候,定义为右边的表达式;当Z 0为虚数时,就必须采用左边的定义式了。 不深究的话,一般来说到这里,回答也就
根轨迹关于实轴对称的证明及实系数多项式共轭求解
文章目录 根轨迹关于实轴对称的证明引理1.代数学基本定理引理2.二次实系数多项式的共轭3.证明过程 根轨迹关于实轴对称的证明 引理1.代数学基本定理 任何复系数一元n次多项式 方程在复数域上至少有一根(n≥1),由此推出,n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算) p ( x ) = a n ( x − z 1 ) ( x − z 2 ) ( x −
Matlab观察预处理共轭梯度法(PCG)效果
文章目录 题目程序运行实例结论 题目 题目来自高等数值分析作业题: 程序 随机给b的取值,可以改成指定,由于这几种预处理方法条件数改变不多,b的随机性会导致结果相差较大。 clcclearn=100; %生成矩阵阶数A = hilb(n); %生成hilb矩阵con_A=cond(A); %计算条件数b=rand(n,1); %方式一:生成随机矩阵作为y% fo
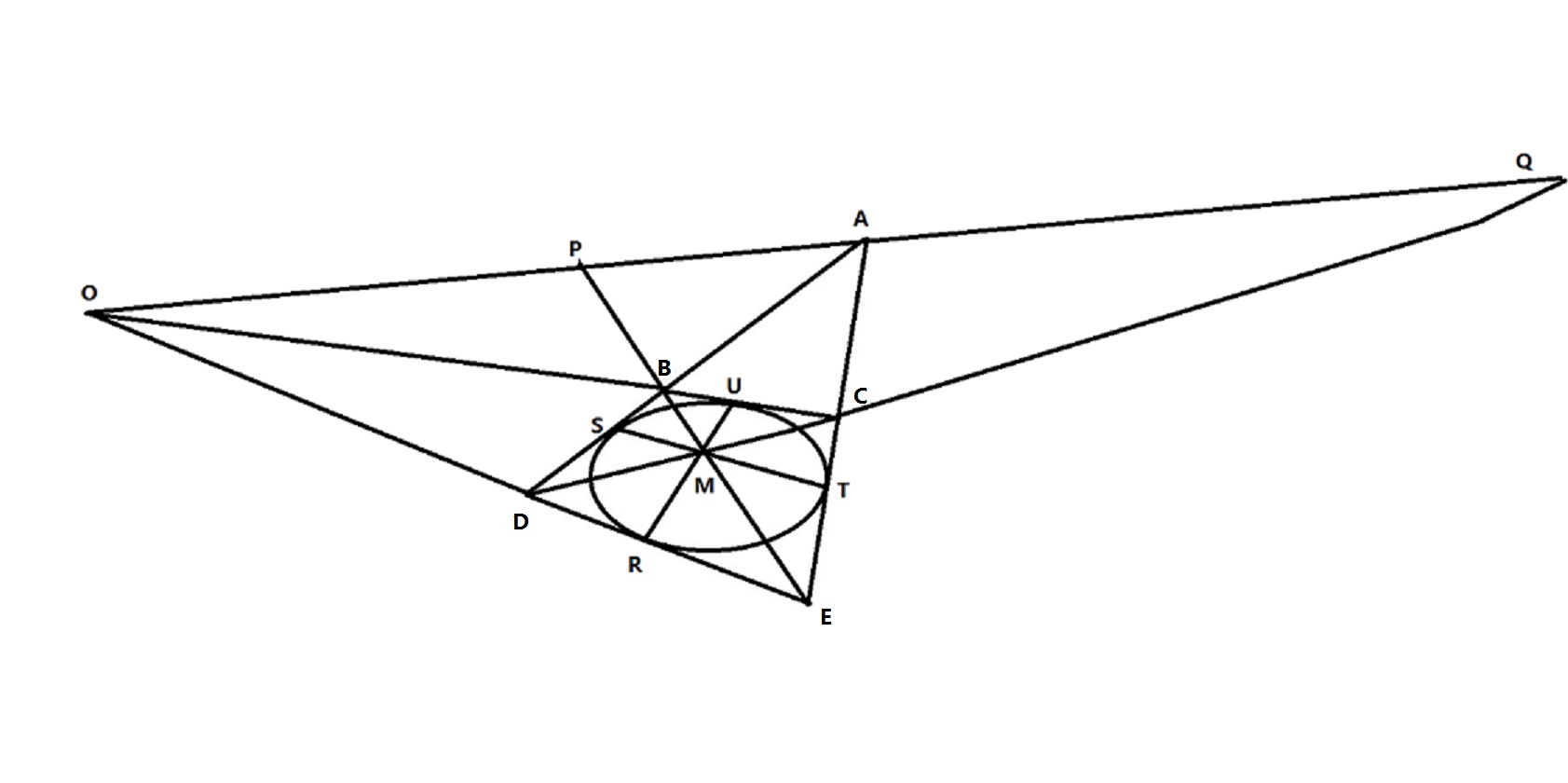
射影几何----三角形外切于一条二次曲线则任一顶点的共轭点与另两点的连线共轭【原创共轭点共轭线定理】
证明: 连接RM并延长RM和曲线交于点U 过U点做曲线的切线交AB和AC与点D和E RS和UT交于一点P,RT和SU交于一点Q 则曲线的外切四边形DECB为曲线的完全四线形 D与C,B与E,O与A为三对对顶点 CD与BE与OA围成的三角形PQM为自极三线形 所以PM和QM共轭 既是CM和BM共轭 命题得证。
射影几何----内接于一二次曲线的三角形中,任一边的共轭线与另两边交于一对共轭点【原创--共轭点共轭线定理】
如图三角形ABC是二次曲线的一个内接三角形 AB与CD的交点为X AC与BC的交点为Y AD与BC的交点为M B点的切线和C点的切线交于点S,根据著名的帕斯卡定理S在XY上 XY是BC的共轭直线,因为XY的极点为M,BC的极点为S 所以XMY为二次曲线的自极三点形,Y点的极线为XM 所以X为Y点的共轭点。
射影几何----共轭点共轭线逆定理--内接与一二次曲线的三角形中,与它的两边交于一对共轭点的直线是第三边的共轭线
内接与一二次曲线的三角形中,与它的两边交于一对共轭点的直线是第三边的共轭线