预条件共轭梯度下降法PCG浅谈

简介

共轭梯度法是一种求解SPD系统线性方程组的迭代方法。它本来是一种直接法，但是通过迭代法求解后，配合复杂的预条件方法，反而更受欢迎。

我们将求解

转化为求解phi(x) 的最小值

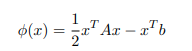
注意：A的SPD性质确保了它的唯一性。

线性搜索法

将线性求解的问题转化为求最小值的问题后，我们尝试用线性求解的方式。我们首先选择一个初始位置，不同的方法会选择不同的方向和step length。

其中，local gradient经过计算就是，这个也会被称为系统残差。

对应的步长如下

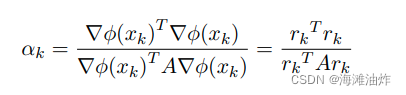
 但是我们认为最速梯度下降法zigzag的路线并不能真正最快的找到最优解，因此想到了利用历史梯度的先验信息去解决这个问题。

共轭梯度下降法

共轭梯度法利用N个相互独立并且共轭的向量，我们可以把从初值得到方程解。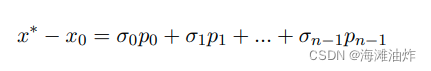

 但是，如何得到这n个共轭梯度呢？

思路一：采用特征向量，但是，特征向量的求解也需要大量计算。

思路二：Gram-Schmidt orthogonalization process, 它需要存储所有的方向。

思路三： 我们想要借助之前的方向和当前的最速梯度。

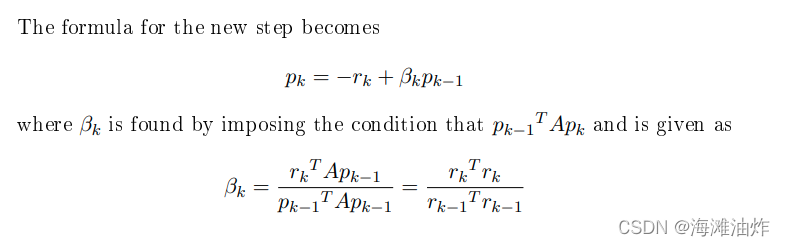
终止条件：当误差小于一个域值的时候，就应该停止搜索。 

预条件

共轭梯度法很好，因为它快，而且容易实现，但是，它的运算复杂度存在很大的随机性，需要的迭代数存在很大的不确定性。

我们想找到一个矩阵和A相乘来让求解具备更好的条件，但是预条件矩阵的求得并不容易。。。

代码实现

代码实现参考了贺博在手写VIO代码中的PCG策略，但是。。。目前我的实现还是存在求解不收敛的情况。欢迎大家指正。

def PCG(A, b,showplot = False):matA= np.array(A)vecb = np.array(b).reshape(-1,1)maxIter = np.shape(vecb)[0]varNum = np.shape(A)[1]x = np.zeros_like(b)r0 = vecberror_hist =[]if (np.linalg.norm(r0)<1e-6):return x# calculate preconditionM_inv_diag = (1.0/np.diag(matA)).reshape(-1,1);for num in M_inv_diag:if (np.isinf(num)):num = 0#print("M_inv_diag ",M_inv_diag)z0 = np.multiply(M_inv_diag , r0)#取得第一个基底，计算基底权重 alpha，并更新 xp = z0w = A @ pr0z0 = r0.T@z0#print("r0z0 ",r0z0)alpha = r0z0/(p.T@w)# print("alpha ",alpha)# print("p ",p)x += alpha *pr1 = r0 - alpha * w#设定迭代终止的阈值threshold = 1e-6 * np.linalg.norm(r0)i = 0while(np.linalg.norm(r1)>threshold and i < maxIter):error_hist.append(float(np.linalg.norm(r1))/varNum)i+= 1z1 = np.multiply(M_inv_diag,r1)r1z1 = r1.T@z1beta = r1z1/r0z0z0 =z1r0z0 = r1z1r0 = r1p = beta * p +z1w = A @ palpha = r1z1/(p.T@w)x += alpha * pr1 -= alpha*wprint("error list",error_hist)plt.plot(error_hist)return xdef testPCG(rows,cols):if(rows<cols):print("nullspace exists")returnA = np.random.rand(rows,cols)x = np.random.rand(cols,1)*10b = A@xprint("A: ",A)print("x: ",x)print("b: ",b)res = PCG(A,b, True)print("res ",res)return testPCG(5,5)

参考资料：

共轭梯度简明文档：https://folk.idi.ntnu.no/elster/tdt24/tdt24-f09/cg.pdf
PCG 伪代码参考文档：https://www.cse.psu.edu/~b58/cse456/lecture20.pdf